Как интерпретировать изогнутый график остатков (с примером)
Графики остатков используются для оценки того, нормально ли распределяются остатки регрессионной модели и проявляют ли они гетероскедастичность .
В идеале вы хотели бы, чтобы точки на остаточном графике были случайным образом разбросаны вокруг нулевого значения без четкой закономерности.
Если вы столкнулись с остаточным графиком, на котором точки графика имеют изогнутую форму, это, вероятно, означает, что модель регрессии, которую вы указали для данных, неверна.
В большинстве случаев это означает, что вы попытались подогнать модель линейной регрессии к набору данных, который вместо этого следует квадратичному тренду.
В следующем примере показано, как на практике интерпретировать (и корректировать) изогнутый график остатков.
Пример: Интерпретация изогнутого графика остатков
Предположим, мы собираем следующие данные о количестве отработанных часов в неделю и заявленном уровне счастья (по шкале от 0 до 100) для 11 разных людей в офисе:

Если бы мы создали простую диаграмму отработанных часов в зависимости от уровня счастья, она бы выглядела следующим образом:
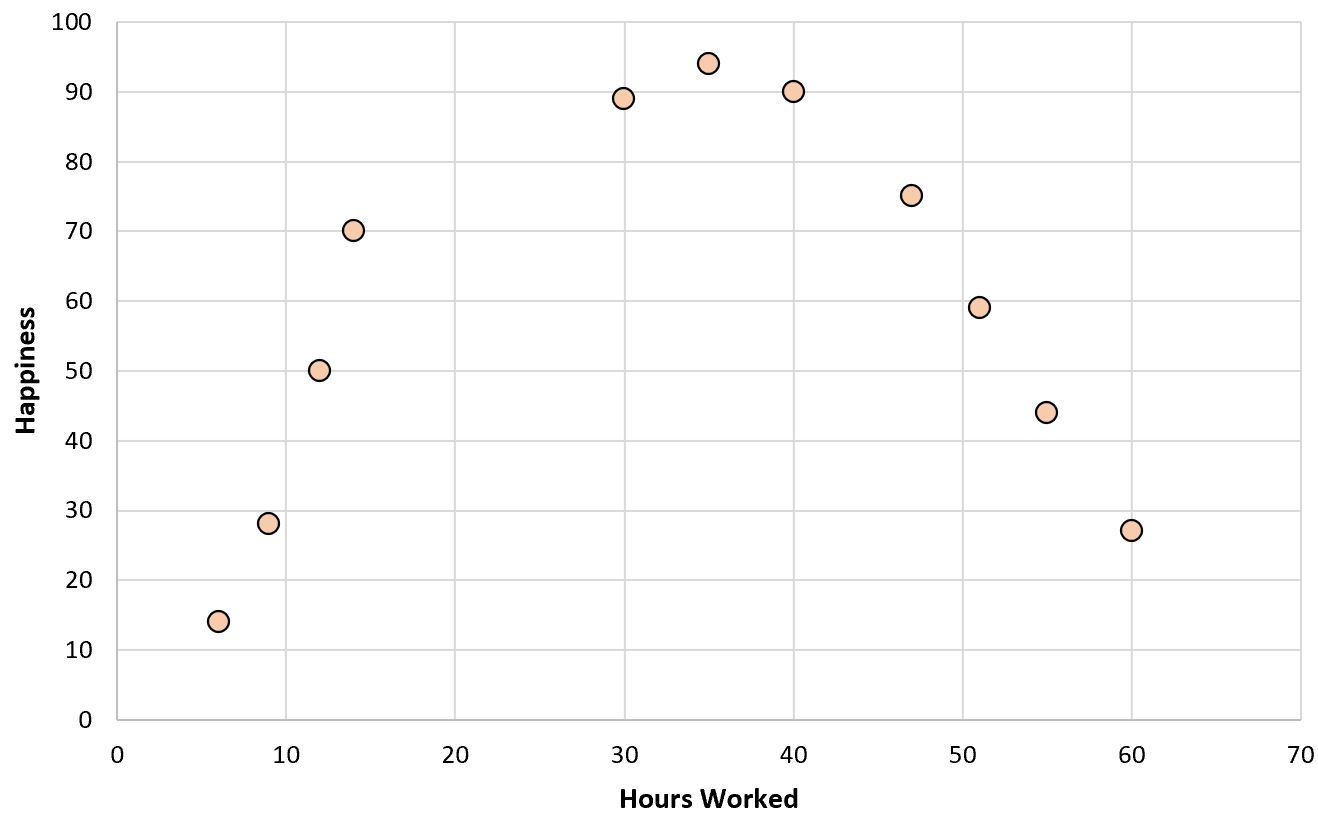
Теперь предположим, что мы хотим подогнать регрессионную модель, используя отработанное время, для прогнозирования уровня счастья.
Следующий код показывает, как подогнать простую модель линейной регрессии к этому набору данных и построить остаточный график в R:
#create dataframe
df <- data. frame (hours=c(6, 9, 12, 14, 30, 35, 40, 47, 51, 55, 60),
happiness=c(14, 28, 50, 70, 89, 94, 90, 75, 59, 44, 27))
#fit linear regression model
linear_model <- lm(happiness ~ hours, data=df)
#get list of residuals
res <- resid(linear_model)
#produce residual vs. fitted plot
plot(fitted(linear_model), res, xlab=' Fitted Values ', ylab=' Residuals ')
#add a horizontal line at 0
abline(0,0)
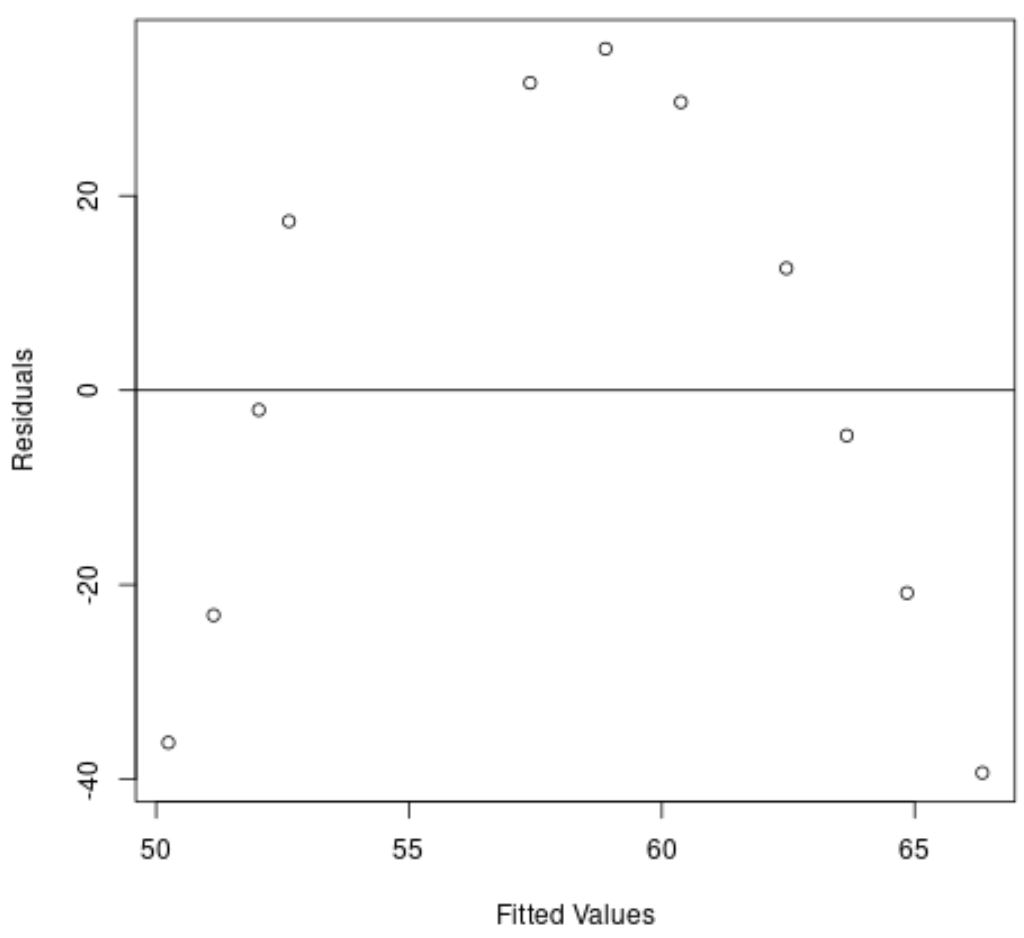
По оси X отображаются подобранные значения, а по оси Y — остатки.
На графике мы видим, что остатки имеют изогнутую структуру, что указывает на то, что модель линейной регрессии не обеспечивает подходящего соответствия этому набору данных.
Следующий код показывает, как подогнать модель квадратичной регрессии к этому набору данных и построить остаточный график в R:
#create dataframe
df <- data. frame (hours=c(6, 9, 12, 14, 30, 35, 40, 47, 51, 55, 60),
happiness=c(14, 28, 50, 70, 89, 94, 90, 75, 59, 44, 27))
#define quadratic term to use in model
df$hours2 <- df$hours^2
#fit quadratic regression model
quadratic_model <- lm(happiness ~ hours + hours2, data=df)
#get list of residuals
res <- resid(quadratic_model)
#produce residual vs. fitted plot
plot(fitted(quadratic_model), res, xlab=' Fitted Values ', ylab=' Residuals ')
#add a horizontal line at 0
abline(0,0)
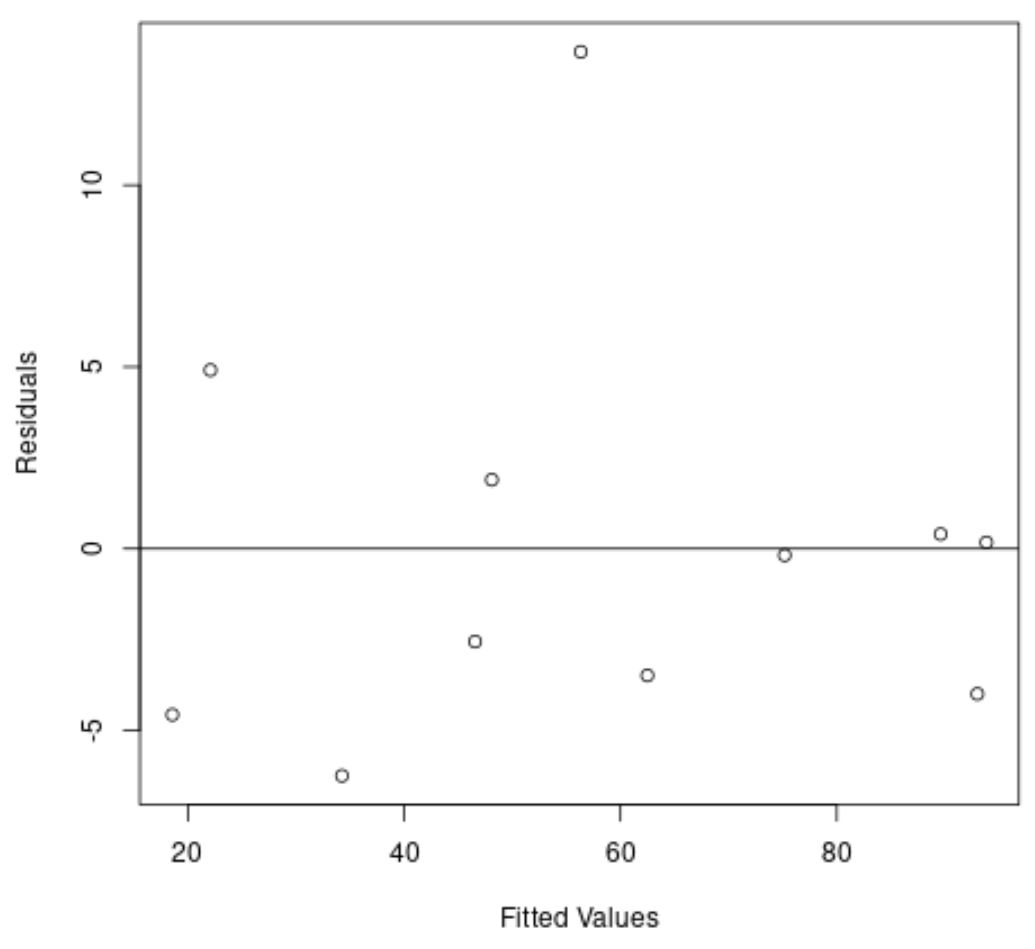
Еще раз: ось X показывает подобранные значения, а ось Y показывает остатки.
На графике мы видим, что остатки случайным образом разбросаны вокруг нуля, и в остатках нет четкой тенденции.
Это говорит нам о том, что модель квадратичной регрессии гораздо лучше подходит для этого набора данных, чем модель линейной регрессии.
Это должно иметь смысл, учитывая, что мы видели, что истинная связь между отработанным временем и уровнем счастья оказалась квадратичной, а не линейной.
Дополнительные ресурсы
В следующих руководствах объясняется, как создавать графики остатков с использованием различного статистического программного обеспечения:
Как создать остаточный путь вручную
Как создать остаточный график в R
Как создать остаточный график в Excel
Как создать остаточный график в Python