Индекс джини (или коэффициент джини)
В этой статье объясняется, что такое индекс Джини, также называемый коэффициентом Джини, и для чего он используется. Кроме того, вы найдете решенное упражнение о том, как найти индекс Джини. Наконец, вы сможете увидеть интерпретацию этого статистического показателя и то, какова связь между индексом Джини и кривой Лоренца.
Что такое индекс Джини?
Индекс Джини , также называемый коэффициентом Джини , представляет собой статистическую величину, используемую для измерения неравенства доходов на территории. Другими словами, индекс Джини показывает, насколько территория равномерно распределяет доходы среди своего населения.
Индекс Джини представляет собой число от 0 до 1. Если индекс Джини равен 0, это означает, что распределение доходов на территории максимально справедливое (совершенное равенство), или, другими словами, все жители имеют одинаковый доход. С другой стороны, когда коэффициент Джини равен 1, это соответствует совершенному неравенству, то есть один человек получает весь доход территории, а остальные ничего не получают.
Индекс Джини используется для сравнения экономической ситуации между разными странами мира, поскольку он позволяет сравнивать наиболее эгалитарные страны и, наоборот, наиболее неравные страны с точки зрения распределения доходов.
Индекс Джини был изобретен известным статистиком Коррадо Джини, отсюда и его название.
Как рассчитать индекс Джини
Учитывая определение индекса Джини (или коэффициента Джини), вот как рассчитывается этот статистический показатель.
Формула индекса Джини (или коэффициента Джини) выглядит следующим образом:
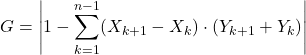
Золото:
-
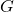
это индекс Джини.
-

представляет собой совокупную долю переменной совокупности.
-
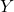
– совокупная доля переменной дохода.
Чтобы вы могли увидеть, как именно определяется индекс Джини, ниже решен пошаговый пример:
- Рассчитайте индекс Джини для населения, доходы которого показаны в следующей таблице.
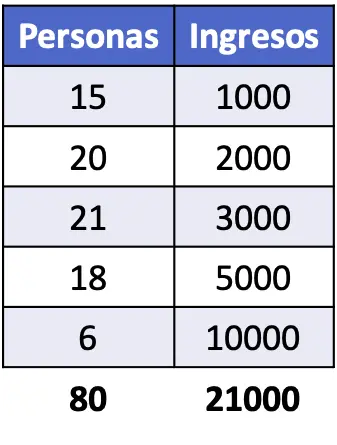
Чтобы найти коэффициент Джини, нам необходимо определить долю каждого уровня дохода, а также совокупную долю. Дополнительно для нахождения значения индекса Джини необходимо выполнить приведенные в формуле расчеты.
Короче говоря, в таблицу данных следует добавить следующие столбцы:
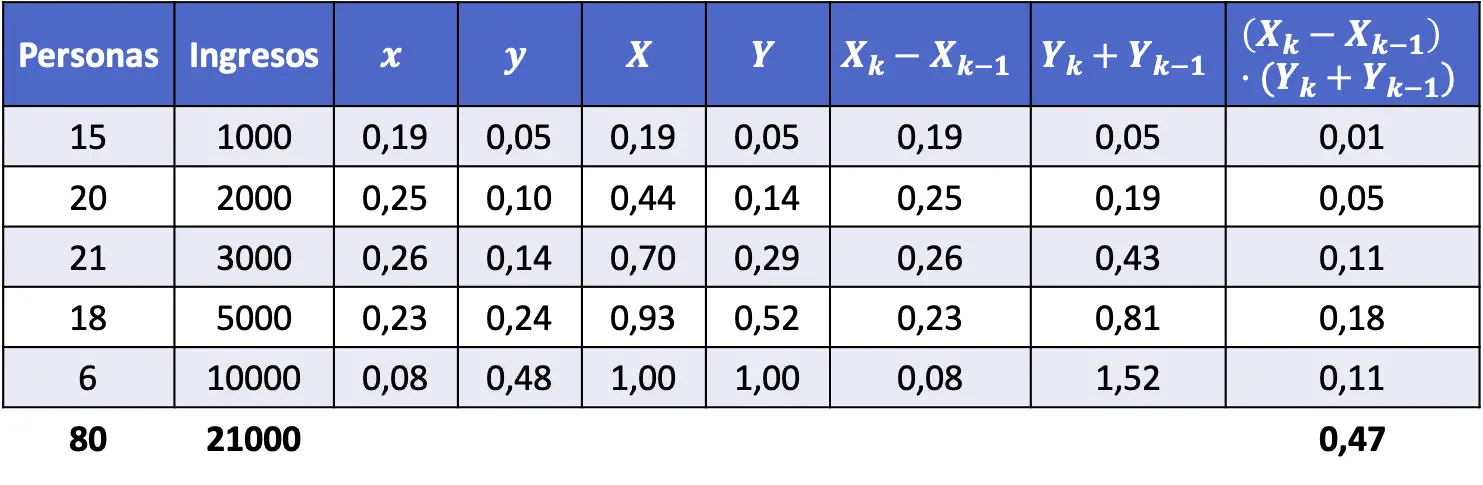
Теперь мы используем формулу индекса Джини:
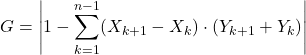
И наконец, подставляем данные в алгебраическое выражение и вычисляем коэффициент Джини:
![]()
Связь между индексом Джини и кривой Лоренца
В этом разделе мы увидим, как связаны индекс Джини, также известный как коэффициент Джини, и кривая Лоренца.
Кривая Лоренца — это графическое изображение экономического неравенства населения территории. Таким образом, кривая Лоренца наглядно указывает на экономическое неравенство населения.
С другой стороны, как мы видели, индекс Джини — это величина, используемая для численного описания неравенства населения.
Таким образом, индекс Джини и кривая Лоренца преследуют одну и ту же цель : оба используются для определения экономического неравенства между жителями территории. Однако индекс Джини оценивает неравенство доходов численно, а кривая Лоренца анализирует экономическое неравенство графически.
Кроме того, индекс Джини можно рассчитать по площадям, ограниченным кривой Лоренца, по следующей формуле:
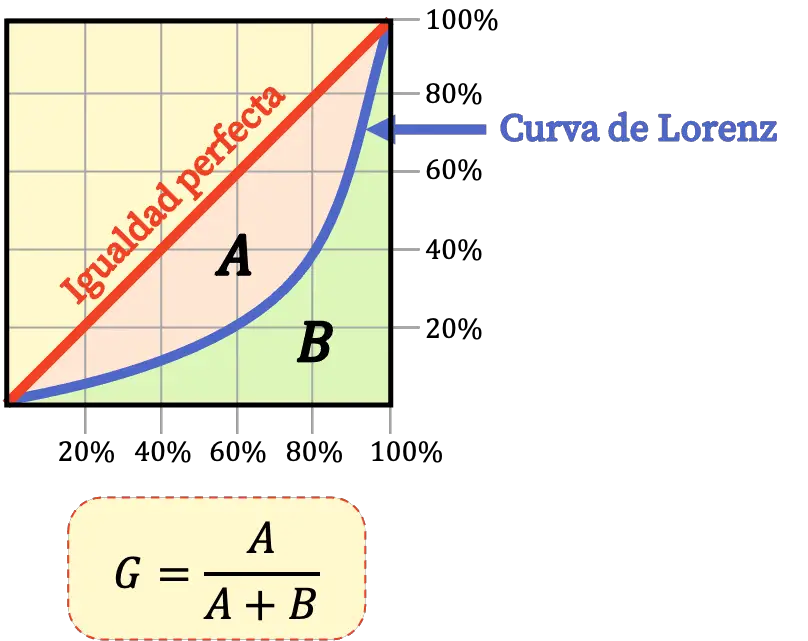
Интерпретация индекса Джини
Значение индекса Джини может варьироваться от 0 до 1 включительно. Чем ближе значение коэффициента Джини к 0, это означает, что на территории больше экономического равенства. С другой стороны, чем выше значение индекса Джини, тем больше неравенство в распределении доходов между жителями территории.
Таким образом, индекс Джини будет равен нулю в оптимальной ситуации, когда все жители имеют одинаковый доход. Напротив, индекс Джини будет равен 1, когда на территории наблюдается совершенное неравенство, то есть один житель получает весь доход, а остальные жители не имеют дохода.
Таким образом, страны с более высоким равенством доходов — это страны с более низким индексом Джини. А страны с самым высоким уровнем неравенства имеют очень высокий индекс Джини.
Как мы видели, индекс Джини связан с кривой Лоренца. Таким образом, чем ниже индекс Джини, тем ближе кривая Лоренца будет к линии совершенного равенства. Чем выше индекс Джини, тем большую кривизну будет иметь кривая Джини и, следовательно, тем дальше она будет от линии, представляющей идеальное равенство.