Полное руководство: как интерпретировать результаты anova в excel

Однофакторный дисперсионный анализ используется для определения наличия или отсутствия статистически значимой разницы между средними значениями трех или более независимых групп.

В следующем примере представлено полное руководство по интерпретации результатов однофакторного дисперсионного анализа в Excel.

Пример: Как интерпретировать результаты ANOVA в Excel

Предположим, учитель случайным образом просит 30 учеников своего класса использовать один из трех методов обучения для подготовки к экзамену.

На следующем снимке экрана показаны оценки учащихся в зависимости от использованного ими метода:

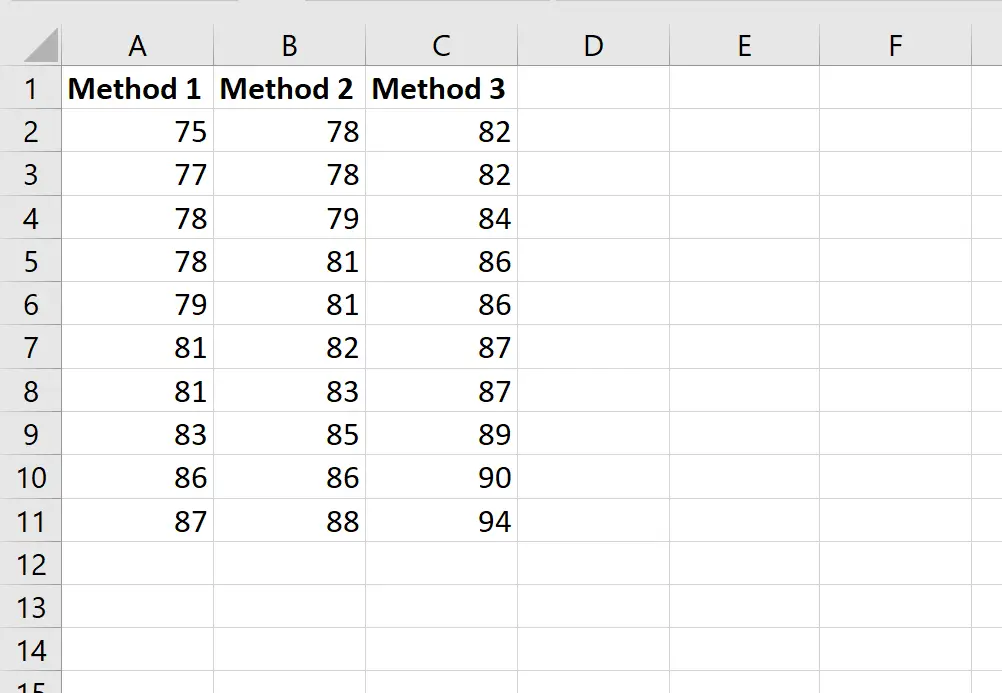
Предположим, учитель хочет выполнить однофакторный дисперсионный анализ, чтобы определить, одинаковы ли средние баллы в трех группах.

Чтобы выполнить однофакторный дисперсионный анализ в Excel, щелкните вкладку «Данные» на верхней ленте, а затем нажмите «Анализ данных» в группе «Анализ» .

Если вы не видите параметр «Анализ данных » , сначала необходимо загрузить бесплатное программное обеспечение Analysis ToolPak .

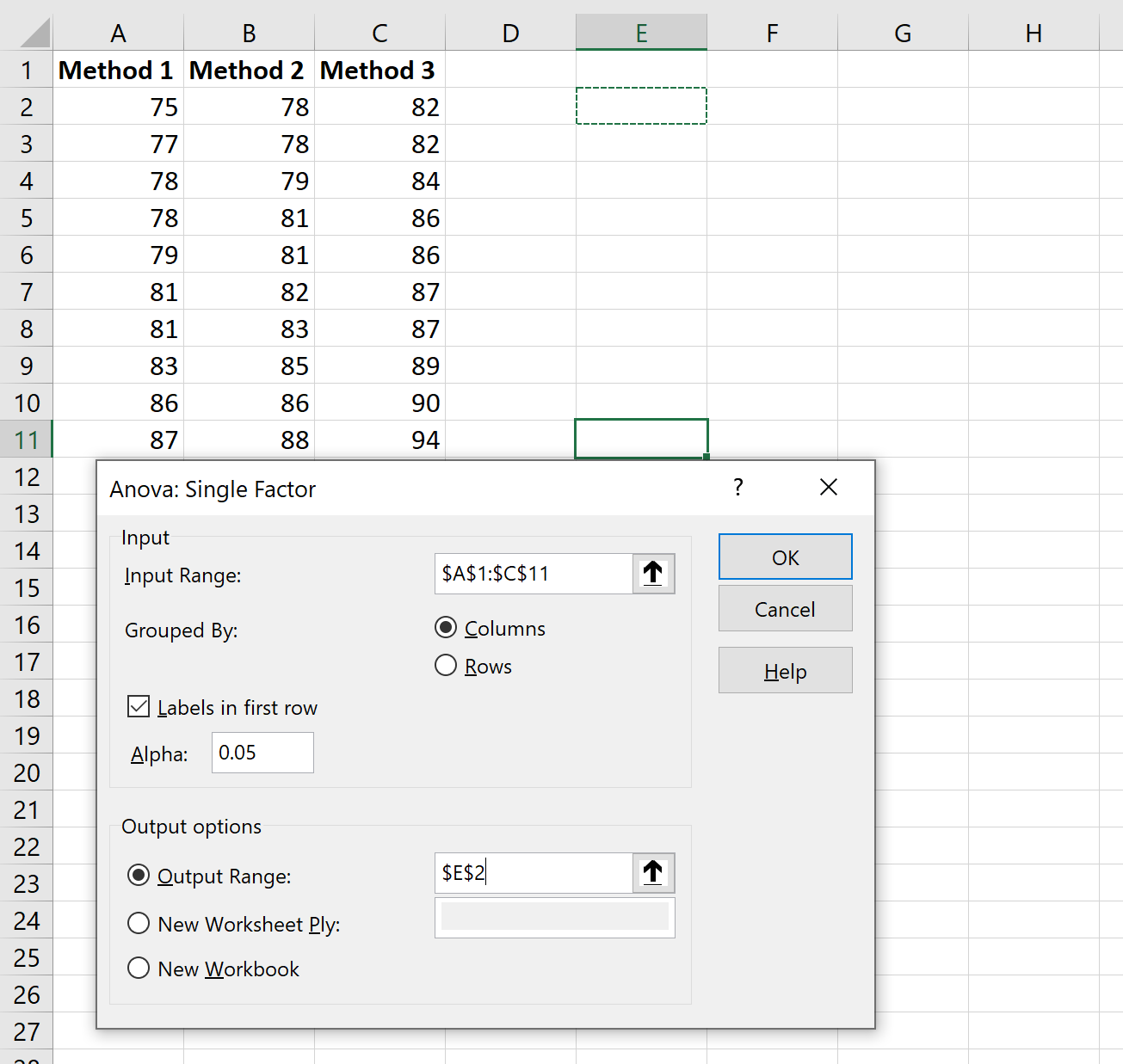
Как только вы нажмете на нее, появится новое окно. Выберите Anova: Single Factor и нажмите OK .

В появившемся новом окне введите следующую информацию:

Как только вы нажмете «ОК» , появятся результаты одностороннего дисперсионного анализа:

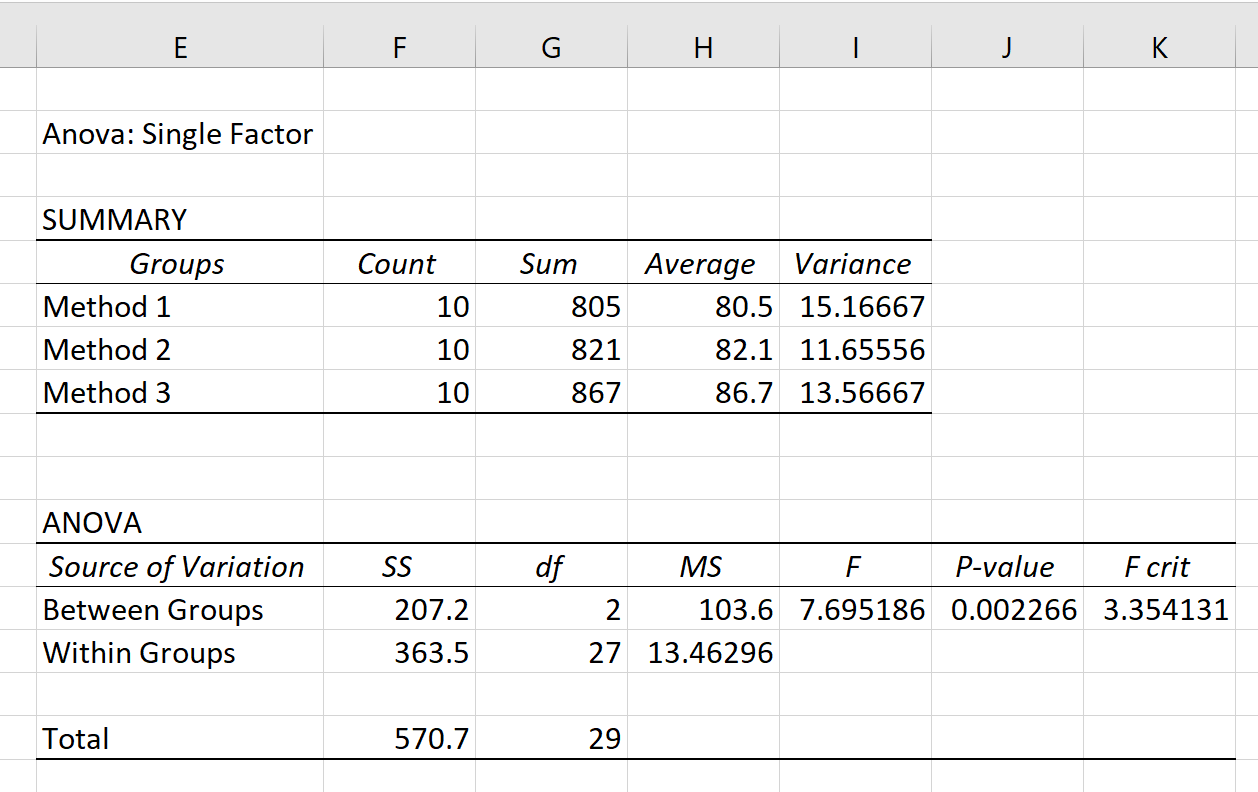
В результате отображаются две таблицы: SUMMARY и ANOVA .

Вот как интерпретировать значения в каждой таблице:

СВОДНАЯ таблица :

• Группы : названия групп.
• Подсчет : количество наблюдений в каждой группе.
• Сумма : сумма значений каждой группы.
• Среднее : среднее значение в каждой группе.
• Разница : разница значений в каждой группе.

Эта таблица предоставляет нам несколько полезных сводных статистических данных для каждой группы, используемой в ANOVA.

Из этой таблицы мы видим, что студенты, использовавшие метод 3, имели самый высокий средний балл на экзамене (86,7), но у них также была самая большая разница в результатах тестов. обзор (13.56667).

Чтобы определить, являются ли различия в групповых средних статистически значимыми, мы должны обратиться к таблице ANOVA.

Таблица дисперсионного анализа :

• Источник вариаций : измеренная вариация (между группами или внутри групп).
• SS : сумма квадратов для каждого источника вариаций.
• df : Степени свободы, рассчитанные как #groups-1 для df Между и #observations – #groups для df Внутри.
• MS : средняя сумма квадратов, рассчитанная в SS/df.
• F : общее значение F, рассчитанное как MS Между / MS Внутри.
• P-значение : P-значение, соответствующее общему F-значению.
• F crit : критическое значение F, соответствующее α = 0,05.

Самым важным значением в этой таблице является значение p , которое оказывается равным 0,002266 .

Напомним, что однофакторный дисперсионный анализ использует следующие нулевые и альтернативные гипотезы:

• H ₀ : Все средние значения группы равны.
• _ХА : Не все средние показатели по группам одинаковы.

Поскольку значение p меньше α = 0,05, мы отвергаем нулевую гипотезу одностороннего дисперсионного анализа и приходим к выводу, что у нас есть достаточные доказательства, чтобы утверждать, что все групповые средние не равны.

Это означает, что не все три метода обучения приводят к одинаковым средним оценкам на экзамене.

Примечание . Вы также можете сравнить общее значение F с критическим значением F, чтобы определить, следует ли отвергать нулевую гипотезу. В этом случае, поскольку общее значение F больше критического значения F, мы отвергнем нулевую гипотезу. Обратите внимание, что подход с использованием p-значения и подход с критическим F-значением всегда приводят к одному и тому же выводу.

Дополнительные ресурсы

В следующих руководствах объясняется, как выполнять различные ANOVA в Excel:

Как выполнить однофакторный дисперсионный анализ в Excel
Как выполнить двусторонний дисперсионный анализ в Excel
Как выполнить повторные измерения ANOVA в Excel
Как выполнить вложенный дисперсионный анализ в Excel