Как интерпретировать среднеквадратическую ошибку (rmse)
Регрессионный анализ — это метод, который мы можем использовать, чтобы понять взаимосвязь между одной или несколькими переменными-предикторами и переменной отклика .
Один из способов оценить, насколько хорошо модель регрессии соответствует набору данных, — это вычислить среднеквадратическую ошибку , которая представляет собой метрику, которая сообщает нам среднее расстояние между прогнозируемыми значениями модели и фактическими значениями набора данных.
Чем ниже RMSE, тем лучше данная модель может «подогнать» набор данных.
Формула для нахождения среднеквадратической ошибки, часто обозначаемая сокращенно RMSE , выглядит следующим образом:
RMSE = √ Σ(P i – O i ) 2 / n
Золото:
- Σ — причудливый символ, означающий «сумма».
- Pi — прогнозируемое значение для i-го наблюдения в наборе данных.
- O i — наблюдаемое значение для i-го наблюдения в наборе данных.
- n — размер выборки
В следующем примере показано, как интерпретировать RMSE для данной регрессионной модели.
Пример: Как интерпретировать RMSE для регрессионной модели
Предположим, мы хотим построить регрессионную модель, которая использует «ученые часы» для прогнозирования «экзаменационной оценки» студентов на конкретном вступительном экзамене в колледж.
Мы собираем следующие данные по 15 студентам:
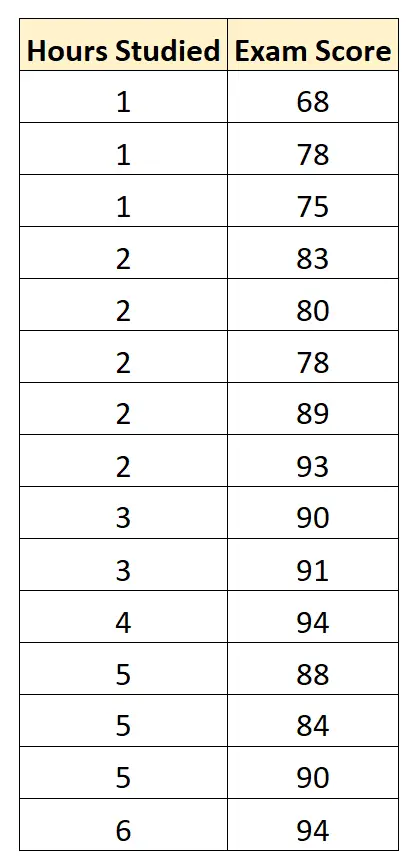
Затем мы используем статистическое программное обеспечение (например, Excel, SPSS, R, Python) и т. д. чтобы найти следующую подобранную регрессионную модель:
Экзаменационный балл = 75,95 + 3,08* (учебные часы)
Затем мы можем использовать это уравнение, чтобы предсказать результат экзамена каждого студента на основе количества часов, которые он проучил:
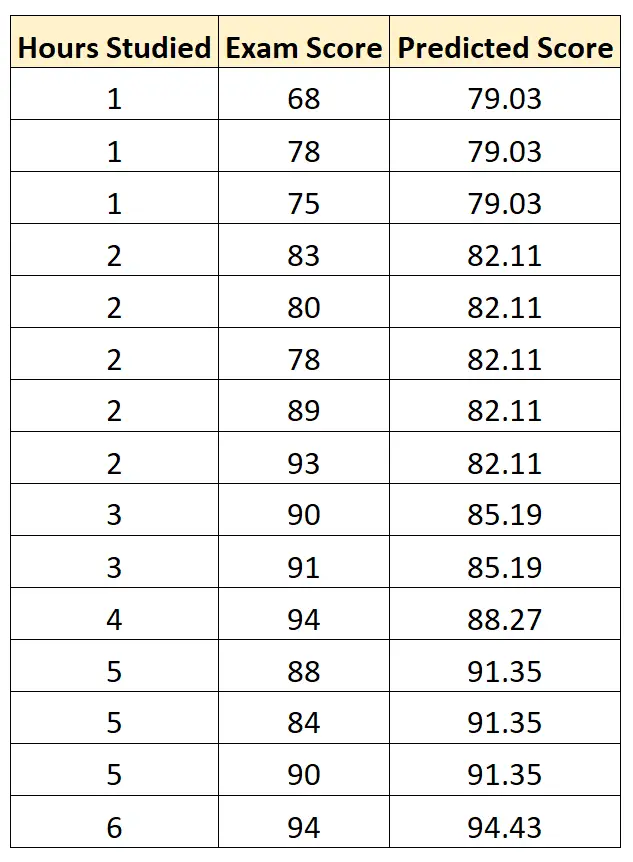
Затем мы можем вычислить квадрат разницы между прогнозируемым результатом экзамена и фактическим баллом экзамена. Затем мы можем извлечь квадратный корень из среднего значения этих разностей:
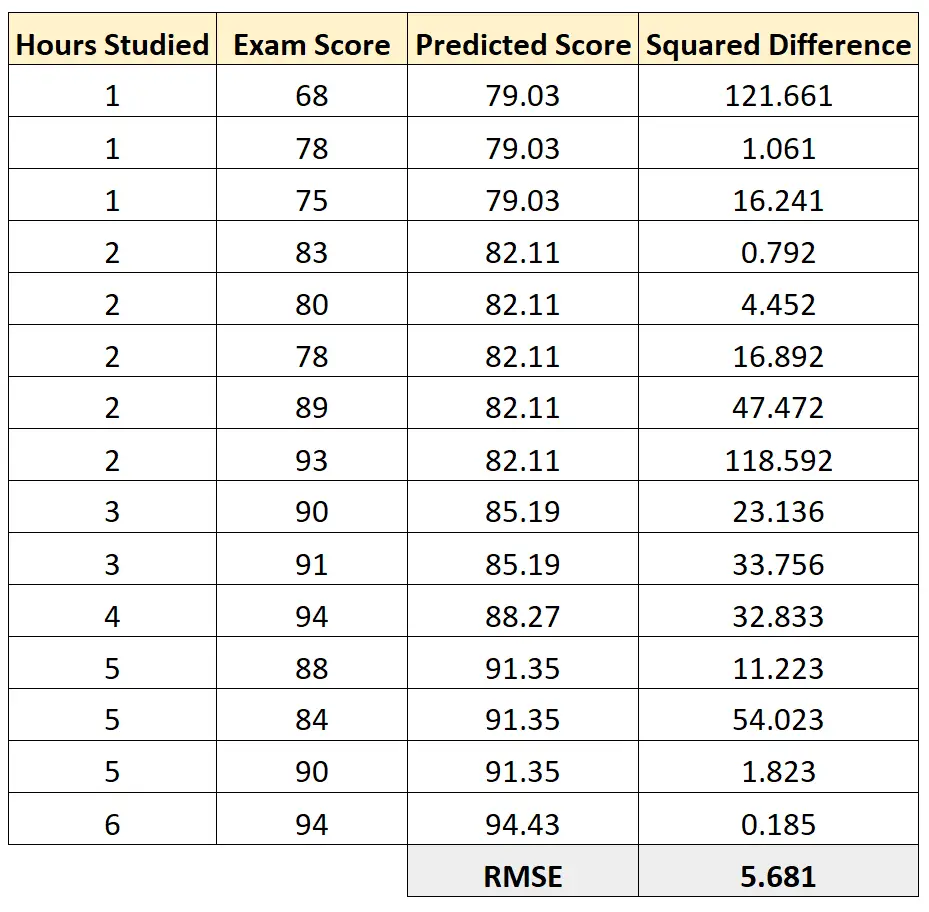
RMSE этой регрессионной модели оказывается равным 5,681 .
Напомним, что остатки регрессионной модели — это разности между наблюдаемыми значениями данных и прогнозируемыми значениями модели.
Остаток = (P i – O i )
Золото
- Pi — прогнозируемое значение для i-го наблюдения в наборе данных.
- O i — наблюдаемое значение для i-го наблюдения в наборе данных.
Помните, что RMSE регрессионной модели рассчитывается следующим образом:
RMSE = √ Σ(P i – O i ) 2 / n
Это означает, что RMSE представляет собой квадратный корень дисперсии остатков.
Это полезное значение, поскольку оно дает нам представление о среднем расстоянии между наблюдаемыми значениями данных и прогнозируемыми значениями данных.
Это контрастирует с R-квадратом модели, который говорит нам, какая часть дисперсии переменной отклика может быть объяснена предикторными переменными модели.
Сравнение значений RMSE разных моделей
RMSE особенно полезен для сравнения соответствия различных моделей регрессии.
Например, предположим, что мы хотим построить регрессионную модель для прогнозирования результатов экзаменов студентов и найти наилучшую возможную модель среди нескольких потенциальных моделей.
Предположим, мы подбираем три разные модели регрессии и находим соответствующие им значения RMSE:
- СКО модели 1: 14,5
- СКО модели 2: 16,7
- СКО модели 3: 9,8
Модель 3 имеет самое низкое среднеквадратическое отклонение, что говорит нам о том, что она лучше всего соответствует набору данных среди трех потенциальных моделей.
Дополнительные ресурсы
Калькулятор RMSE
Как рассчитать RMSE в Excel
Как рассчитать RMSE в R
Как рассчитать RMSE в Python