Как интерпретировать остаточную стандартную ошибку

Остаточная стандартная ошибка используется для измерения того, насколько хорошо модель регрессии соответствует набору данных.

Проще говоря, он измеряет стандартное отклонение остатков в регрессионной модели.

Он рассчитывается следующим образом:

Остаточная стандартная ошибка = √ Σ(y – ŷ) ² /df

Золото:

• y: наблюдаемое значение
• ŷ: прогнозируемое значение
• df: Степени свободы, рассчитанные как общее количество наблюдений – общее количество параметров модели.

Чем меньше остаточная стандартная ошибка, тем лучше модель регрессии соответствует набору данных. И наоборот, чем выше остаточная стандартная ошибка, тем хуже модель регрессии соответствует набору данных.

Модель регрессии с небольшой остаточной стандартной ошибкой будет иметь точки данных, плотно сгруппированные вокруг подобранной линии регрессии:

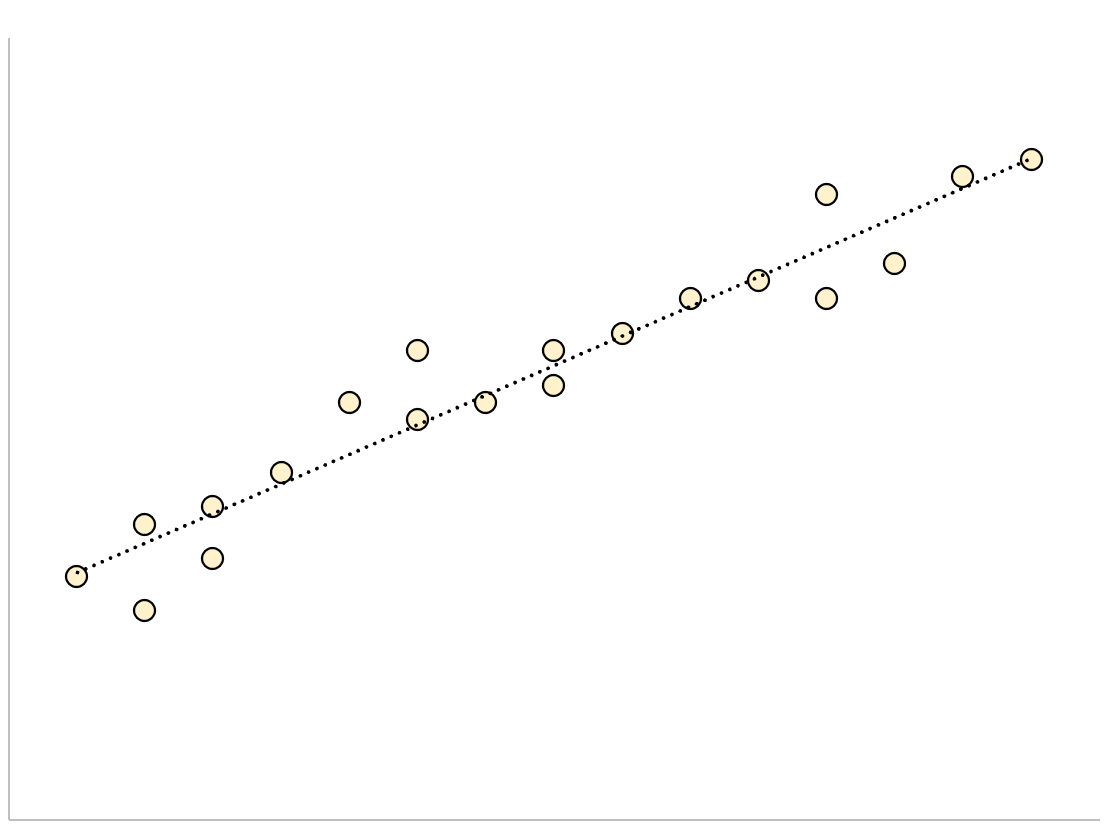
Остатки этой модели (разница между наблюдаемыми значениями и прогнозируемыми значениями) будут небольшими, а это означает, что остаточная стандартная ошибка также будет небольшой.

И наоборот, модель регрессии с большой остаточной стандартной ошибкой будет иметь точки данных, более свободно разбросанные вокруг подобранной линии регрессии:

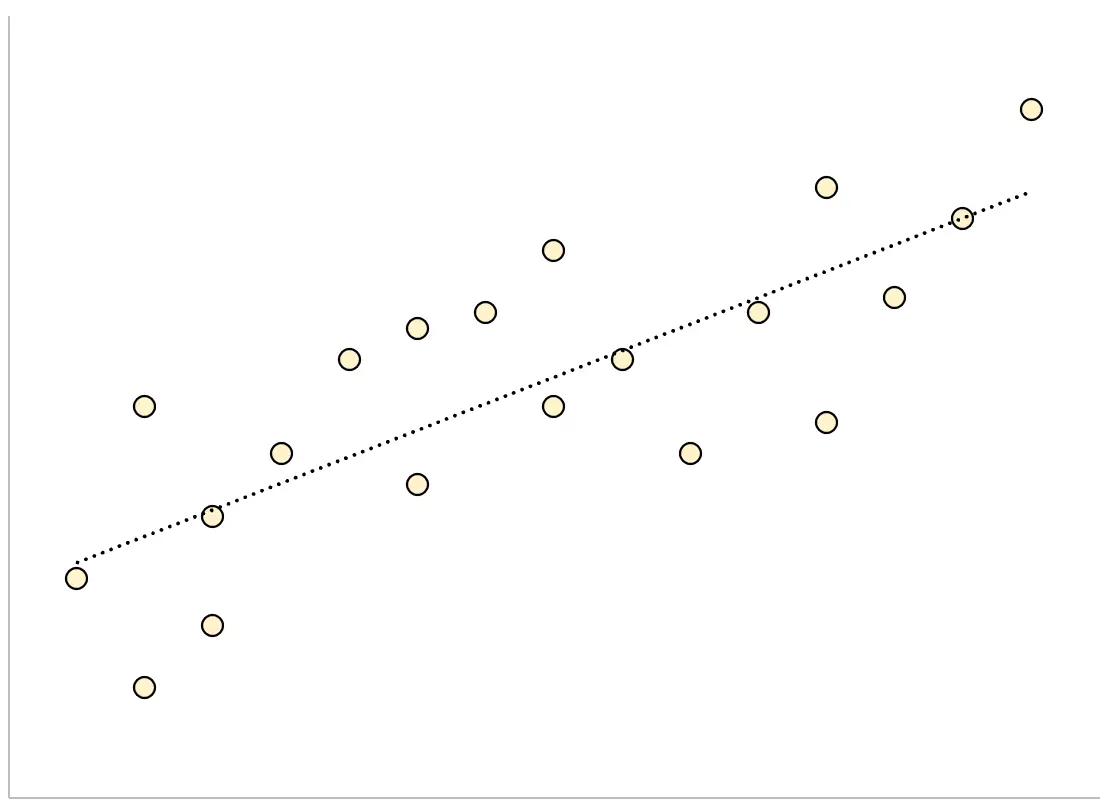
Остатки этой модели будут больше, а это означает, что остаточная стандартная ошибка также будет больше.

В следующем примере показано, как рассчитать и интерпретировать остаточную стандартную ошибку регрессионной модели в R.

Пример: Интерпретация остаточной стандартной ошибки

Предположим, мы хотим подогнать следующую модель множественной линейной регрессии:

миль на галлон = β ₀ + β ₁ (объем) + β ₂ (мощность)

Эта модель использует переменные-предсказатели «объем» и «лошадиная сила» для прогнозирования количества миль на галлон, пройденного данным автомобилем.

Следующий код показывает, как подогнать эту регрессионную модель в R:

 #load built-in mtcars dataset
data(mtcars)

#fit regression model
model <- lm(mpg~disp+hp, data=mtcars)

#view model summary
summary(model)

Call:
lm(formula = mpg ~ disp + hp, data = mtcars)

Residuals:
    Min 1Q Median 3Q Max 
-4.7945 -2.3036 -0.8246 1.8582 6.9363 

Coefficients:
             Estimate Std. Error t value Pr(>|t|)    
(Intercept) 30.735904 1.331566 23.083 < 2nd-16 ***
available -0.030346 0.007405 -4.098 0.000306 ***
hp -0.024840 0.013385 -1.856 0.073679 .  
---
Significant. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

Residual standard error: 3.127 on 29 degrees of freedom
Multiple R-squared: 0.7482, Adjusted R-squared: 0.7309 
F-statistic: 43.09 on 2 and 29 DF, p-value: 2.062e-09

В нижней части результата мы видим, что остаточная стандартная ошибка этой модели равна 3,127 .

Это говорит нам о том, что регрессионная модель предсказывает расход автомобиля на галлон со средней ошибкой около 3127.

Использование остаточной стандартной ошибки для сравнения моделей

Остаточная стандартная ошибка особенно полезна для сравнения соответствия различных моделей регрессии.

Например, предположим, что мы подбираем две разные регрессионные модели для прогнозирования расхода топлива на галлон. Остаточная стандартная ошибка каждой модели выглядит следующим образом:

• Остаточная стандартная ошибка модели 1: 3,127.
• Остаточная стандартная ошибка модели 2: 5,657.

Поскольку Модель 1 имеет более низкую остаточную стандартную ошибку, она лучше соответствует данным, чем Модель 2. Таким образом, мы бы предпочли использовать Модель 1 для прогнозирования расхода миль на галлон автомобиля, поскольку ее прогнозы ближе к наблюдаемым значениям расхода миль на галлон автомобилей.

Дополнительные ресурсы

Как выполнить простую линейную регрессию в R
Как выполнить множественную линейную регрессию в R
Как создать остаточный график в R