Как использовать таблицу z (с примерами)
Таблица z — это таблица, которая сообщает вам, какой процент значений находится ниже определенного показателя z в стандартном нормальном распределении.
Z-показатель просто показывает, на сколько стандартных отклонений отдельное значение данных отклоняется от среднего значения. Он рассчитывается следующим образом:
z-показатель = (x – µ) / σ
Золото:
- x: индивидуальное значение данных
- μ: средний показатель по численности населения
- σ: стандартное отклонение совокупности
В этом уроке показано несколько примеров использования таблицы z.
Пример 1
Баллы на определенном вступительном экзамене в колледж обычно распределяются со средним значением μ = 82 и стандартным отклонением σ = 8. Приблизительно какой процент студентов набирает на экзамене балл ниже 84?
Шаг 1: Найдите z-показатель.
Сначала мы найдем z-показатель, соответствующий баллу на экзамене 84:
z-показатель = (x – μ) / σ = (84 – 82) / 8 = 2/8 = 0,25
Шаг 2. Используйте диаграмму z, чтобы найти процент, соответствующий показателю z.
Далее мы будем искать значение 0,25 в таблице z:

Около 59,87% студентов набирают на этом экзамене балл ниже 84.
Пример 2
Высота растений в определенном саду обычно распределяется со средним значением μ = 26,5 дюймов и стандартным отклонением σ = 2,5 дюймов. Приблизительно какой процент растений имеет высоту более 26 дюймов?
Шаг 1: Найдите z-показатель.
Сначала мы найдем z-показатель, связанный с высотой 26 дюймов.
z-показатель = (x – μ) / σ = (26 – 26,5) / 2,5 = -0,5 / 2,5 = -0,2
Шаг 2. Используйте диаграмму z, чтобы найти процент, соответствующий показателю z.
Далее мы будем искать значение -0,2. в таблице з:
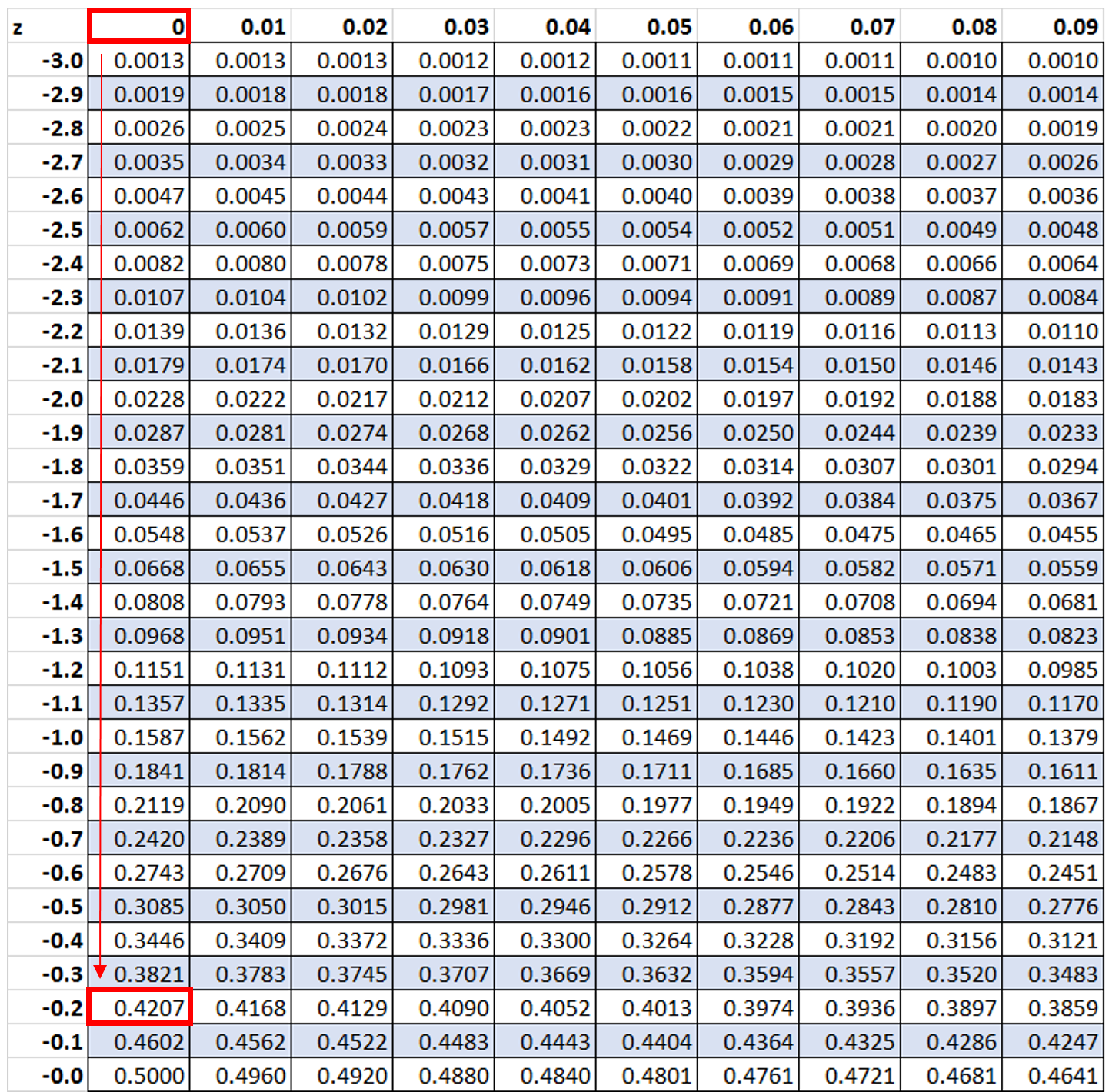
Мы видим, что 42,07% значений находятся ниже z-показателя -0,2. Однако в этом примере мы хотим знать, какой процент значений превышает -0,2, что мы можем найти по формуле 100% – 42,07% = 57,93%.
Итак, примерно 59,87% растений в этом саду имеют высоту более 26 дюймов.
Пример 3
Вес определенного вида дельфинов обычно распределяется со средним значением μ = 400 фунтов и стандартным отклонением σ = 25 фунтов. Приблизительно какой процент дельфинов весит от 410 до 425 фунтов?
Шаг 1: Найдите z-показатели.
Сначала мы найдем z-показатели, связанные с 410 книгами и 425 книгами.
z-показатель 410 = (x – μ) / σ = (410 – 400) / 25 = 10/25 = 0,4
z-оценка 425 = (x – µ) / σ = (425 – 400) / 25 = 25 / 25 = 1
Шаг 2. Используйте диаграмму z, чтобы найти проценты, соответствующие каждому показателю z.
Сначала мы найдем значение 0,4. в таблице з:

Далее мы будем искать значение 1 в таблице з:

Наконец, мы вычтем наименьшее значение из наибольшего значения: 0,8413 – 0,6554 = 0,1859 .
Так, примерно 18,59% дельфинов весят от 410 до 425 фунтов.
Дополнительные ресурсы
Введение в нормальное распределение
Калькулятор площади нормального распределения
Калькулятор Z-оценки