Как найти значение p по показателю z в excel
Многие проверки гипотез в статистике приводят к получению статистики z-теста. Как только мы находим эту статистику z-теста, мы обычно находим связанное с ней значение p. Если это значение p ниже определенного альфа-уровня (например, 0,10, 0,05, 0,01), то мы отвергаем нулевую гипотезу теста и делаем вывод, что наши результаты значимы.
В этом руководстве показано несколько примеров поиска значения p по z-показателю в Excel с помощью функции НОРМ.РАСП , которая принимает следующие аргументы:
НОРМ.РАСП (x, среднее, стандартное_отклонение, совокупное)
Золото:
- x — это показатель z, который нас интересует.
- среднее значение — это среднее значение распределения. Мы будем использовать «0» для стандартного нормального распределения.
- Standard_dev — это стандартное отклонение распределения. Мы будем использовать «1» для стандартного нормального распределения.
- кумулятивная функция принимает значение «ИСТИНА» (возвращает CDF) или «ЛОЖЬ» (возвращает PDF) – мы будем использовать «ИСТИНА», чтобы получить значение кумулятивной функции распределения.
Давайте посмотрим несколько примеров.
Пример 1. Определение значения P по показателю Z (двусторонний критерий)
Компания хочет знать, отличается ли средний срок службы батареи нового типа от текущей стандартной батареи, средний срок службы которой составляет 18 часов. В случайной выборке из 100 новых батарей они обнаружили, что средний срок службы составляет 19 часов со стандартным отклонением 4 часа.
Выполните двусторонний тест гипотезы, используя альфа-уровень 0,05, чтобы определить, отличается ли средний срок службы новой батареи от среднего срока службы текущей стандартной батареи.
Шаг 1: Сформулируйте гипотезы.
Нулевая гипотеза (H 0 ): µ = 18
Альтернативная гипотеза: (Ха): μ ≠ 18.
Шаг 2: Найдите статистику z-теста.
Статистика теста z = (x-μ) / (s/√n) = (19-18) / (4/√100) = 2,5
Шаг 3: Найдите p-значение статистики z-теста с помощью Excel.
Чтобы найти значение p для z = 2,5, мы будем использовать следующую формулу в Excel: =1 – НОРМ.РАСП(2,5, 0, 1, ИСТИНА)
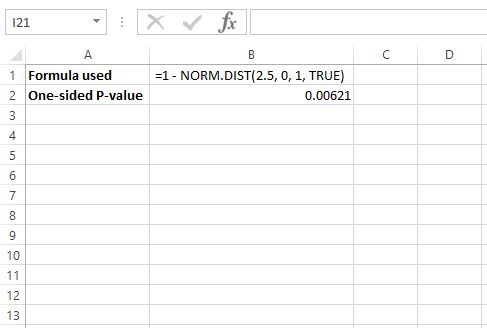
Это говорит нам о том, что одностороннее значение p равно 0,00621 , но поскольку мы выполняем двусторонний тест, нам нужно умножить это значение на 2, поэтому значение p будет 0,00612 * 2 = 0,01224 .
Шаг 4: Отклонить или не отвергать нулевую гипотезу.
Поскольку значение p 0,01224 меньше выбранного альфа-уровня 0,05 , мы отвергаем нулевую гипотезу. У нас достаточно доказательств, чтобы сказать, что средний срок службы новой батареи значительно отличается от среднего срока службы нынешней стандартной батареи.
Пример 2: Определение значения P по показателю Z (односторонний тест)
Ботаник подсчитал, что средняя высота определенного растения составляет менее 14 дюймов. Она случайным образом выбирает 30 растений и измеряет их. Она обнаружила, что средний рост составляет 13,5 дюймов со стандартным отклонением в 2 дюйма.
Выполните односторонний тест гипотезы, используя альфа-уровень 0,01, чтобы определить, действительно ли средняя высота этого растения меньше 14 дюймов.
Шаг 1: Сформулируйте гипотезы.
Нулевая гипотеза (H0): μ≥ 14
Альтернативная гипотеза: (Ha): μ < 14
Шаг 2: Найдите статистику z-теста.
Статистика теста z = (x-μ) / (s/√n) = (13,5-14) / (2/√30) = -1,369
Шаг 3: Найдите p-значение статистики z-теста с помощью Excel.
Чтобы найти значение p для z = -1,369, мы будем использовать следующую формулу в Excel: =НОРМ.РАСП(-1,369, 0, 1, ИСТИНА)
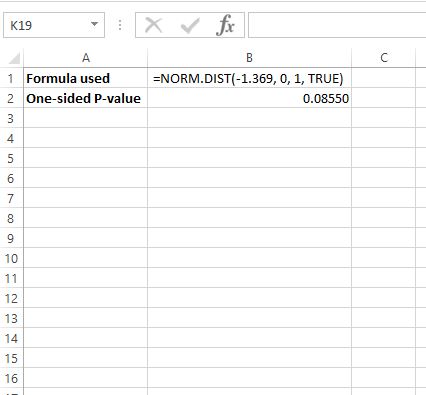
Это говорит нам о том, что одностороннее значение p равно 0,08550 .
Шаг 4: Отклонить или не отвергать нулевую гипотезу.
Поскольку значение p 0,08550 больше выбранного альфа-уровня 0,01 , мы не можем отвергнуть нулевую гипотезу. У нас нет достаточных доказательств, чтобы сказать, что средняя высота этого вида растений составляет менее 14 дюймов.
Дополнительные руководства по статистике в Excel можно найти в нашем полном списке руководств по Excel .