Как рассчитать vif в excel
Мультиколлинеарность в регрессионном анализе возникает, когда две или более объясняющих переменных сильно коррелируют друг с другом, так что они не предоставляют уникальную или независимую информацию в регрессионной модели. Если степень корреляции между переменными достаточно высока, это может вызвать проблемы при подборе и интерпретации регрессионной модели.
К счастью, можно обнаружить мультиколлинеарность с помощью показателя, называемого коэффициентом инфляции дисперсии (VIF) , который измеряет корреляцию и силу корреляции между объясняющими переменными в регрессионной модели.
В этом уроке объясняется, как рассчитать VIF в Excel.
Пример: расчет VIF в Excel
В этом примере мы выполним множественную линейную регрессию, используя следующий набор данных, описывающий характеристики 10 баскетболистов. Мы подберем регрессионную модель, используя рейтинг в качестве переменной ответа и очки, передачи и подборы в качестве объясняющих переменных. Далее мы определим значения VIF для каждой объясняющей переменной.
Шаг 1. Выполните множественную линейную регрессию.
На верхней ленте перейдите на вкладку «Данные» и нажмите «Анализ данных». Если вы не видите эту опцию, вам необходимо сначала установить бесплатное программное обеспечение Analysis ToolPak .

После того, как вы нажмете «Анализ данных», появится новое окно. Выберите «Регрессия» и нажмите «ОК».

Заполните необходимые таблицы для переменных ответа и независимых переменных, затем нажмите «ОК».
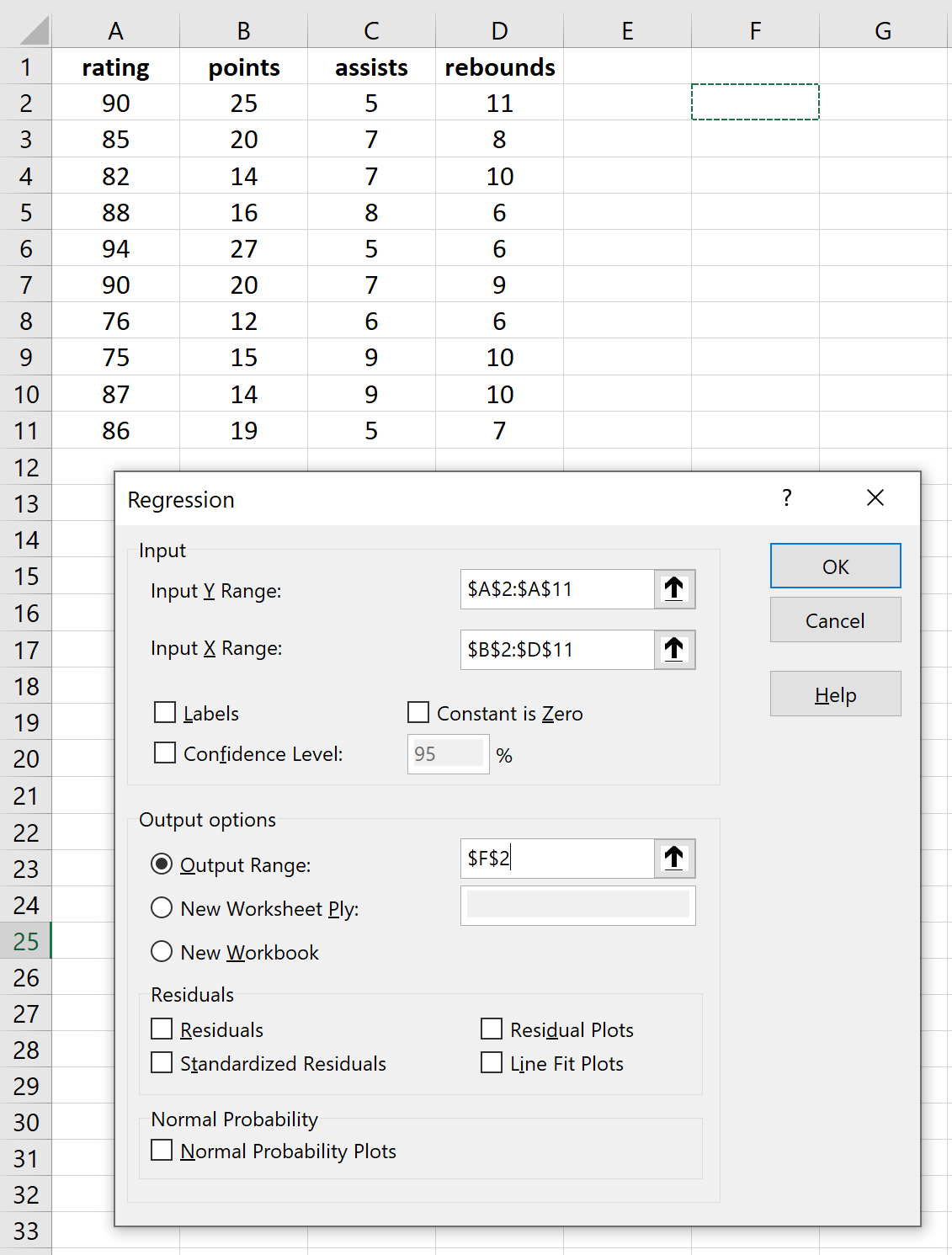
Это дает следующий результат:
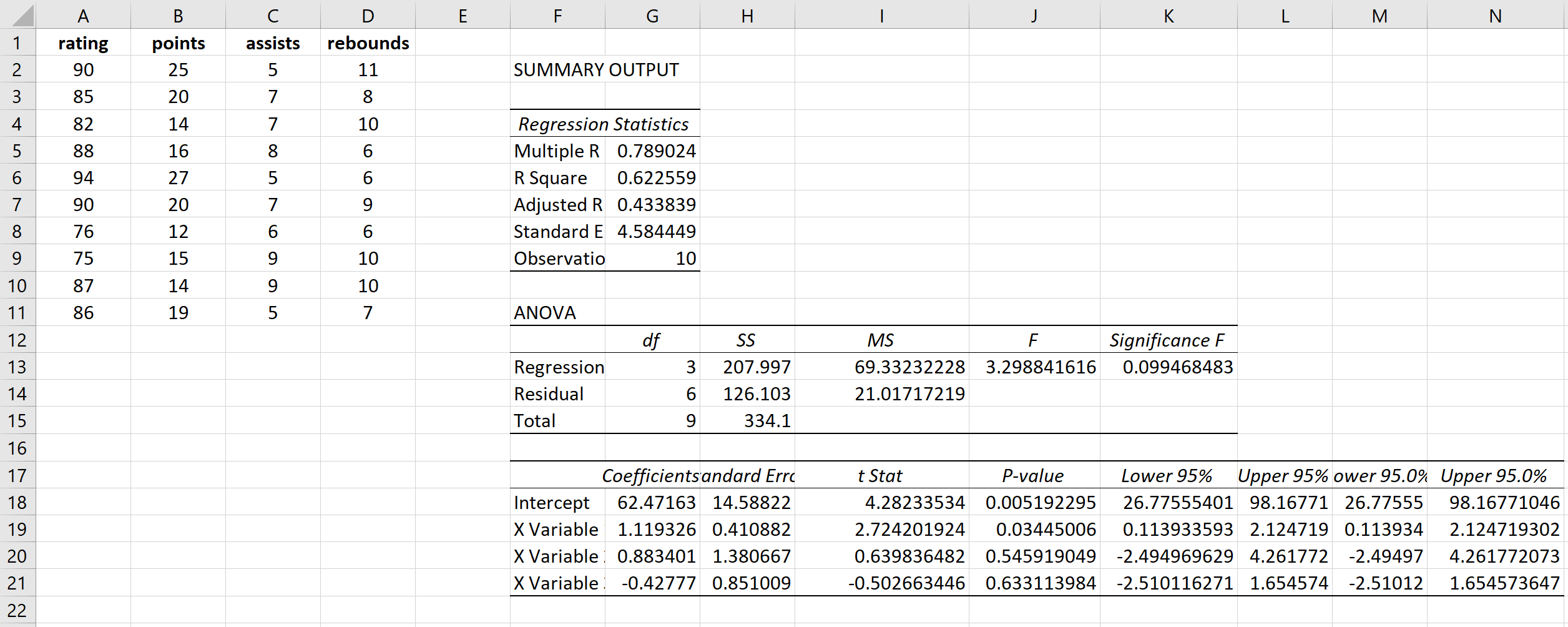
Шаг 2: Рассчитайте VIF для каждой объясняющей переменной.
Затем мы можем рассчитать VIF для каждой из трех объясняющих переменных, выполнив отдельные регрессии, используя одну объясняющую переменную в качестве переменной отклика, а две другие — в качестве объясняющих переменных.
Например, мы можем рассчитать VIF для переменной очков , выполнив множественную линейную регрессию, используя очки в качестве переменной ответа, а передачи и подборы в качестве объясняющих переменных.
Это дает следующий результат:

VIF для очков рассчитывается как 1/(1 – R Square) = 1/(1 – 0,433099) = 1,76 .
Затем мы можем повторить этот процесс для двух других переменных: передач и подборов .
Оказывается, что VIF для трех объясняющих переменных выглядят следующим образом:
баллы: 1,76
передачи: 1,96
подборы: 1,18
Как интерпретировать значения VIF
Значение VIF начинается с 1 и не имеет верхнего предела. Общее правило интерпретации VIF следующее:
- Значение 1 указывает на отсутствие корреляции между данной объясняющей переменной и любой другой объясняющей переменной в модели.
- Значение от 1 до 5 указывает на умеренную корреляцию между данной объясняющей переменной и другими объясняющими переменными в модели, но часто она недостаточно серьезна, чтобы требовать особого внимания.
- Значение больше 5 указывает на потенциально серьезную корреляцию между данной объясняющей переменной и другими объясняющими переменными в модели. В этом случае оценки коэффициентов и значения p в результатах регрессии, скорее всего, ненадежны.
Поскольку каждое из значений VIF объясняющих переменных в нашей регрессионной модели близко к 1, мультиколлинеарность не является проблемой в нашем примере.