Как посчитать sxy в статистике (с примером)
В статистике Sxy представляет собой сумму произведения разностей между значениями x и средним значением x и разностей между значениями y и средним значением y.
Это значение часто рассчитывается при ручной настройке простой модели линейной регрессии .
Для расчета Sxy мы используем следующую формулу:
Sxy = Σ(x i – x ) (y i – y )
Золото:
- Σ : Символ, означающий «сумма».
- x i : i- е значение x
- x : Среднее значение x
- y i : i-е значение y
- y : Среднее значение y
Следующий пример показывает, как использовать эту формулу на практике.
Пример: расчет Sxy вручную
Предположим, мы хотим подогнать простую модель линейной регрессии к следующему набору данных:
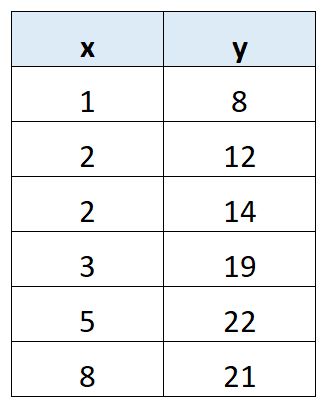
Предположим, мы хотим вычислить Sxy для этого набора данных.
Прежде всего, мы должны вычислить среднее значение x:
- х = (1 + 2 + 2 + 3 + 5 + 8) / 6 = 3,5
Затем мы должны вычислить среднее значение y:
- у = (8 + 12 + 14 + 19 + 22 + 21) / 6 = 16
Используя эти значения, на следующем снимке экрана показано, как вычислить значение Sxy:
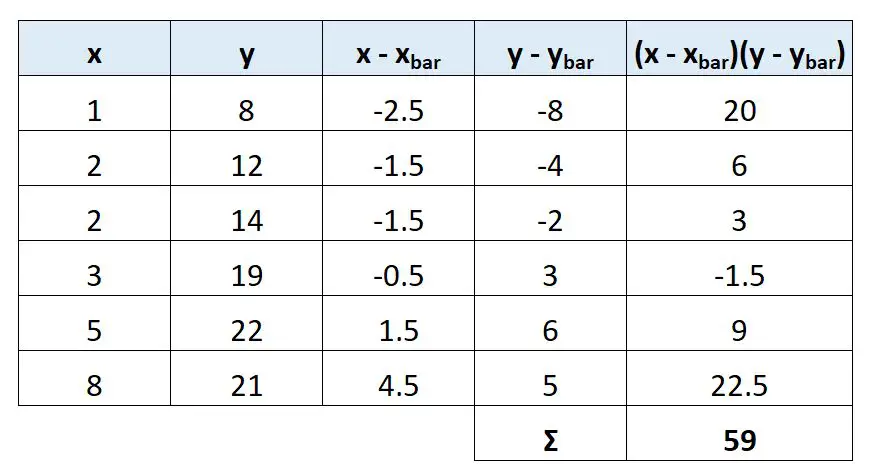
Значение Sxy оказывается равным 59 .
Обратите внимание, что мы также можем использовать калькулятор Sxy для автоматического расчета значения Sxy для этой модели:

Калькулятор возвращает значение 59 , которое мы вычислили вручную.
Обратите внимание, что мы используем следующие формулы для ручного выполнения простой линейной регрессии:
у = а + Ьх
Золото:
- а = у – bx
- б = Sxy / Sxx
Расчет Sxy — это всего лишь расчет, который нам нужно выполнить, чтобы соответствовать простой модели линейной регрессии.
Связанный: Как рассчитать Sxx в статистике
Дополнительные ресурсы
В следующих руководствах объясняется, как выполнять другие распространенные задачи в статистике:
Как выполнить простую линейную регрессию вручную
Как выполнить множественную линейную регрессию вручную