Как читать ковариационную матрицу
Ковариация — это мера того, как изменения одной переменной связаны с изменениями второй переменной. Более конкретно, это мера степени линейной связи двух переменных.
Ковариационная матрица — это квадратная матрица, показывающая ковариацию между множеством различных переменных. Это может быть полезным способом понять, как различные переменные связаны в наборе данных.
В следующем примере показано, как читать ковариационную матрицу на практике.
Как читать ковариационную матрицу
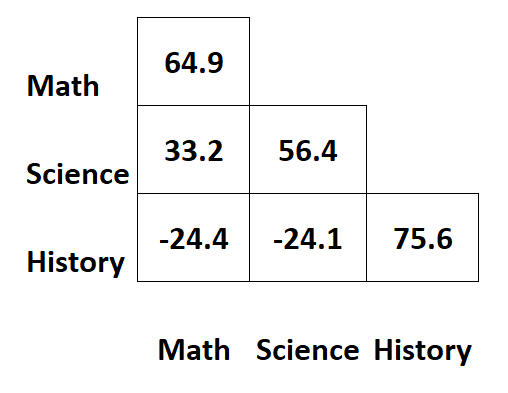
Предположим, у нас есть следующая ковариационная матрица, содержащая информацию об экзаменационных баллах учащихся по трем различным предметам:
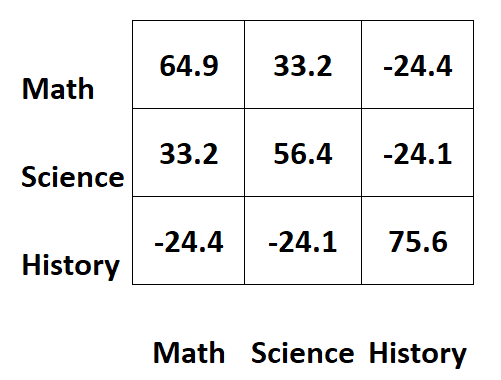
Значения по диагоналям матрицы представляют собой дисперсии каждого предмета. 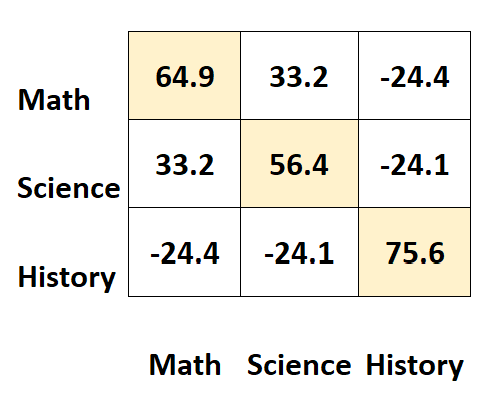
Например:
- Дисперсия результатов математических вычислений составляет 64,9 .
- Дисперсия оценок по естествознанию составляет 56,4 .
- Дисперсия исторических оценок составляет 75,6 .
Остальные значения матрицы представляют собой ковариации между разными субъектами.
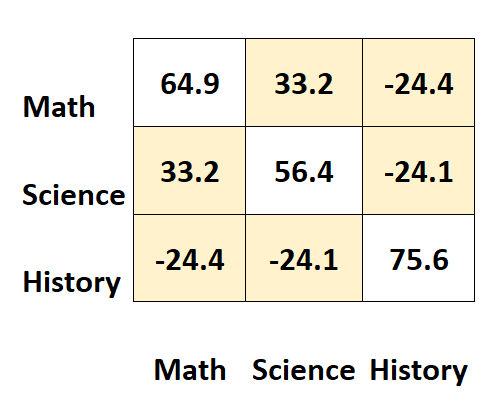
Например:
- Ковариация между оценками по математике и естественным наукам составляет 33,2 .
- Ковариация между оценками по математике и истории составляет –24,4 .
- Ковариация между оценками по естествознанию и истории составляет –24,1 .
Положительное число ковариации указывает на то, что две переменные имеют тенденцию увеличиваться или уменьшаться одновременно.
Например, математика и естественные науки имеют положительную ковариацию ( 33,2 ), что указывает на то, что учащиеся, набравшие высокие баллы по математике, также имеют тенденцию получать высокие баллы по естественным наукам.
И наоборот, учащиеся, которые плохо успевают по математике, также, как правило, плохо успевают по естественным наукам.
Отрицательное число ковариации указывает на то, что по мере увеличения одной переменной вторая переменная имеет тенденцию к уменьшению.
Например, математика и история имеют отрицательную ковариацию ( -24,44 ), что указывает на то, что учащиеся с высокими показателями по математике, как правило, имеют низкие результаты по истории.
И наоборот, учащиеся с низкими баллами по математике, как правило, получают высокие баллы по истории.
Замечание о симметрии ковариационной матрицы
Следует отметить, что ковариационная матрица совершенно симметрична.
Например, в верхней правой ячейке отображается точно то же значение, что и в нижней левой ячейке:
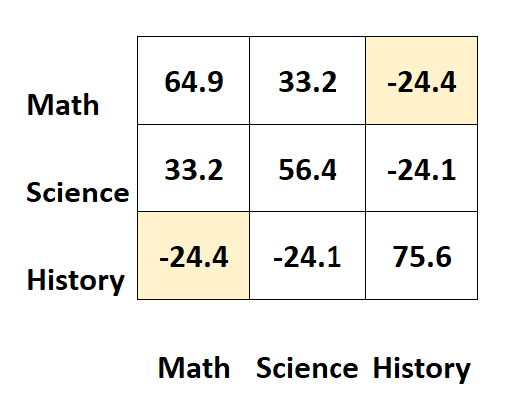
Действительно, эти две ячейки измеряют ковариацию между историей и математикой.
Поскольку ковариационная матрица симметрична, половина значений ковариации, отображаемых в матрице, являются избыточными и ненужными.
Итак, иногда отображается только половина ковариационной матрицы:
Когда использовать ковариационную матрицу
На практике вам часто придется создавать и интерпретировать матрицу корреляции чаще, чем ковариационную матрицу.
Однако ковариационные матрицы часто используются «под капотом» для различных алгоритмов и моделей машинного обучения.
Например, ковариационная матрица используется при анализе главных компонентов , что помогает нам понять основные закономерности в наборе данных, содержащем большое количество переменных.
Дополнительные ресурсы
В следующих руководствах объясняется, как создать ковариационную матрицу с использованием различного статистического программного обеспечения:
Как создать ковариационную матрицу в R
Как создать ковариационную матрицу в Python
Как создать ковариационную матрицу в SPSS
Как создать ковариационную матрицу в Excel