Как читать корреляционную матрицу
В статистике мы часто стремимся понять взаимосвязь между двумя переменными.
Например, мы можем захотеть понять взаимосвязь между количеством часов обучения студента и оценкой, которую он получает на экзамене.
Один из способов количественной оценки этой взаимосвязи – использовать коэффициент корреляции Пирсона , который является мерой линейной связи между двумя переменными . Он имеет значение от -1 до 1, где:
- -1 указывает на совершенно отрицательную линейную корреляцию между двумя переменными.
- 0 указывает на отсутствие линейной корреляции между двумя переменными.
- 1 указывает на совершенно положительную линейную корреляцию между двумя переменными.
Чем дальше коэффициент корреляции от нуля, тем сильнее связь между двумя переменными.
Связанный: Что считается «сильной» корреляцией?
Но в некоторых случаях мы хотим понять корреляцию между несколькими парами переменных. В этих случаях мы можем создать матрицу корреляции , которая представляет собой квадратную таблицу, показывающую коэффициенты корреляции между несколькими переменными.
Пример корреляционной матрицы
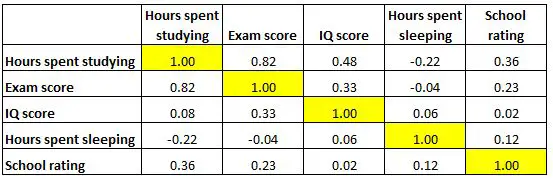
В приведенной ниже матрице корреляции представлены коэффициенты корреляции между несколькими переменными, связанными с образованием:
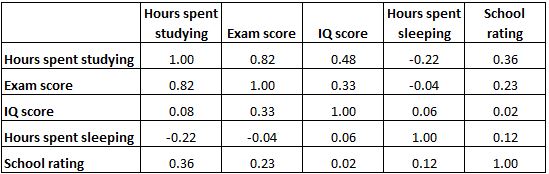
Каждая ячейка таблицы показывает корреляцию между двумя конкретными переменными. Например, выделенная ячейка ниже показывает, что корреляция между «часами, потраченными на учебу» и «оценкой на экзамене» составляет 0,82 , что указывает на их сильную положительную корреляцию. Больше часов, потраченных на учебу, тесно связано с более высокими баллами на экзаменах.
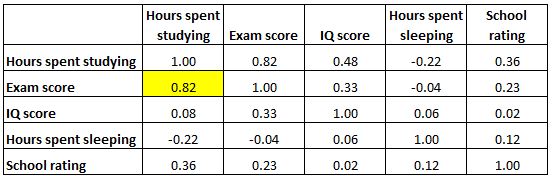
А выделенная ячейка ниже показывает, что корреляция между «часами, потраченными на учебу» и «часами, потраченными на сон» составляет -0,22 , что указывает на слабую отрицательную корреляцию. Больше часов, потраченных на учебу, связано с меньшим количеством часов, проведенных на сне.
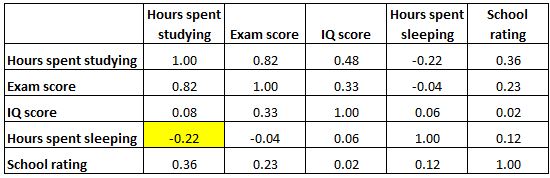
А выделенная ячейка ниже показывает, что корреляция между «часами, проведенными во сне» и «оценкой IQ» составляет 0,06 , что указывает на то, что они практически не коррелируют. Существует очень слабая связь между количеством часов, в течение которых студент спит, и его показателем IQ.
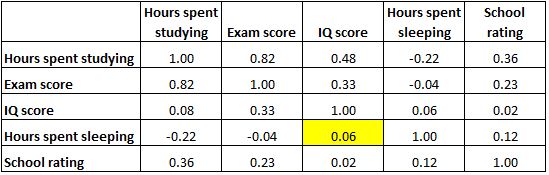
Также обратите внимание, что все коэффициенты корреляции по диагонали таблицы равны 1, поскольку каждая переменная идеально коррелирует сама с собой. Эти ячейки бесполезны для интерпретации.
Вариации корреляционной матрицы
Обратите внимание, что корреляционная матрица совершенно симметрична. Например, в верхней правой ячейке отображается точно то же значение, что и в нижней левой ячейке:
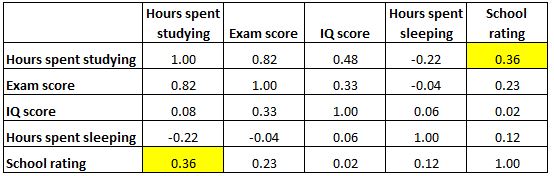
Действительно, эти две ячейки измеряют корреляцию между «часами, потраченными на учебу» и «школьной оценкой».
Поскольку матрица корреляции симметрична, половина коэффициентов корреляции, отображаемых в матрице, являются избыточными и ненужными. Так, иногда будет отображаться только половина корреляционной матрицы:
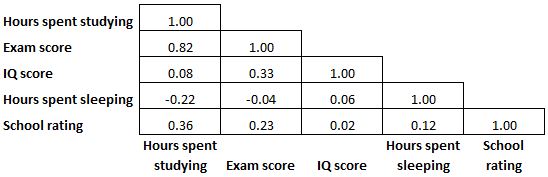
А иногда матрицу корреляции раскрашивают как тепловую карту, чтобы коэффициенты корреляции было еще легче читать:

Когда использовать корреляционную матрицу
На практике корреляционная матрица обычно используется по трем причинам:
1. Корреляционная матрица удобно суммирует набор данных.
Матрица корреляции — это простой способ суммировать корреляции между всеми переменными в наборе данных. Например, предположим, что у нас есть следующий набор данных, содержащий следующую информацию для 1000 студентов:
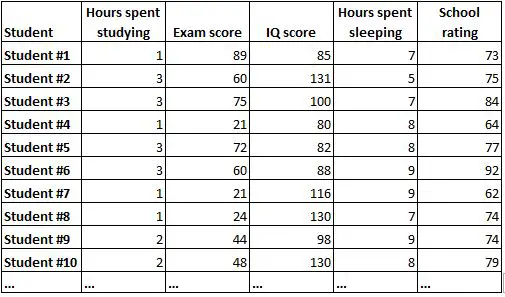
Было бы очень сложно понять взаимосвязь между каждой переменной, просто взглянув на необработанные данные. К счастью, корреляционная матрица может помочь нам быстро понять корреляции между каждой парой переменных.
2. Корреляционная матрица служит диагностикой регрессии.
Одним из ключевых предположений множественной линейной регрессии является то, что ни одна независимая переменная в модели не имеет сильной корреляции с какой-либо другой переменной в модели.
Когда две независимые переменные сильно коррелируют, это приводит к проблеме, называемой мультиколлинеарностью , и может затруднить интерпретацию результатов регрессии.
Один из самых простых способов обнаружить потенциальную проблему мультиколлинеарности — посмотреть на матрицу корреляции и визуально проверить, сильно ли коррелируют какие-либо переменные друг с другом.
3. Корреляционная матрица может использоваться в качестве входных данных для других анализов.
Корреляционная матрица используется в качестве входных данных для других сложных анализов, таких как исследовательский факторный анализ и модели структурных уравнений.
Дополнительные ресурсы
В следующих руководствах объясняется, как создать корреляционную матрицу с помощью различного статистического программного обеспечения:
Как создать матрицу корреляции в Excel
Как создать матрицу корреляции в SPSS
Как создать корреляционную матрицу в Stata
Как создать матрицу корреляции в Python