Как посчитать коэффициент корреляции на калькуляторе ти-84
Коэффициент корреляции — это мера линейной связи между двумя переменными. Он может принимать значение от -1 до 1, где:
- -1 указывает на совершенно отрицательную линейную корреляцию между двумя переменными.
- 0 указывает на отсутствие линейной корреляции между двумя переменными.
- 1 указывает на совершенно положительную линейную корреляцию между двумя переменными.
Вы можете использовать следующие шаги для расчета коэффициента корреляции между двумя переменными на калькуляторе TI-84:
Шаг 1. Включите диагностику.
Для начала нам нужно включить диагностику. Для этого нажмите 2, затем нажмите цифру 0. Это приведет нас к экрану КАТАЛОГ.
Прокрутите до пункта «Диагностика включена» и нажмите ENTER .
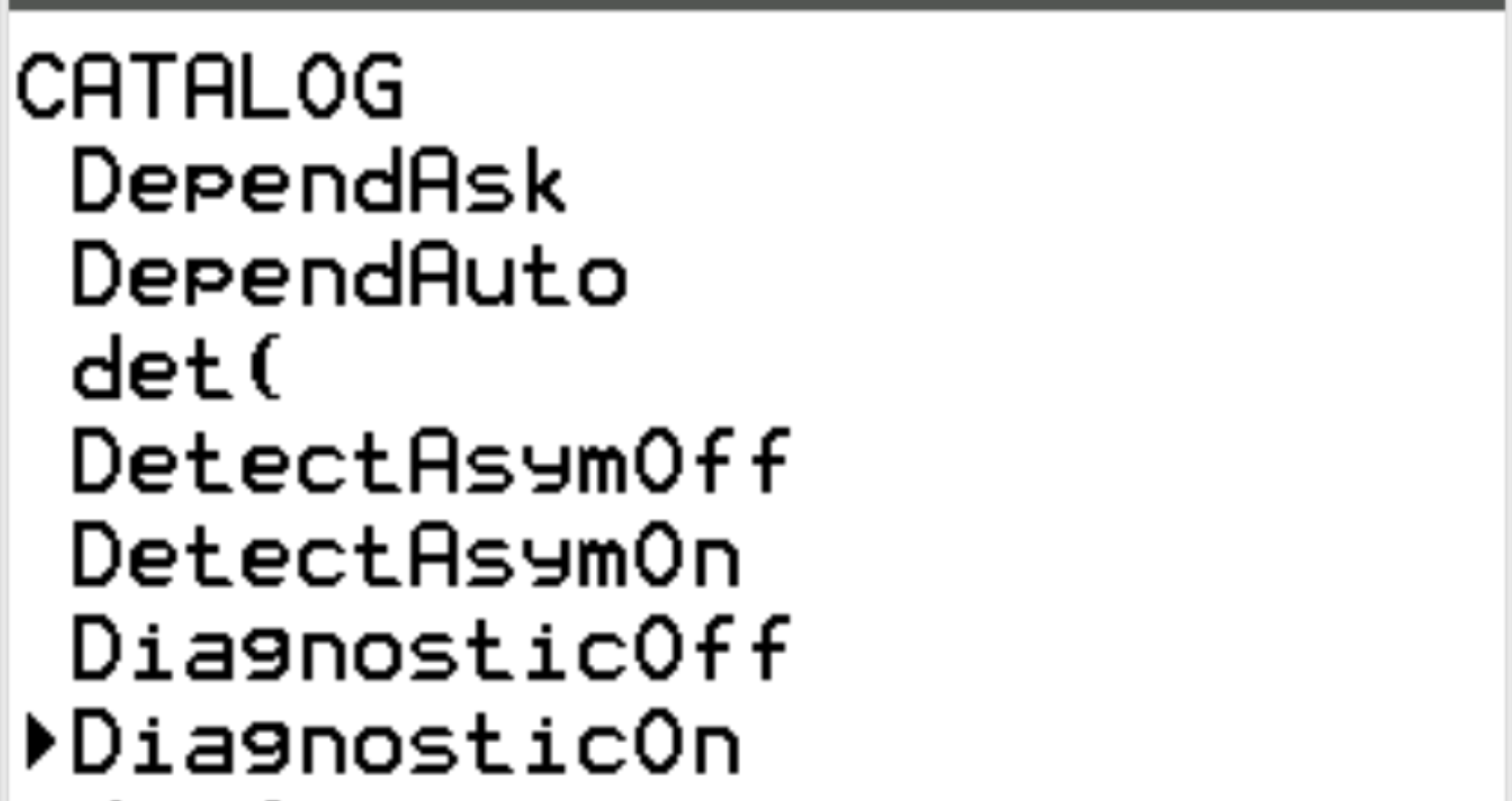
Затем снова нажмите ENTER .
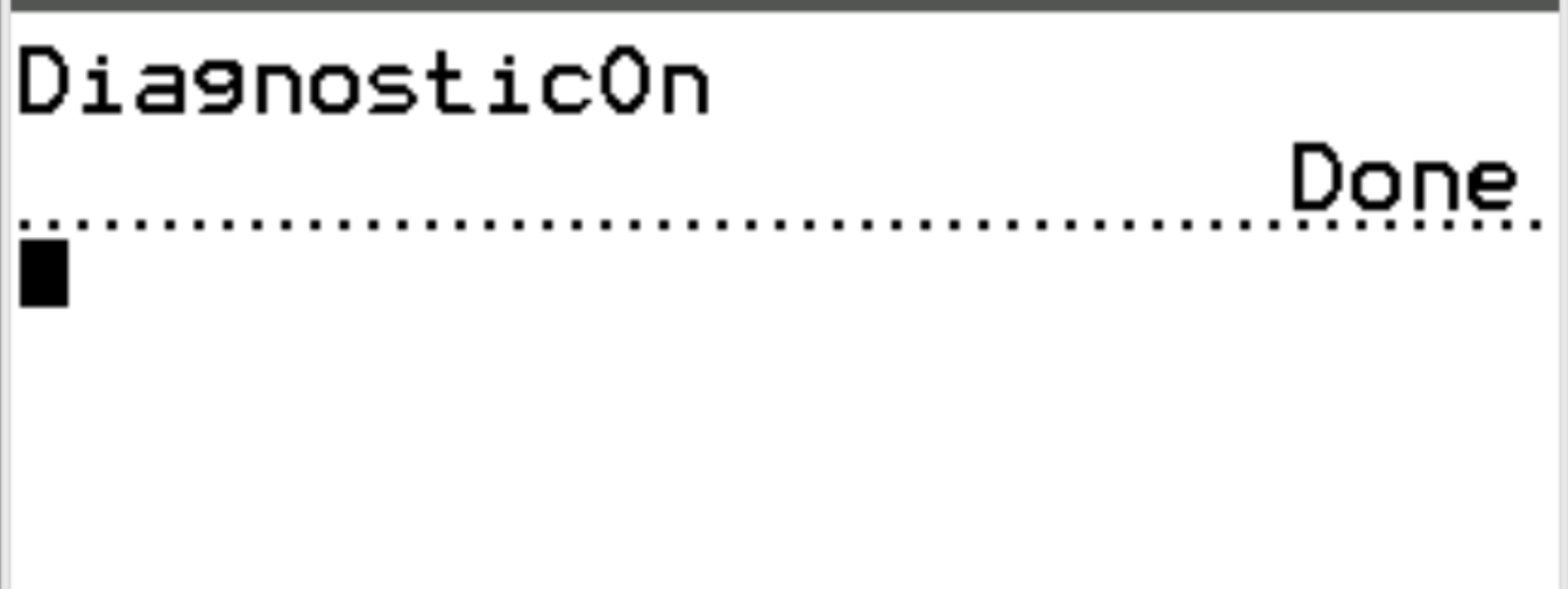
Диагностика теперь включена, поэтому мы можем рассчитать коэффициент корреляции между двумя переменными.
Шаг 2: Введите данные.
Далее нам нужно ввести значения данных для наших двух переменных. Нажмите Stat , затем нажмите EDIT . Введите значения первой переменной в столбец L1 и значения второй переменной в столбец L2:
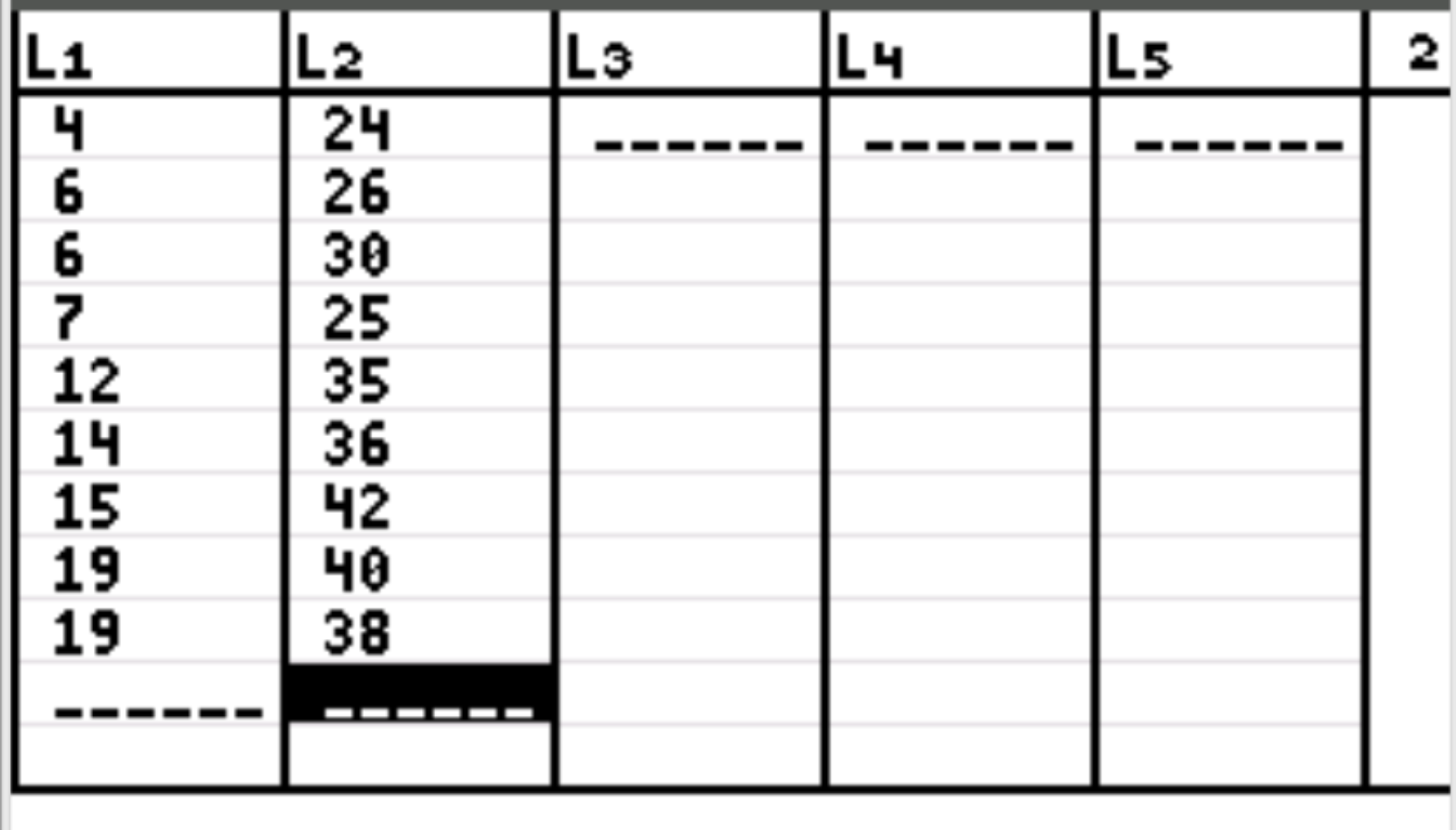
Шаг 3: Найдите коэффициент корреляции.
Далее мы рассчитаем коэффициент корреляции между двумя переменными. Нажмите Stat , затем перейдите к CALC . Затем прокрутите до 8: Linreg(a+bx) и нажмите Enter .
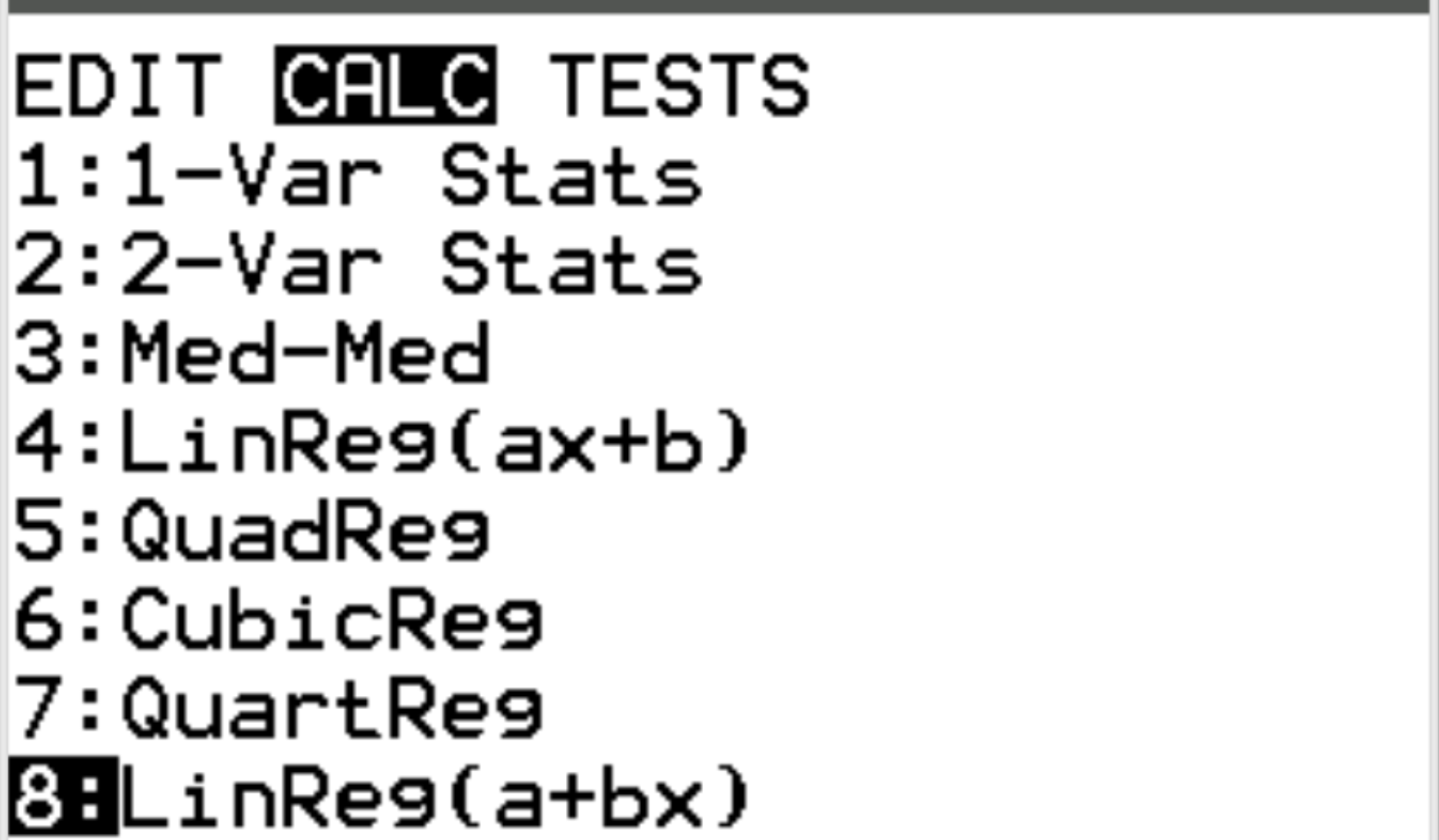
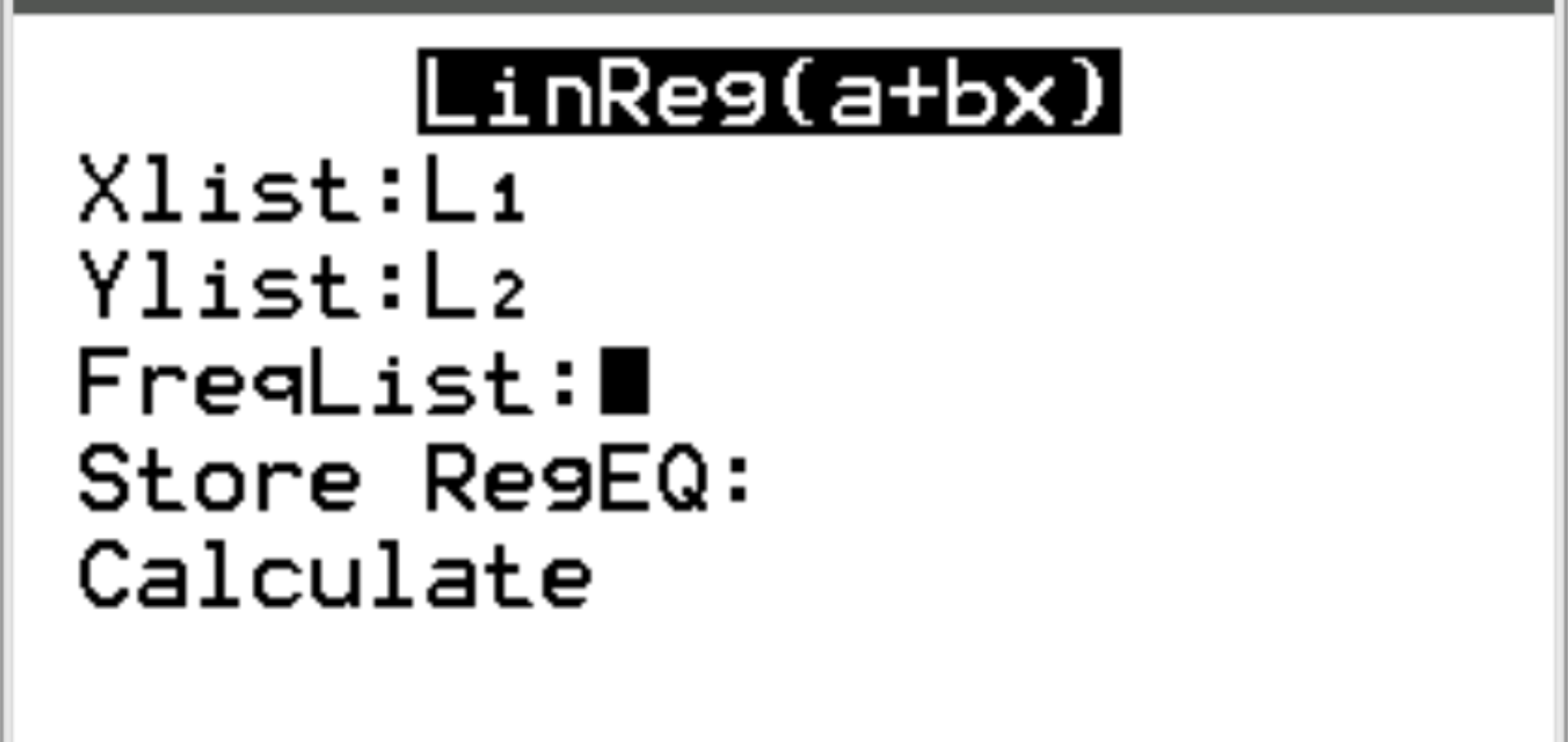
Для Xlist и Ylist убедитесь, что выбраны L1 и L2, поскольку это столбцы, которые мы использовали для ввода наших данных. Оставьте FreqList пустым. Прокрутите вниз до пункта «Рассчитать» и нажмите Enter .
На новом экране мы видим, что коэффициент корреляции (r) между двумя переменными равен 0,9145 .
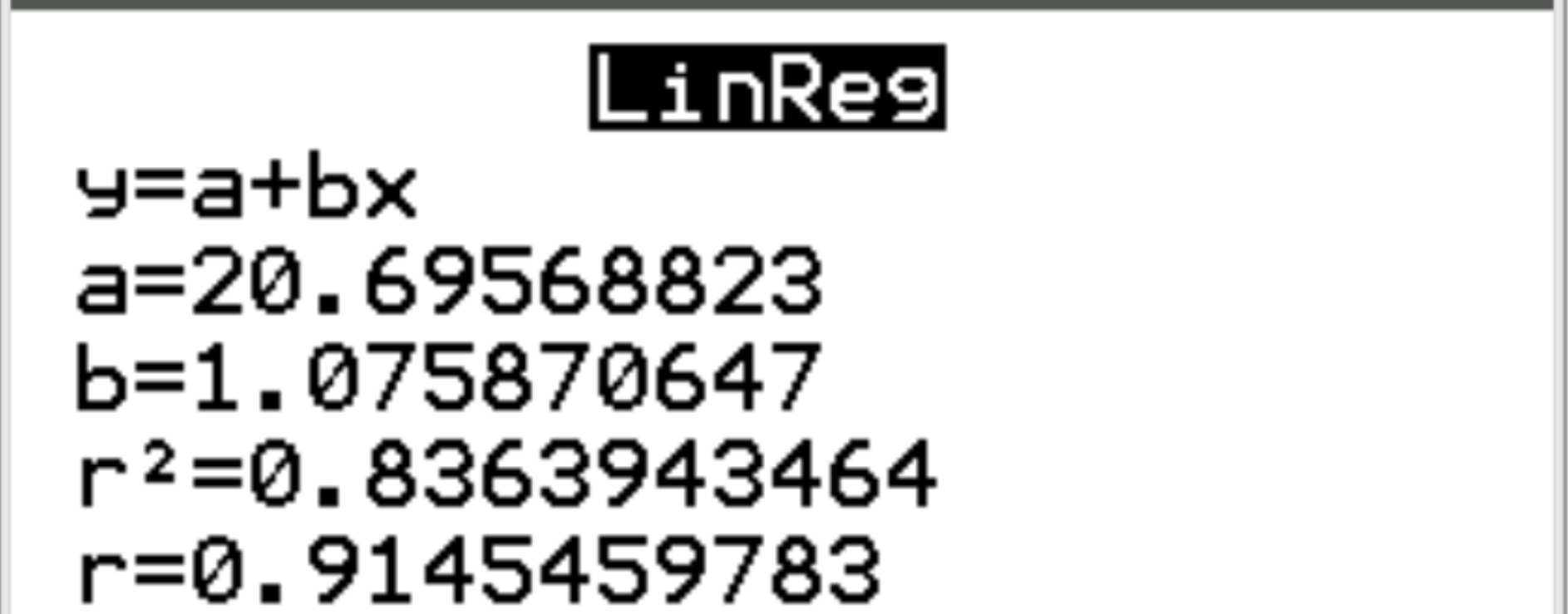
Как интерпретировать коэффициент корреляции
В следующей таблице показано практическое правило интерпретации силы связи между двумя переменными на основе значения r :
| Абсолютное значение r | Сила отношений |
|---|---|
| р < 0,25 | Нет отношений |
| 0,25 < г < 0,5 | Слабые отношения |
| 0,5 < г < 0,75 | Умеренные отношения |
| г > 0,75 | Прочные отношения |
В нашем примере коэффициент корреляции 0,9145 указывает на сильную положительную связь между двумя переменными.
Об авторе
бенджамин андерсон
Здравствуйте, я Бенджамин, профессор статистики на пенсии, ставший преданным преподавателем Statorials. Имея обширный опыт и знания в области статистики, я хочу поделиться своими знаниями, чтобы расширить возможности студентов с помощью Statorials. Узнать больше