Как рассчитать нормальные вероятности на калькуляторе ti-84
Нормальное распределение является наиболее часто используемым распределением во всей статистике. В этом руководстве объясняется, как использовать следующие функции калькулятора TI-84 для нахождения вероятностей нормального распределения:
Normalpdf(x, μ, σ) возвращает вероятность, связанную с нормальным PDF-файлом, где:
- x = индивидуальное значение
- μ = среднее значение численности населения
- σ = стандартное отклонение генеральной совокупности
normalcdf(lower_x, Upper_x, μ, σ) возвращает кумулятивную вероятность, связанную с нормальным CDF между двумя значениями.
Золото:
- low_x = нижнее индивидуальное значение
- Upper_x = верхнее индивидуальное значение
- μ = среднее значение численности населения
- σ = стандартное отклонение генеральной совокупности
Эти две функции доступны на калькуляторе TI-84, нажав 2nd, а затем нажав vars . Это приведет вас к экрану DISTR , где вы сможете использоватьnormalpdf () иnormalcdf () :
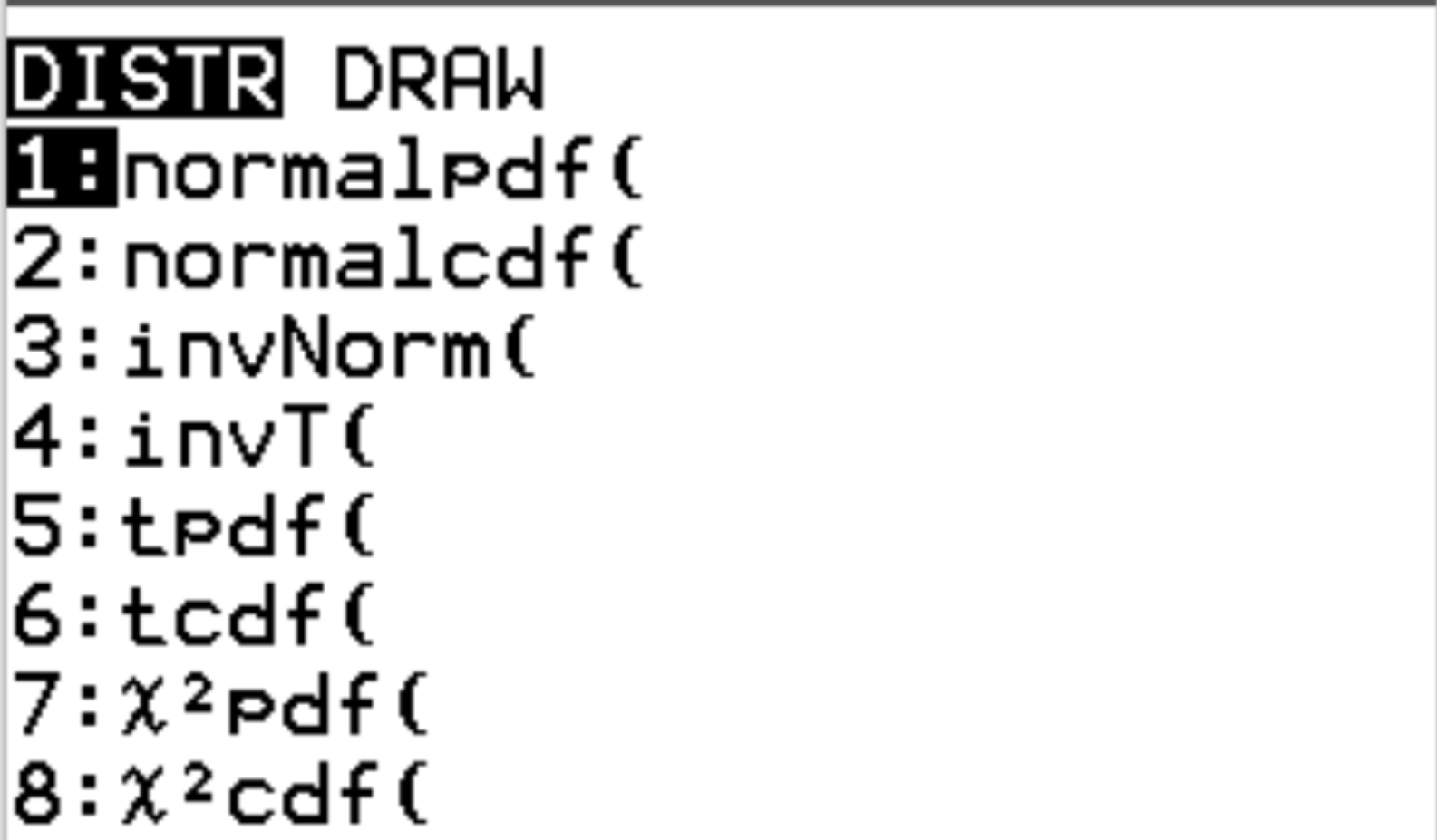
Следующие примеры иллюстрируют, как использовать эти функции для ответа на различные вопросы.
Пример 1: нормальная вероятность больше x
Вопрос: Для нормального распределения со средним значением = 40 и стандартным отклонением = 6 найдите вероятность того, что значение превышает 45.
Ответ: Используйте функциюnormalcdf(x, 10000, μ, σ):
нормальныйcdf(45, 10000, 40, 6) = 0,2023
Примечание. Поскольку для функции требуется значение Upper_x, мы просто используем 10 000.
Пример 2: нормальная вероятность меньше x
Вопрос: Для нормального распределения со средним значением = 100 и стандартным отклонением = 11,3 найдите вероятность того, что значение меньше 98.
Ответ: Используйте функциюnormalcdf(-10000, x, μ, σ):
нормальныйcdf(-10000, 98, 100, 11,3) = 0,4298
Примечание. Поскольку для функции требуется значение low_x, мы просто используем -10000.
Пример 3: Нормальная вероятность между двумя значениями
Вопрос: Для нормального распределения со средним значением = 50 и стандартным отклонением = 4 найдите вероятность того, что значение находится между 48 и 52.
Ответ: используйте функциюnormalcdf(smaller_x, Larger_x, μ, σ).
нормальныйcdf(48, 52, 50, 4) = 0,3829
Пример 4: Нормальная вероятность, кроме двух значений
Вопрос: Для нормального распределения со средним значением = 22 и стандартным отклонением = 4 найдите вероятность того, что значение меньше 20 или больше 24.
Ответ: Используйте функциюnormalcdf(-10000, small_x, μ, σ) +normalcdf(larger_x, 10000, μ, σ)
нормальныйcdf(-10000, 20, 22, 4) + нормальныйcdf(24, 10000, 22, 4) = 0,6171