Что такое категориальное распределение?
Категориальное распределение — это дискретное распределение вероятностей, которое описывает вероятность того, что случайная величина примет значение, принадлежащее одной из K категорий, где каждая категория связана с вероятностью.
Чтобы распределение можно было классифицировать как категориальное распределение, оно должно соответствовать следующим критериям:
- Категории дискретны.
- Есть две или более потенциальных категорий.
- Вероятность того, что случайная величина примет значение в каждой категории, должна находиться в диапазоне от 0 до 1.
- Сумма вероятностей для всех категорий должна составлять 1.
Наиболее очевидным примером категориального распределения является распределение результатов, связанных с броском игральной кости. Существует K = 6 потенциальных исходов, и вероятность каждого исхода равна 1/6:
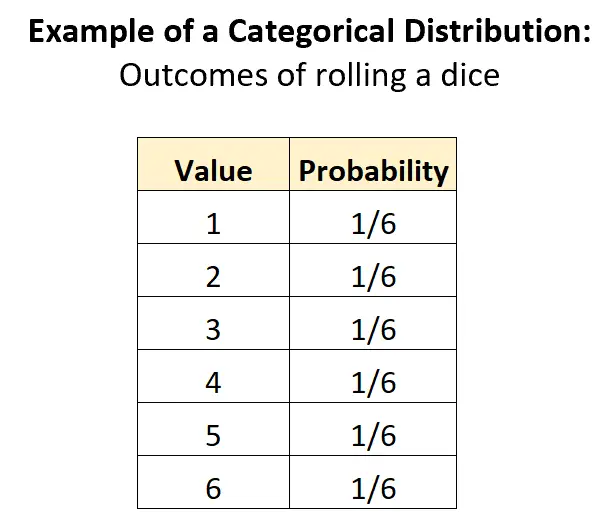
Это распределение соответствует всем критериям, позволяющим отнести его к категориальному распределению:
- Категории дискретны (например, случайная величина может принимать только дискретные значения – 1, 2, 3, 4, 5, 6)
- Есть две или более потенциальных категорий.
- Вероятность каждой категории находится между 0 и 1.
- Сумма вероятностей составляет 1: 1/6 + 1/6 + 1/6 + 1/6 + 1/6 + 1/6 = 1.
Главное правило:
Если вы можете подсчитать количество исходов, то вы работаете с дискретной случайной величиной — например, подсчитываете, сколько раз монета выпала орлом.
Но если вы можете измерить результат, вы работаете с непрерывной случайной величиной — например, измеряете рост, вес, время и т. д.
Другие примеры категориальных распределений
В реальном мире существует множество категориальных распределений, в том числе:
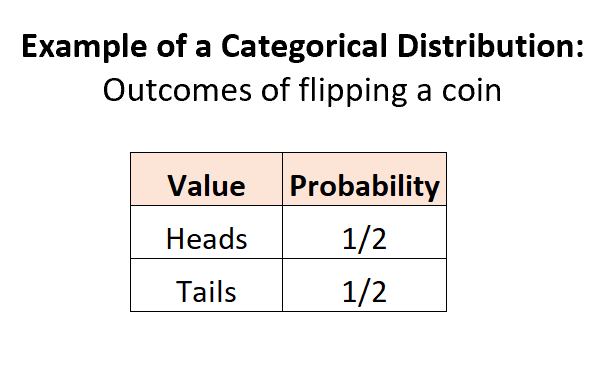
Пример 1: Подбросьте монету.
Когда мы подбрасываем монету, есть два потенциальных дискретных исхода, вероятность каждого исхода находится в диапазоне от 0 до 1, а сумма вероятностей равна 1:
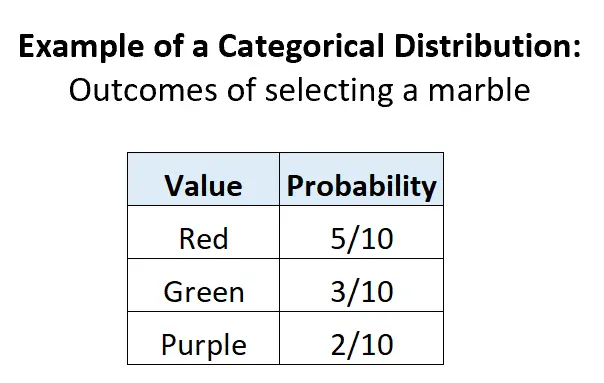
Пример 2: Выбор шариков в урне.
Предположим, в урне лежат 5 красных шариков, 3 зеленых шарика и 2 фиолетовых шарика. Если мы случайным образом выберем шар из урны, то существует 3 возможных дискретных исхода, вероятность каждого исхода находится в диапазоне от 0 до 1, а сумма вероятностей равна 1:
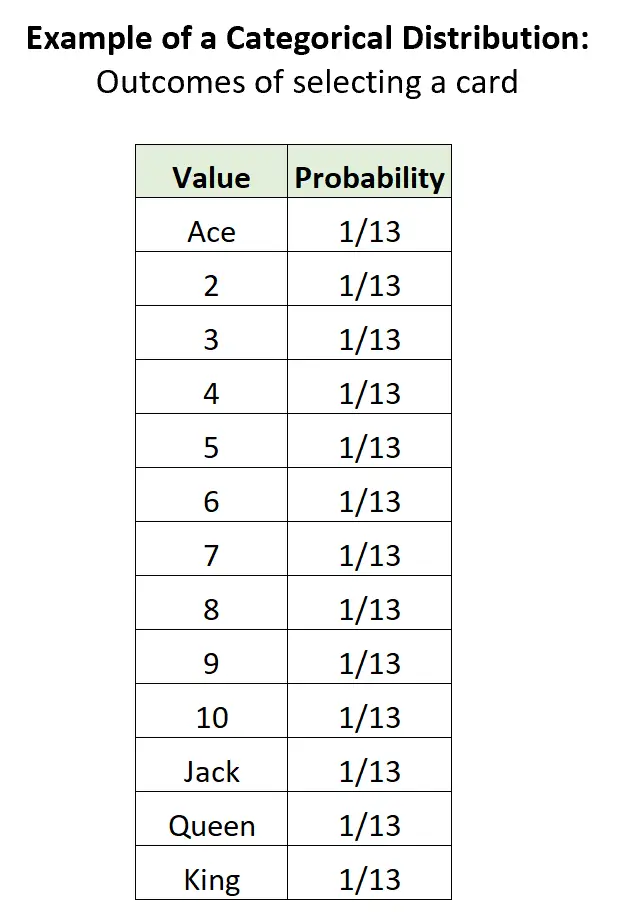
Пример 3: Выбор карты из колоды.
Если мы случайным образом выберем карту из стандартной колоды из 52 карт, то существует 13 потенциальных дискретных исходов, вероятность каждого исхода находится в диапазоне от 0 до 1, а сумма вероятностей равна 1:
Связь с другими дистрибутивами
Чтобы распределение можно было классифицировать как категориальное распределение , оно должно иметь K ≥ 2 потенциальных исходов и n = 1 испытание.
Используя эту терминологию, категориальное распределение похоже на следующие распределения:
Распределение Бернулли: K = 2 результата, n = 1 тест
Биномиальное распределение: K = 2 конечных точки, n ≥ 1 испытание.
Полиномиальное распределение: K ≥ 2 результатов, n ≥ испытания
Дополнительные ресурсы
Что такое случайные величины?
Введение в биномиальное распределение
Введение в полиномиальное распределение