Как выполнить квадратичную регрессию в python
Квадратичная регрессия — это тип регрессии, который мы можем использовать для количественной оценки связи между переменной-предиктором и переменной ответа, когда истинные отношения являются квадратичными, что может выглядеть на графике как буква «U» или перевернутая буква «U».
То есть, когда переменная-предиктор увеличивается, переменная ответа также имеет тенденцию увеличиваться, но после определенного момента переменная ответа начинает уменьшаться, поскольку переменная-предиктор продолжает увеличиваться.
В этом руководстве объясняется, как выполнить квадратичную регрессию в Python.
Пример: квадратичная регрессия в Python
Предположим, у нас есть данные о количестве отработанных часов в неделю и уровне счастья (по шкале от 0 до 100) для 16 разных людей:
import numpy as np import scipy.stats as stats #define variables hours = [6, 9, 12, 12, 15, 21, 24, 24, 27, 30, 36, 39, 45, 48, 57, 60] happ = [12, 18, 30, 42, 48, 78, 90, 96, 96, 90, 84, 78, 66, 54, 36, 24]
Если мы построим простую диаграмму рассеяния этих данных, мы увидим, что связь между двумя переменными имеет форму буквы «U»:
import matplotlib.pyplot as plt
#create scatterplot
plt.scatter(hours, happ)
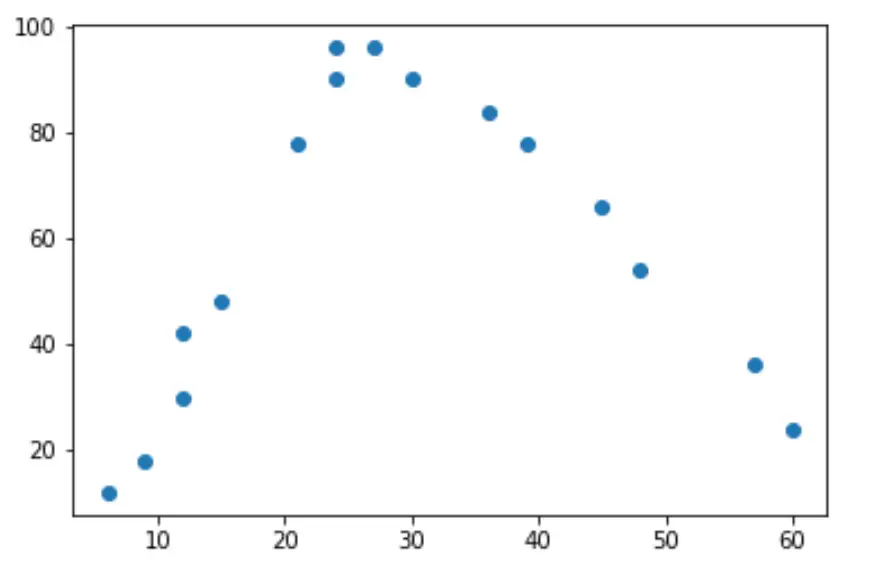
По мере увеличения количества отработанных часов счастье также увеличивается, но как только количество отработанных часов превышает 35 часов в неделю, счастье начинает снижаться.
Из-за U-образной формы это означает, что квадратичная регрессия, вероятно, является хорошим кандидатом для количественной оценки связи между двумя переменными.
Чтобы фактически выполнить квадратичную регрессию, мы можем подогнать модель полиномиальной регрессии со степенью 2, используя функцию numpy.polyfit() :
import numpy as np #polynomial fit with degree = 2 model = np.poly1d(np.polyfit(hours, happ, 2)) #add fitted polynomial line to scatterplot polyline = np.linspace(1, 60, 50) plt.scatter(hours, happ) plt.plot(polyline, model(polyline)) plt.show()
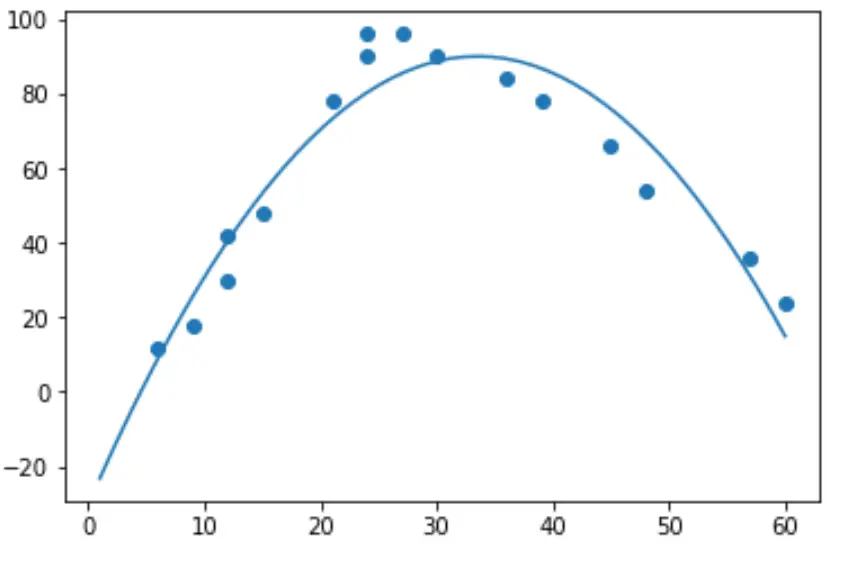
Мы можем получить уравнение полиномиальной регрессии, распечатав коэффициенты модели:
print (model)
-0.107x 2 + 7.173x - 30.25
Подобранное уравнение квадратичной регрессии:
Счастье = -0,107(часы) 2 + 7,173(часы) – 30,25
Мы можем использовать это уравнение, чтобы рассчитать ожидаемый уровень счастья человека на основе отработанного им времени. Например, ожидаемый уровень счастья человека, работающего 30 часов в неделю, составляет:
Счастье = -0,107(30) 2 + 7,173(30) – 30,25 = 88,64 .
Мы также можем написать короткую функцию, чтобы получить R-квадрат модели, который представляет собой долю дисперсии переменной отклика, которую можно объяснить переменными-предикторами.
#define function to calculate r-squared def polyfit(x, y, degree): results = {} coeffs = np.polyfit(x, y, degree) p = np.poly1d(coeffs) #calculate r-squared yhat = p(x) ybar = np.sum(y)/len(y) ssreg = np.sum((yhat-ybar)**2) sstot = np.sum((y - ybar)**2) results['r_squared'] = ssreg / sstot return results #find r-squared of polynomial model with degree = 3 polyfit(hours, happ, 2) {'r_squared': 0.9092114182131691}
В этом примере квадрат R модели равен 0,9092 .
Это означает, что 90,92% изменений в зарегистрированных уровнях счастья можно объяснить переменными-предикторами.
Дополнительные ресурсы
Как выполнить полиномиальную регрессию в Python
Как выполнить квадратичную регрессию в R
Как выполнить квадратичную регрессию в Excel