Как выполнить квантильную регрессию в r

Линейная регрессия — это метод, который мы можем использовать, чтобы понять взаимосвязь между одной или несколькими переменными-предикторами и переменной отклика .

Обычно, когда мы выполняем линейную регрессию, мы хотим оценить среднее значение переменной ответа.

Однако вместо этого мы могли бы использовать метод, известный как квантильная регрессия , для оценки любого значения квантиля или процентиля значения ответа, например 70-го процентиля, 90-го процентиля, 98-го процентиля и т. д.

Чтобы выполнить квантильную регрессию в R, мы можем использовать функцию rq() из пакета quantreg , которая использует следующий синтаксис:

 library (quantreg)

model <- rq(y ~ x, data = dataset, tau = 0.5 )

Золото:

• y: переменная ответа
• x: прогнозируемая переменная(и)
• данные: имя набора данных
• тау: процентиль, который нужно найти. По умолчанию используется медиана (tau = 0,5), но вы можете установить любое число от 0 до 1.

В этом руководстве представлен пошаговый пример использования этой функции для выполнения квантильной регрессии в R.

Шаг 1: Введите данные

В этом примере мы создадим набор данных, содержащий учебные часы и результаты экзаменов, полученные для 100 разных студентов университета:

 #make this example reproducible
set.seed(0)

#create data frame 
hours <- runif(100, 1, 10)
score <- 60 + 2*hours + rnorm(100, mean=0, sd=.45*hours)
df <- data.frame(hours, score)

#view first six rows
head(df)

     hours score
1 9.070275 79.22682
2 3.389578 66.20457
3 4.349115 73.47623
4 6.155680 70.10823
5 9.173870 78.12119
6 2.815137 65.94716

Шаг 2. Выполните квантильную регрессию

Далее мы подберем модель квантильной регрессии, используя часы обучения в качестве предикторной переменной и результаты экзаменов в качестве переменной ответа.

Мы будем использовать модель для прогнозирования ожидаемого 90-го процентиля результатов экзамена на основе количества изученных часов:

 library (quantreg)

#fit model
model <- rq(score ~ hours, data = df, tau = 0.9 )

#view summary of model
summary(model)

Call: rq(formula = score ~ hours, tau = 0.9, data = df)

tau: [1] 0.9

Coefficients:
            coefficients lower bd upper bd
(Intercept) 60.25185 59.27193 62.56459
hours 2.43746 1.98094 2.76989

Из результата мы можем увидеть предполагаемое уравнение регрессии:

Оценка экзамена по 90-му процентилю = 60,25 + 2,437*(часы)

Например, 90-й процентиль для всех студентов, обучающихся 8 часов, должен составлять 79,75:

90-й процентиль экзаменационного балла = 60,25 + 2,437*(8) = 79,75 .

Выходные данные также отображают верхний и нижний доверительные пределы для точки пересечения и времени переменной-предиктора.

Шаг 3. Визуализируйте результаты

Мы также можем визуализировать результаты регрессии, создав диаграмму рассеяния с подобранным уравнением квантильной регрессии, наложенным на график:

 library (ggplot2)

#create scatterplot with quantile regression line
ggplot(df, aes(hours,score)) +
  geom_point() + 
  geom_abline(intercept= coef (model)[1], slope= coef (model)[2]) 

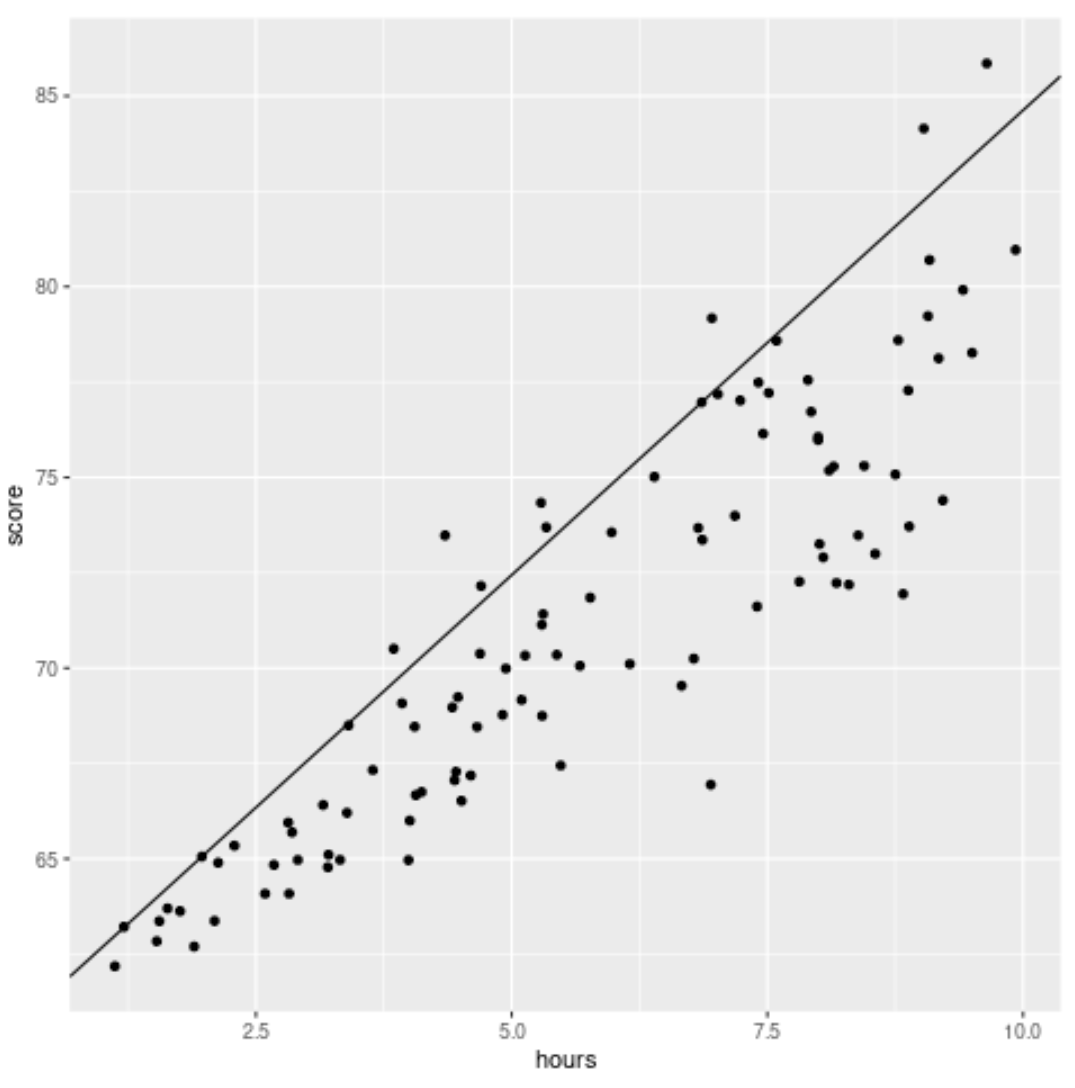
В отличие от традиционной линии линейной регрессии, обратите внимание, что эта подобранная линия не проходит через сердцевину данных. Вместо этого он проходит через расчетный 90-й процентиль на каждом уровне предикторной переменной.

Мы можем увидеть разницу между подобранным уравнением квантильной регрессии и простым уравнением линейной регрессии, добавив аргумент geom_smooth() :

 library (ggplot2)

#create scatterplot with quantile regression line and simple linear regression line
ggplot(df, aes(hours,score)) +
  geom_point() + 
  geom_abline(intercept= coef (model)[1], slope= coef (model)[2]) +
  geom_smooth(method=" lm ", se= F ) 

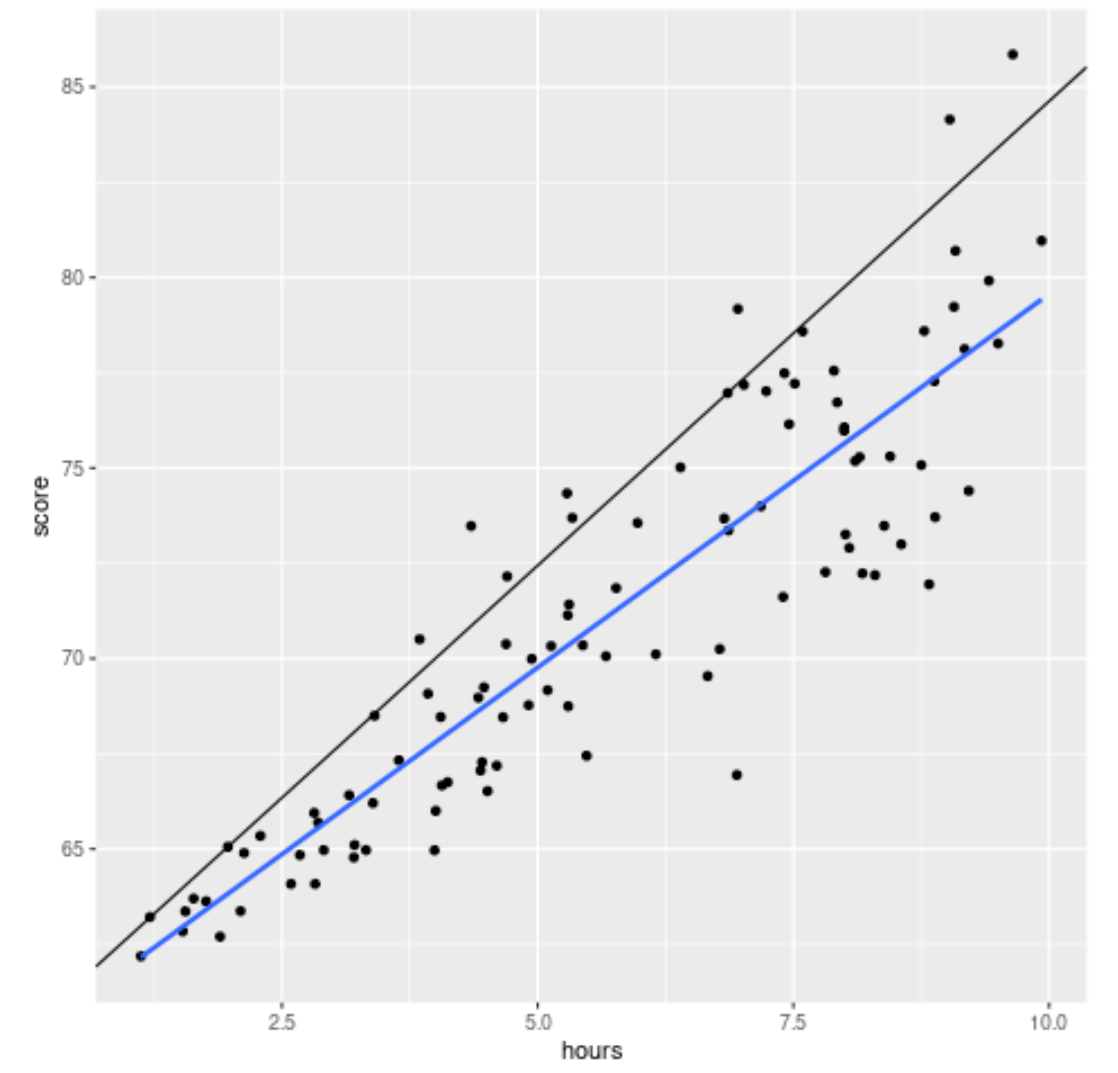
Черная линия отображает линию квантильной регрессии, скорректированную для 90-го процентиля, а синяя линия отображает линию простой линейной регрессии, которая оценивает среднее значение переменной ответа.

Как и ожидалось, простая линия линейной регрессии проходит через данные и показывает нам расчетное среднее значение баллов экзамена на каждом уровне часов.

Дополнительные ресурсы

В следующих руководствах объясняется, как выполнять другие распространенные задачи в R:

Как выполнить простую линейную регрессию в R
Как выполнить множественную линейную регрессию в R
Как выполнить квадратичную регрессию в R