Как рассчитать квартили для сгруппированных данных
Квартили — это значения, которые делят набор данных на четыре равные части.
Вы можете использовать следующую формулу для расчета квартилей для сгруппированных данных:
Q i = L + (C/F) * (iN/4 – M)
Золото:
- L : Нижняя граница интервала, содержащего i- й квартиль.
- C : Ширина класса
- F : частота интервала, содержащего i- й квартиль.
- N : Общая частота
- M : совокупная частота, ведущая к интервалу, содержащему i- й квартиль.
Следующий пример показывает, как использовать эту формулу на практике.
Пример: расчет квартилей для сгруппированных данных
Предположим, у нас есть следующее распределение частот:
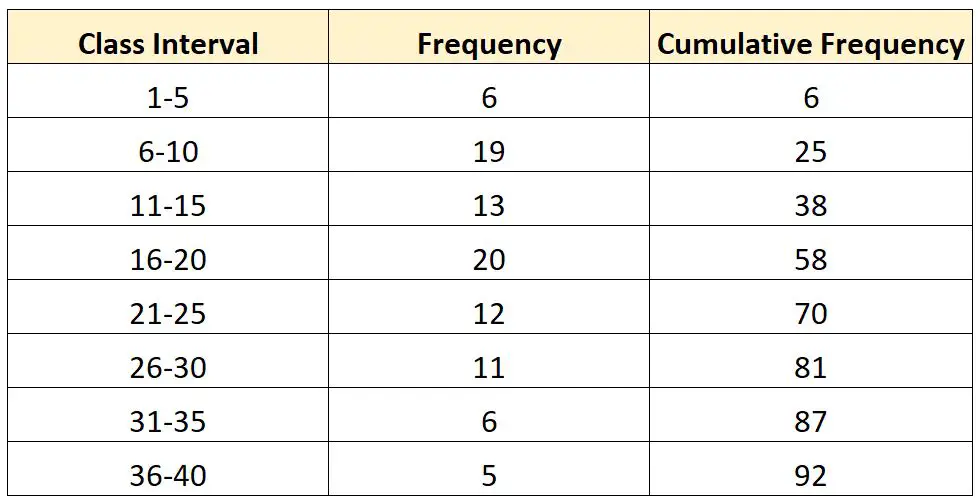
Теперь предположим, что мы хотим вычислить значение в третьем квартиле (Q 3 ) этого распределения.
Значение третьего квартиля будет расположено в позиции (iN/4) в распределении.
Итак, (iN/4) = (3*92/4) = 69.
Интервалом, содержащим третий квартиль, будет интервал 21–25 , поскольку 69 лежит между совокупными частотами 58 и 70.
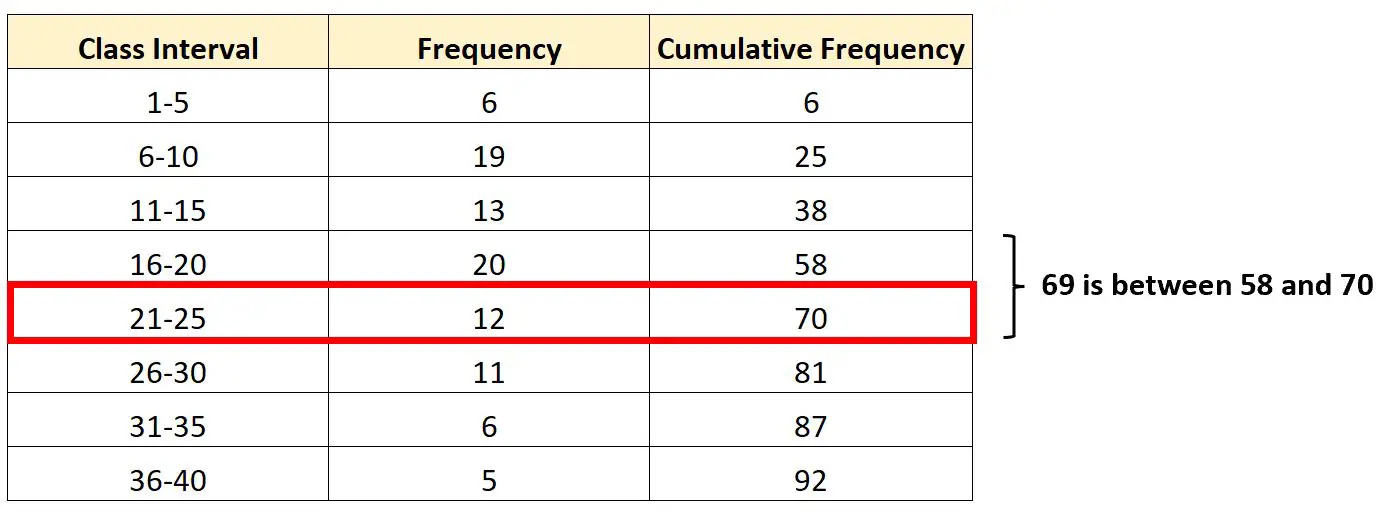
Зная это, мы можем найти каждое из необходимых значений для подстановки в нашу формулу:
L : Нижняя граница интервала, содержащего i- й квартиль.
- Нижняя граница интервала равна 21 .
C : Ширина класса
- Ширина класса рассчитывается следующим образом: 25 – 21 = 4 .
F : частота интервала, содержащего i- й квартиль.
- Частота 21-25 класса – 12.
N : Общая частота
- Общая совокупная частота в таблице равна 92 .
M : совокупная частота, ведущая к интервалу, содержащему i- й квартиль.
- Суммарная частота до 21-25 класса равна 58 .
Затем мы можем подставить все эти значения в предыдущую формулу, чтобы найти значение в третьем квартиле:
- Q i = L + (C/F) * (iN/4 – M)
- Q 3 = 21 + (4/12) * ((3)(92)/4 – 58)
- 3 квартал = 24,67
Значение в третьем квартиле составляет 24,67 .
Аналогичный подход можно использовать для расчета значений первого и второго квартиля.
Дополнительные ресурсы
В следующих руководствах представлена дополнительная информация о работе с сгруппированными данными:
Как найти среднее и стандартное отклонение сгруппированных данных
Как найти режим сгруппированных данных
Как найти медиану сгруппированных данных
Сгруппированные или несгруппированные распределения частот