Как создать ковариационную матрицу в python
Ковариация — это мера того, как изменения одной переменной связаны с изменениями второй переменной. Более конкретно, это мера степени линейной связи двух переменных.
Ковариационная матрица — это квадратная матрица, показывающая ковариацию между множеством различных переменных. Это может быть полезным способом понять, как различные переменные связаны в наборе данных.
В следующем примере показано, как создать ковариационную матрицу в Python.
Как создать ковариационную матрицу в Python
Используйте следующие шаги, чтобы создать ковариационную матрицу в Python.
Шаг 1: Создайте набор данных.
Сначала мы создадим набор данных, содержащий результаты тестов 10 разных учеников по трем предметам: математика, естествознание и история.
import numpy as np math = [84, 82, 81, 89, 73, 94, 92, 70, 88, 95] science = [85, 82, 72, 77, 75, 89, 95, 84, 77, 94] history = [97, 94, 93, 95, 88, 82, 78, 84, 69, 78] data = np.array([math, science, history])
Шаг 2: Создайте ковариационную матрицу.
Далее мы создадим ковариационную матрицу для этого набора данных с помощью функции numpy cov() , указав, что смещение = True , чтобы мы могли вычислить ковариационную матрицу совокупности.
np.cov(data, bias= True )
array([[ 64.96, 33.2, -24.44],
[33.2, 56.4, -24.1],
[-24.44, -24.1, 75.56]])
Шаг 3: Интерпретируйте ковариационную матрицу.
Значения по диагоналям матрицы — это просто дисперсии каждого предмета. Например:
- Разница оценок по математике составляет 64,96.
- Дисперсия оценок по естествознанию составляет 56,4.
- Историческая дисперсия баллов составляет 75,56.
Остальные значения матрицы представляют собой ковариации между разными субъектами. Например:
- Ковариация между оценками по математике и естественным наукам составляет 33,2.
- Ковариация между оценками по математике и истории составляет -24,44.
- Ковариация между оценками по естествознанию и истории составляет -24,1.
Положительное число ковариации указывает на то, что две переменные имеют тенденцию увеличиваться или уменьшаться одновременно. Например, математика и естествознание имеют положительную ковариацию (33,2), что указывает на то, что учащиеся, набравшие высокие баллы по математике, также имеют тенденцию получать высокие баллы по естественным наукам. И наоборот, учащиеся, которые плохо успевают по математике, также, как правило, плохо успевают по естественным наукам.
Отрицательное число ковариации указывает на то, что по мере увеличения одной переменной вторая переменная имеет тенденцию к уменьшению. Например, математика и история имеют отрицательную ковариацию (-24,44), что указывает на то, что учащиеся, набравшие высокие баллы по математике, как правило, получают низкие баллы по истории. И наоборот, учащиеся с низкими баллами по математике, как правило, получают высокие баллы по истории.
Шаг 4. Визуализируйте ковариационную матрицу (необязательно).
Вы можете визуализировать ковариационную матрицу, используя функцию Heatmap() пакета seaborn:
import seaborn as sns import matplotlib.pyplot as plt cov = np.cov(data, bias=True) labs = ['math', 'science', 'history'] sns.heatmap(cov, annot=True, fmt='g', xticklabels=labs, yticklabels=labs) plt.show()
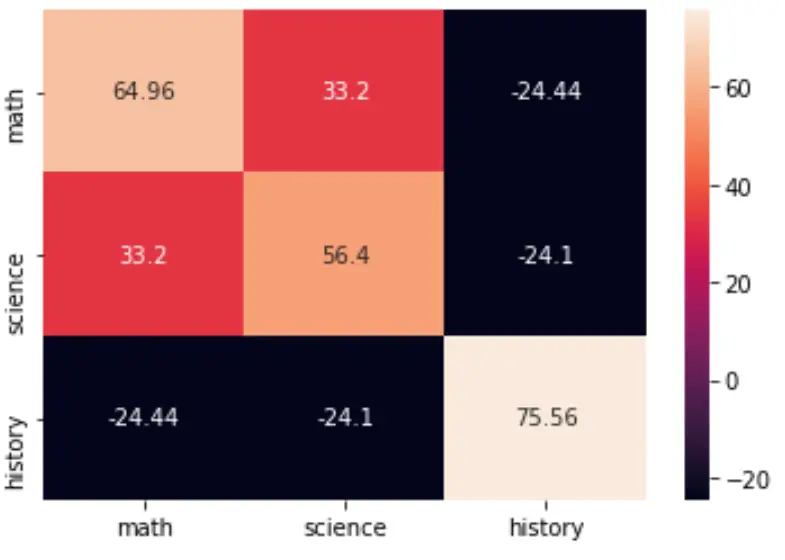
Вы также можете изменить цветовую палитру, указав аргумент cmap :
sns.heatmap(cov, annot=True, fmt='g', xticklabels=labs, yticklabels=labs, cmap=' YlGnBu ')
plt.show()
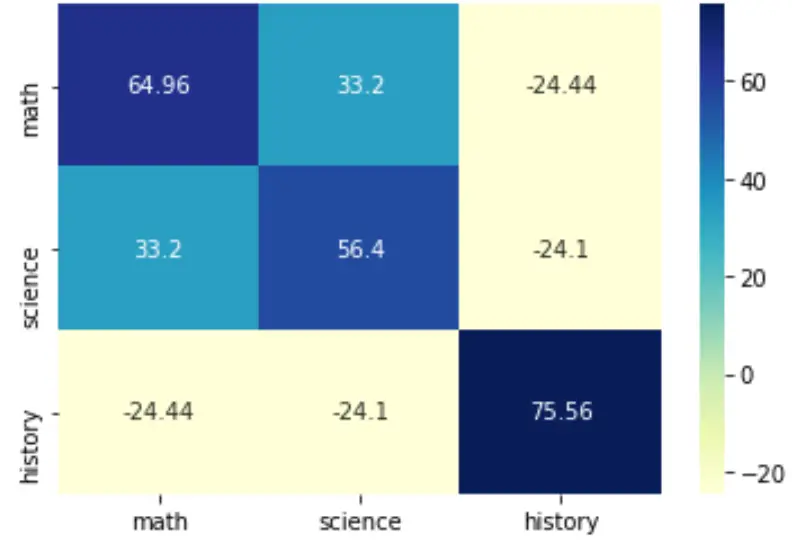
Более подробную информацию о том, как стилизовать эту тепловую карту, можно найти в документации seaborn .