Как создать ковариационную матрицу в spss

Ковариация — это мера того, как изменения одной переменной связаны с изменениями второй переменной. Более конкретно, это мера степени линейной связи двух переменных.

Формула для расчета ковариации между двумя переменными X и Y :

COV( X , Y ) = Σ(x- x )(y- y ) / n

Ковариационная матрица — это квадратная матрица, показывающая ковариацию между различными переменными в наборе данных.

В этом руководстве объясняется, как создать ковариационную матрицу для заданного набора данных в SPSS.

Пример: Ковариационная матрица в SPSS

Предположим, у нас есть следующий набор данных, который показывает результаты тестов 10 разных учеников по трем предметам: математика, естествознание и история:

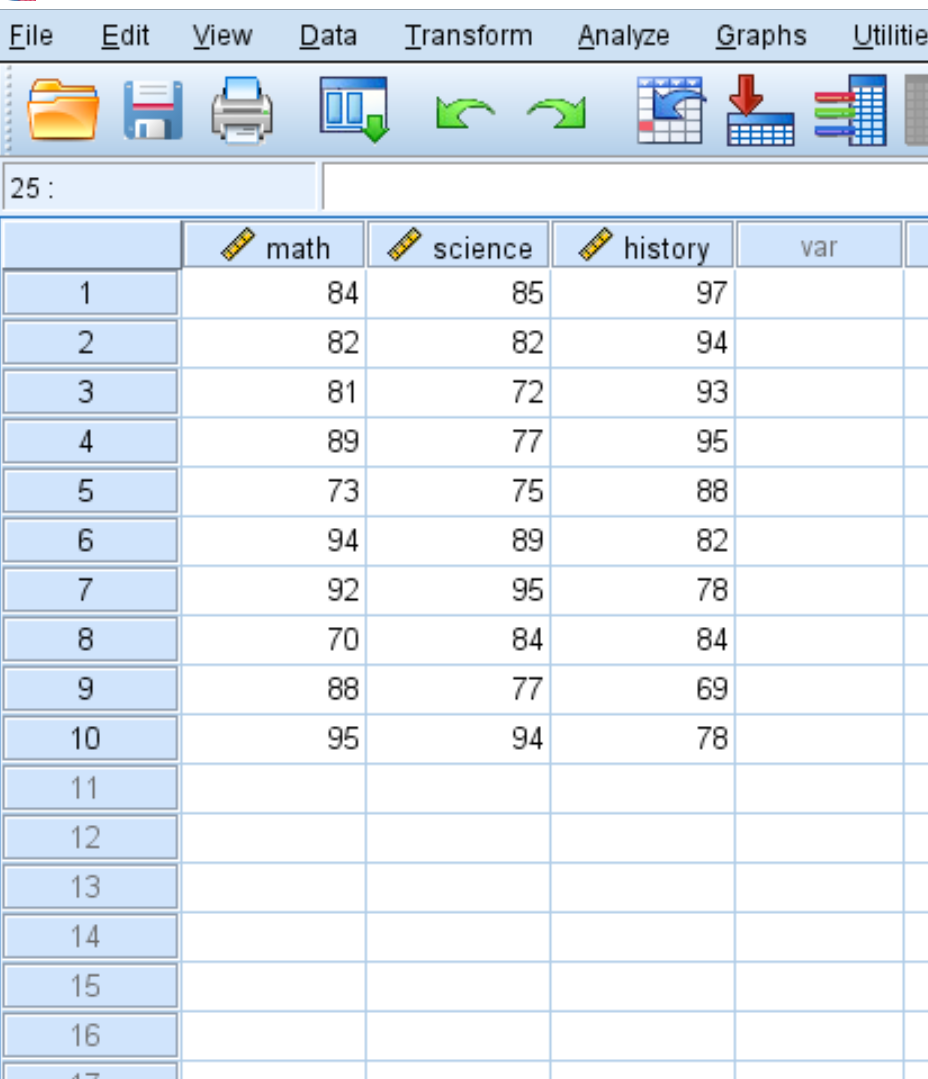
Чтобы создать ковариационную матрицу для этого набора данных, перейдите на вкладку «Анализ» , затем «Коррелировать» , затем «Двумерный» :

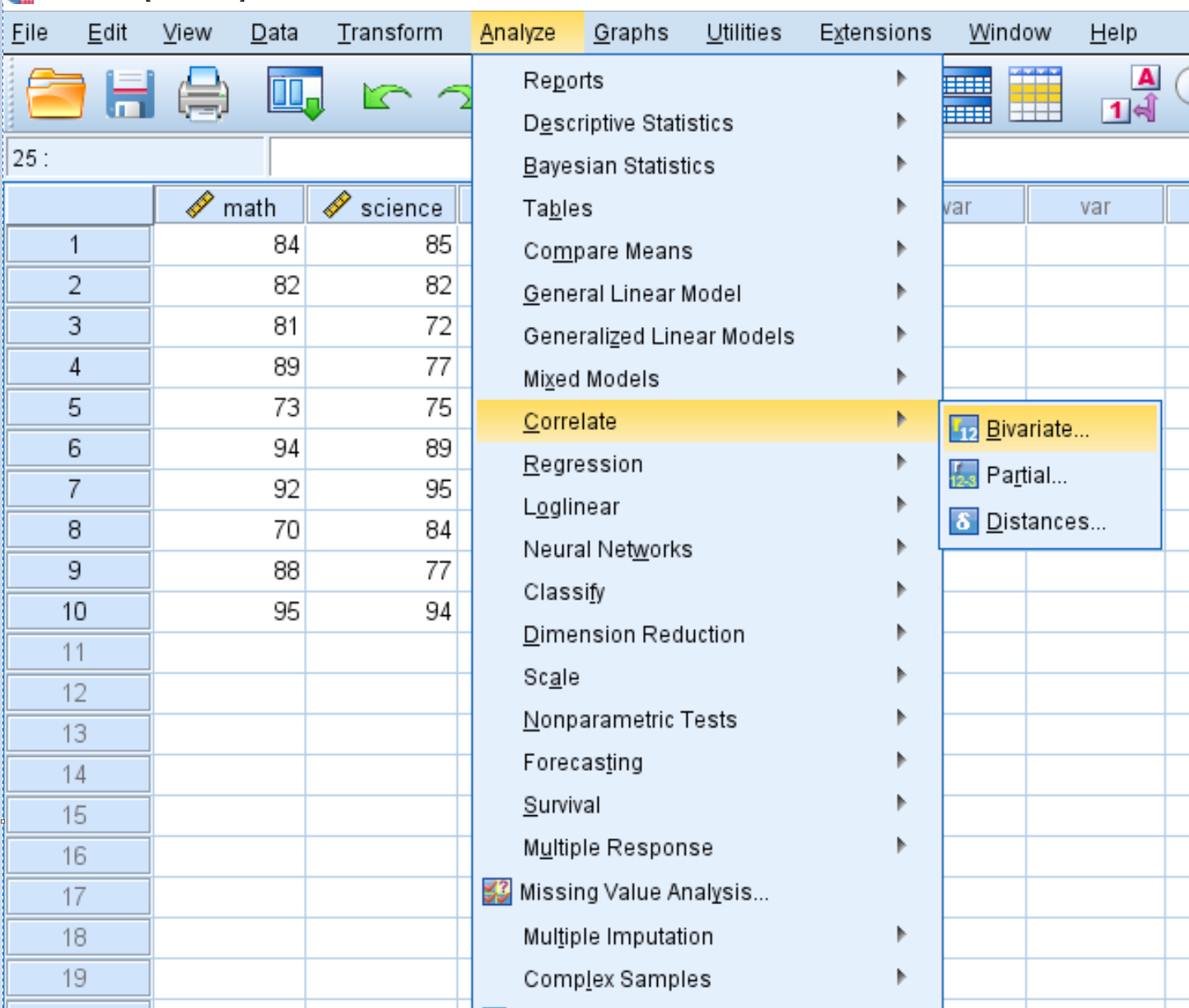
В появившемся новом окне перетащите каждую из трех переменных в поле с надписью «Переменные» :

Далее нажмите «Параметры» . Установите флажок рядом с пунктом «Отклонения и ковариации между продуктами» . Затем нажмите Продолжить .

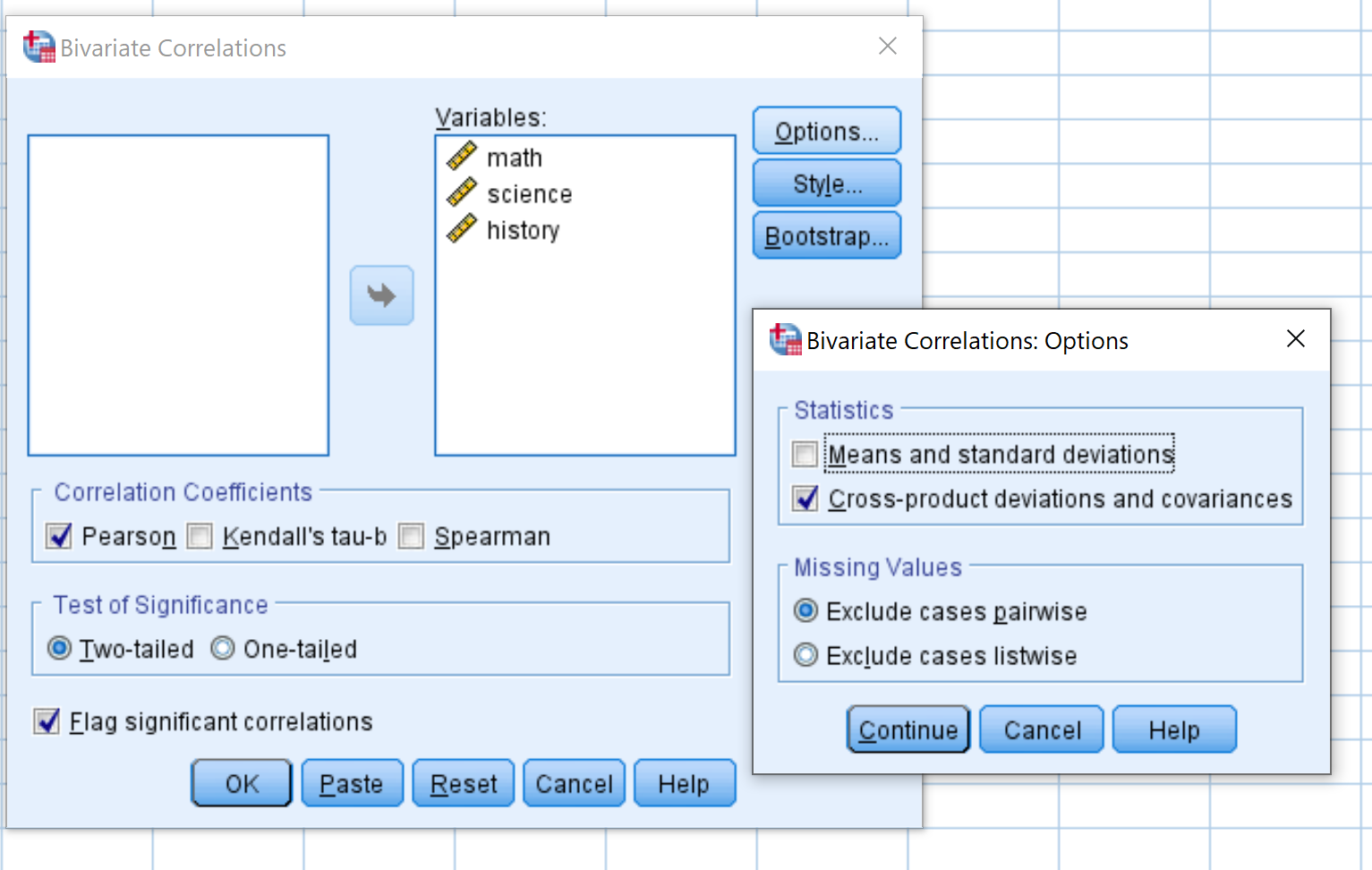
Затем нажмите ОК . Результат появится в новом окне:

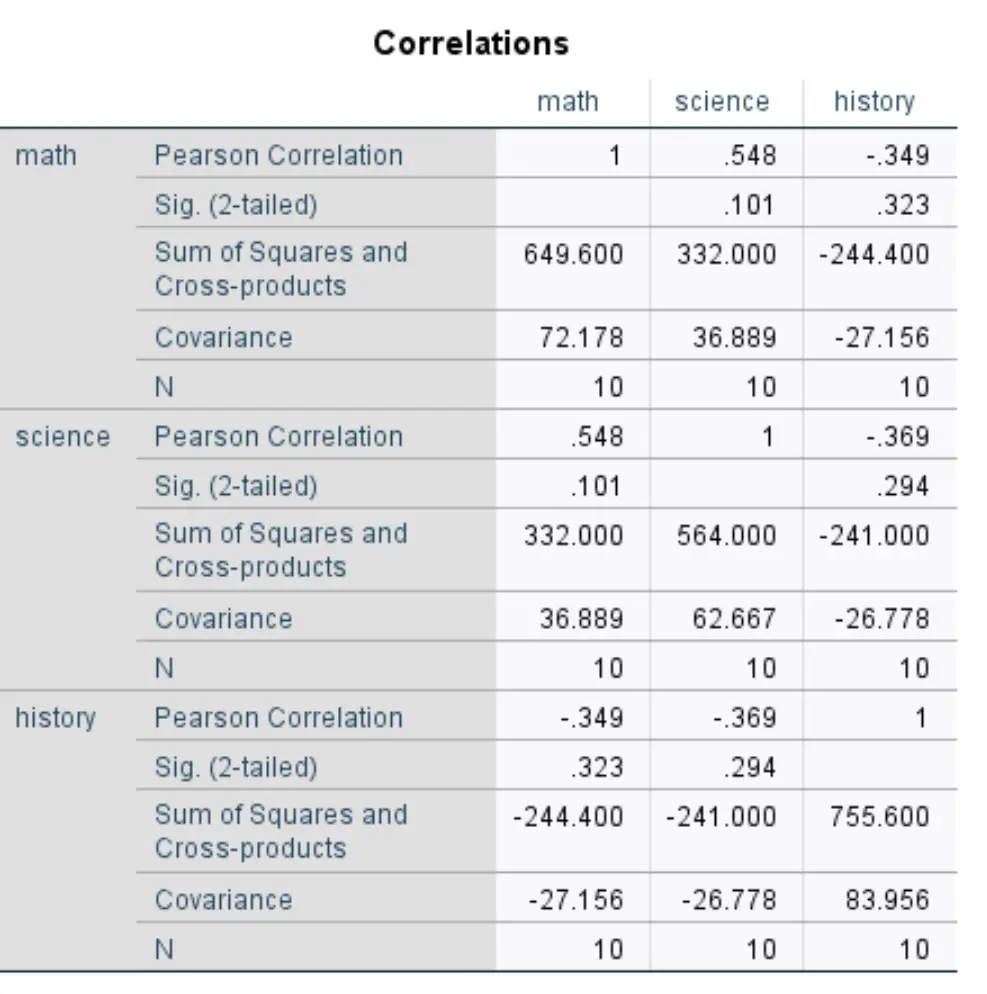
Чтобы получить ковариацию для каждой парной комбинации переменных, нужно разделить сумму квадратов и векторных произведений на N.

Например, ковариацию между математикой и естественными науками можно рассчитать следующим образом:

COV (математика, естественные науки) = 332 000/10 = 33,2 .

Аналогичным образом, ковариацию между математикой и историей можно рассчитать следующим образом:

COV (математика, история) = -244,400/10 = -24,44 .

Вы также можете получить дисперсию для каждой переменной, разделив сумму квадратов и векторных произведений на N.

Например, дисперсию по математике можно рассчитать следующим образом:

ВАР(математика) = 649,600/10 = 64,96 .

Вы можете получить полную ковариационную матрицу для этого набора данных, выполнив аналогичные вычисления:

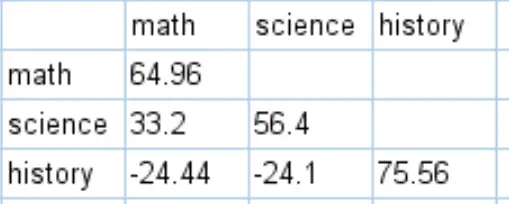
Как интерпретировать ковариационную матрицу

Значения по диагоналям ковариационной матрицы — это просто дисперсии каждого субъекта. Например:

• Дисперсия результатов математических вычислений составляет 64,96 .
• Дисперсия оценок по естествознанию составляет 56,4 .
• Дисперсия исторических оценок составляет 75,56 .

Остальные значения матрицы представляют собой ковариации между разными субъектами. Например:

• Ковариация между оценками по математике и естественным наукам составляет 33,2 .
• Ковариация между оценками по математике и истории составляет -24,44 .
• Ковариация между оценками по естествознанию и истории составляет -24,1 .

Положительное число ковариации указывает на то, что две переменные имеют тенденцию увеличиваться или уменьшаться одновременно. Например, математика и естествознание имеют положительную ковариацию (33,2), что указывает на то, что учащиеся, набравшие высокие баллы по математике, также имеют тенденцию получать высокие баллы по естественным наукам. Аналогично, учащиеся, которые плохо успевают по математике, также, как правило, плохо успевают по естественным наукам.

Отрицательное число ковариации указывает на то, что по мере увеличения одной переменной вторая переменная имеет тенденцию к уменьшению. Например, естествознание и история имеют отрицательную ковариацию (-24,1), что указывает на то, что учащиеся, набравшие высокие баллы по естествознанию, как правило, получают низкие баллы по истории. Аналогичным образом, студенты с низкими баллами по естествознанию, как правило, получают высокие баллы по истории.

Дополнительные ресурсы

Как создать матрицу корреляции в SPSS
Как рассчитать частичную корреляцию в SPSS