Когда следует использовать коробчатую диаграмму? (3 сценария)

Ящичковая диаграмма — это тип графика, на котором отображается пятизначная сводка набора данных, которая включает в себя:

• Минимальное значение
• Первый квартиль (25-й процентиль)
• Медианное значение
• Третий квартиль (75-й процентиль)
• Максимальное значение

Мы используем три простых шага для создания коробчатой диаграммы для любого набора данных:

• 1. Нарисуйте прямоугольник от первого до третьего квартиля.
• 2. Нарисуйте вертикальную линию посередине.
• 3. Нарисуйте «усы» квартилей к минимальному и максимальному значению.

Обычно мы создаем коробчатые диаграммы в одном из трех сценариев:

Сценарий 1. Визуализируйте распределение значений в наборе данных.

Ящиковая диаграмма позволяет нам быстро визуализировать распределение значений в наборе данных и увидеть, где расположены пять числовых сводных значений.

Сценарий 2: сравнить два или более дистрибутива.

Параллельные диаграммы позволяют нам визуализировать различия между двумя или более распределениями и сравнивать медианные значения и распределение значений между распределениями.

Сценарий 3: Выявление выбросов.

На коробчатых диаграммах выбросы обычно представляются крошечными кружками, выходящими за пределы каждого уса. Наблюдение определяется как выброс, если оно соответствует одному из следующих критериев:

• Наблюдение меньше Q1 – 1,5*(Межквартильный размах)
• Наблюдение превышает Q3 + 1,5*(межквартильный размах)

Создав коробчатую диаграмму, мы можем быстро увидеть, есть ли в распределении выбросы.

Следующие примеры показывают, как мы будем использовать коробчатую диаграмму в каждом сценарии.

Сценарий 1. Визуализируйте распределение значений в наборе данных.

Предположим, баскетбольный тренер хочет визуализировать распределение очков, набранных игроками его команды, и поэтому создает следующую коробчатую диаграмму:

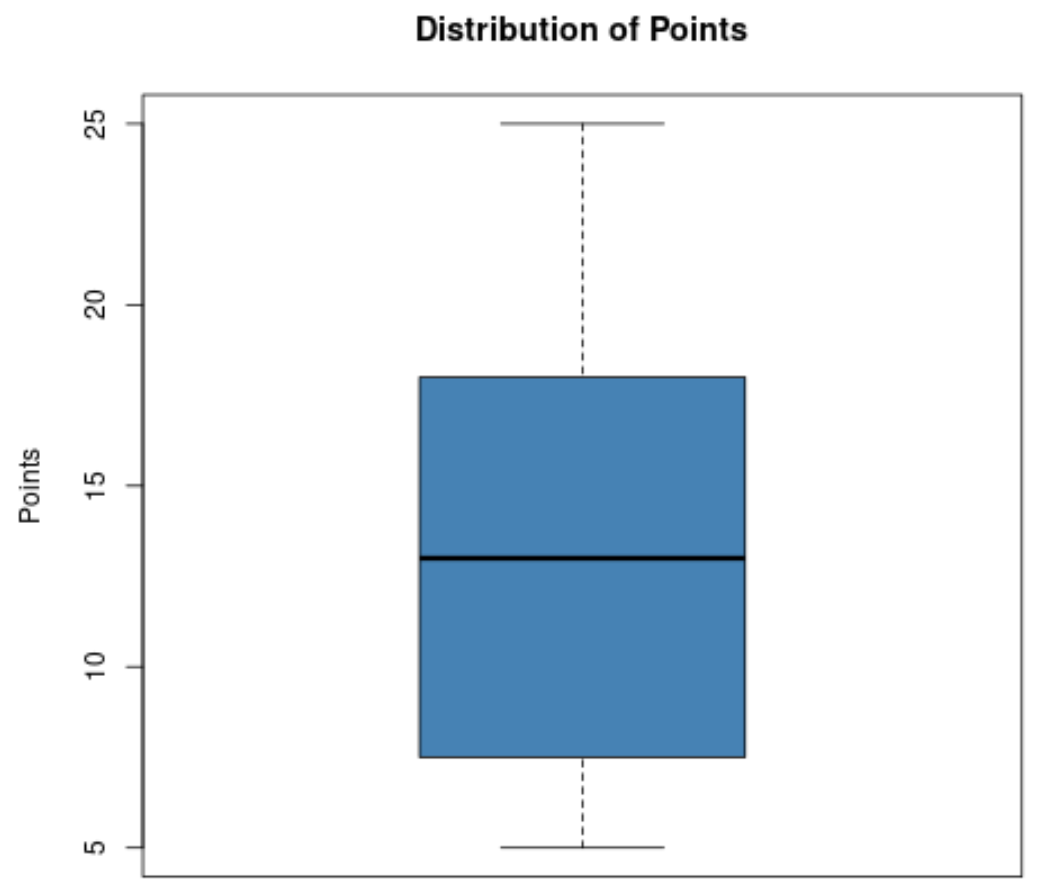
На основе этого коробчатого графика он может быстро увидеть следующие значения:

• Минимум: 5
• Т1 (первый квартиль): примерно 8
• Медиана: около 13
• Т3 (третий квартиль): примерно 18
• Максимум: 25

Это позволяет тренеру быстро увидеть, что очки, набранные игроками, варьируются от 5 до 25, что среднее количество набранных очков составляет примерно 13 и что 50% его игроков набирают от 8 до 18 очков за игру.

Сценарий 2. Сравните два или более дистрибутива.

Предположим, спортивный аналитик хочет сравнить распределение очков, набранных баскетболистами в трех разных командах, и создает следующие коробчатые диаграммы:

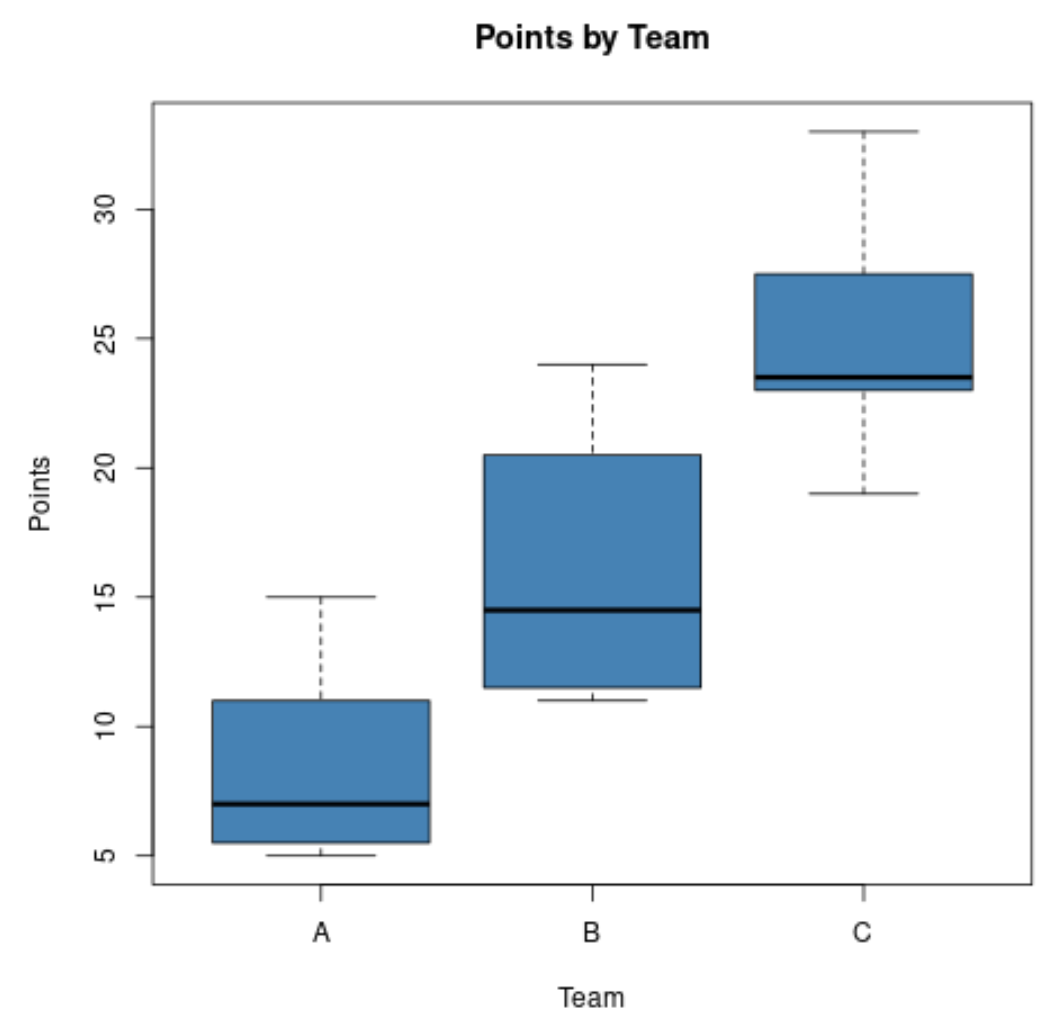
Используя эти графики, он может быстро увидеть, что у команды C самые высокие средние баллы, а у команды A самые низкие средние баллы.

Он также может быстро увидеть, что у команды Б самое большое распределение набранных очков, поскольку на коробчатой диаграмме команды Б самый длинный прямоугольник.

Сценарий 3: Выявление выбросов

Предположим, тренер по баскетболу хочет знать, не является ли один из его игроков исключением по количеству набранных очков. Он решает создать следующую коробчатую диаграмму, чтобы визуализировать распределение очков, набранных его игроками:

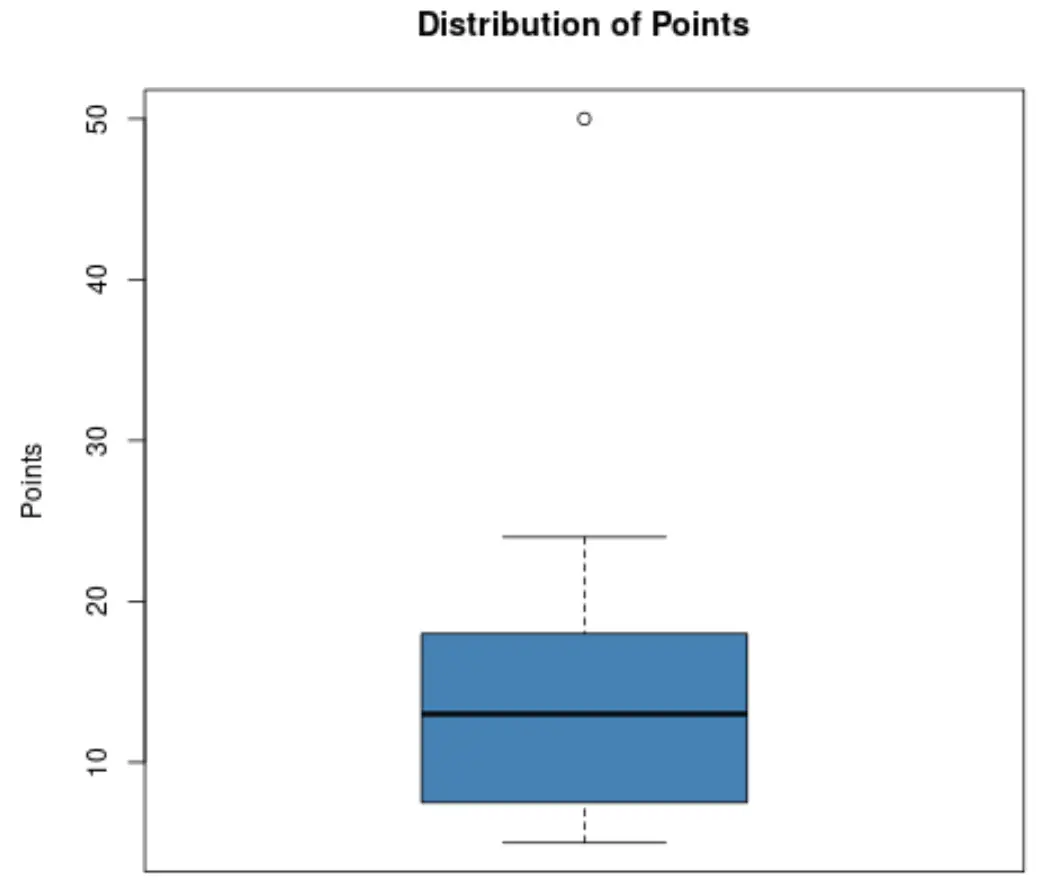
Используя этот график, тренер может видеть, что маленькая точка вверху графика указывает на выброс.

В частности, один из игроков набрал около 50 очков, что считается выбросом по сравнению со всеми остальными набранными очками.

Дополнительные ресурсы

Следующие руководства предлагают подробные объяснения того, как использовать коробчатые диаграммы на практике:

Как найти межквартильный диапазон (IQR) коробчатой диаграммы
Как определить асимметрию в коробчатых диаграммах
Как сравнивать коробчатые диаграммы

В следующих руководствах объясняется, как создавать коробчатые диаграммы в различных статистических программах:

Как создать коробчатую диаграмму в Google Sheets
Как создать коробчатые диаграммы в SPSS
Как создать параллельные прямоугольные диаграммы в Excel
Как создать параллельные прямоугольные диаграммы в R