Когда использовать ранговую корреляцию спирмена (2 сценария)

Самый распространенный способ количественной оценки линейной связи между двумя переменными — использовать коэффициент корреляции Пирсона , который всегда принимает значение от -1 до 1, где:

• -1 указывает на совершенно отрицательную линейную корреляцию.
• 0 указывает на отсутствие линейной корреляции
• 1 указывает на совершенно положительную линейную корреляцию.

Однако этот тип коэффициента корреляции работает лучше всего, когда истинная основная связь между двумя переменными является линейной .

Существует еще один тип коэффициента корреляции, называемый ранговой корреляцией Спирмена , который лучше всего использовать в двух конкретных сценариях:

Сценарий 1 : При работе с секретными данными.

• Примером может быть набор данных, содержащий рейтинг учащихся на экзамене по математике, а также рейтинг их баллов на экзамене по естественным наукам в классе.

Сценарий 2 : При наличии одного или нескольких крайних выбросов.

• Когда в наборе данных присутствуют экстремальные выбросы, это сильно влияет на коэффициент корреляции Пирсона.

Следующие примеры показывают, как рассчитать ранговую корреляцию Спирмена в каждом из этих сценариев.

Сценарий 1: Корреляция рейтинга Спирмена с ранжированными данными

Рассмотрим следующий набор данных (и соответствующую диаграмму рассеяния), который показывает взаимосвязь между двумя переменными:

Используя статистическое программное обеспечение, мы можем рассчитать следующие коэффициенты корреляции для этих двух переменных:

• Корреляция Пирсона: 0,79.
• Ранговая корреляция Спирмена: 1

В этом сценарии, если нас волнует только ранг значений данных (по мере увеличения ранга x увеличивается и ранг y?), то ранговая корреляция Спирмена дала бы нам лучшее представление о корреляция между двумя переменными. .

В этом конкретном наборе данных по мере увеличения ранга x всегда увеличивается ранг y.

Ранговая корреляция Спирмена прекрасно отражает это поведение, сообщая нам, что существует идеальная положительная связь ( ρ = 1 ) между рангами x и рангами y.

С другой стороны, корреляция Пирсона говорит нам, что между двумя переменными существует сильная линейная связь ( r = 0,79 ).

Это правда, но это бесполезно, если нас интересует только соотношение между рангами x и рангами y.

Сценарий 2: Корреляция рейтинга Спирмена с крайними выбросами

Рассмотрим следующий набор данных (и соответствующую диаграмму рассеяния), который показывает взаимосвязь между двумя переменными:

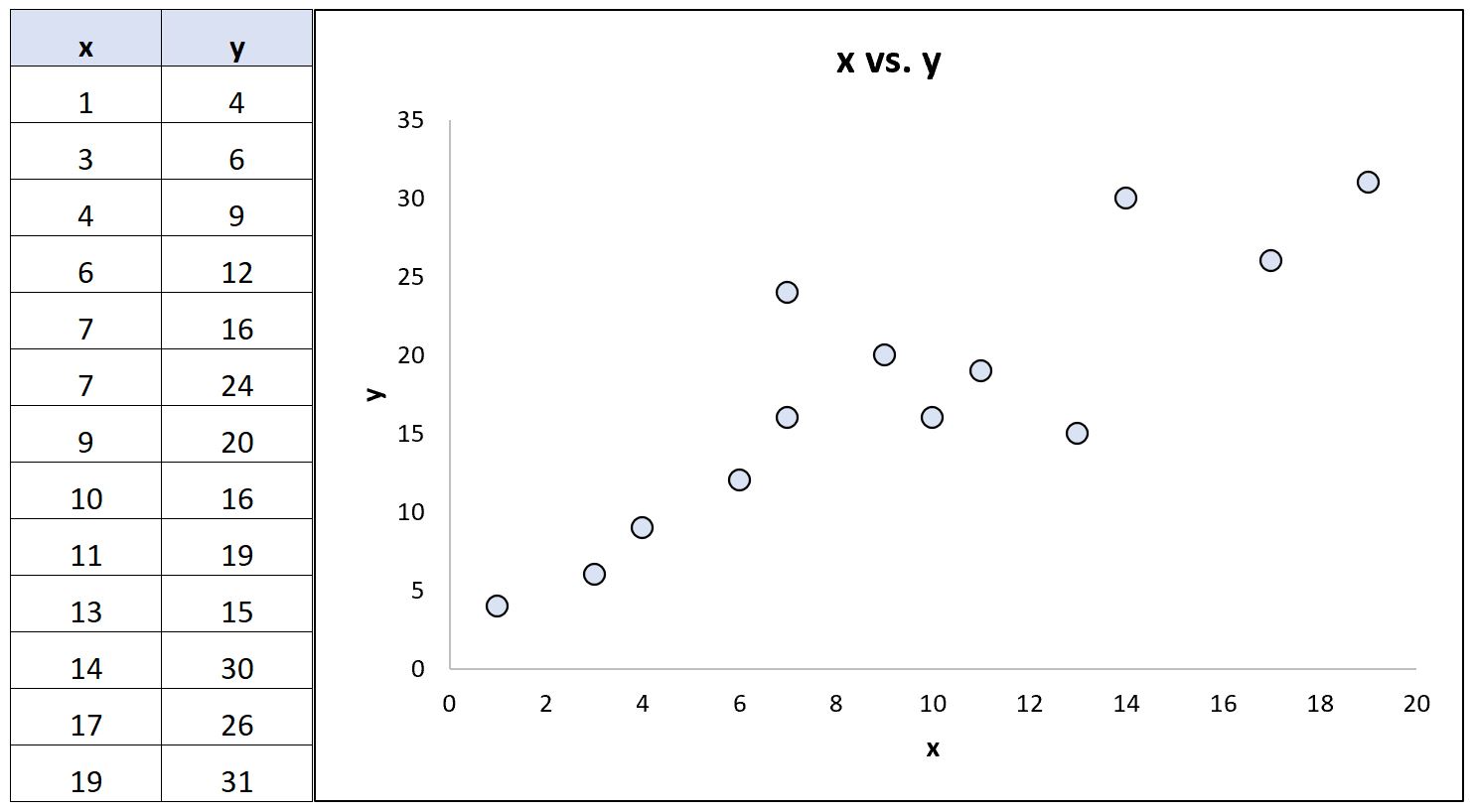
Используя статистическое программное обеспечение, мы можем рассчитать следующие коэффициенты корреляции для этих двух переменных:

• Корреляция Пирсона: 0,86
• Ранговая корреляция Спирмена: 0,85.

Коэффициенты корреляции практически идентичны, поскольку основная связь между переменными примерно линейна и нет резких выбросов.

Теперь предположим, что мы изменили последнее значение y в наборе данных так, чтобы оно стало экстремальным выбросом:

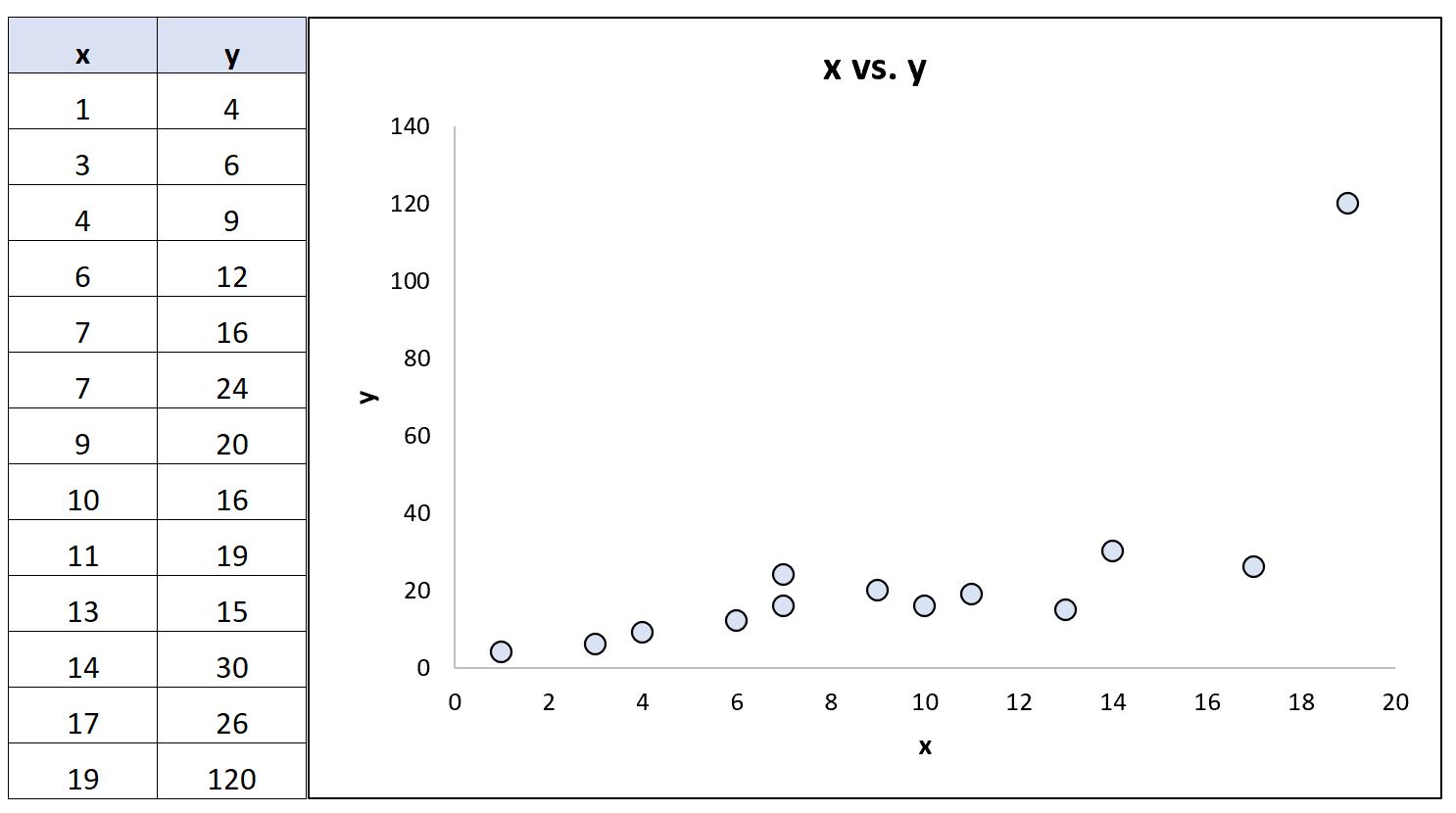
Используя статистическое программное обеспечение, мы можем пересчитать коэффициенты корреляции:

• Корреляция Пирсона: 0,69
• Ранговая корреляция Спирмена: 0,85.

Коэффициент корреляции Пирсона существенно изменился, тогда как коэффициент ранговой корреляции Спирмена остался прежним.

Используя статистический жаргон, мы бы сказали, что связь между x и y является монотонной (с увеличением x обычно увеличивается y), но не линейной, поскольку выброс сильно влияет на данные.

В этом сценарии ранговая корреляция Спирмена хорошо дает количественную оценку этой монотонной зависимости, тогда как корреляция Пирсона плохо справляется со своей задачей, поскольку пытается вычислить линейную связь между двумя переменными.

Связанный: Как сообщить о корреляции рангов Спирмена в формате APA

Дополнительные ресурсы

В следующих руководствах объясняется, как рассчитать ранговую корреляцию Спирмена с использованием различного программного обеспечения:

Как рассчитать корреляцию рангов Спирмена в Excel
Как рассчитать корреляцию рангов Спирмена в Google Таблицах
Как рассчитать ранговую корреляцию Спирмена в R
Как рассчитать корреляцию рангов Спирмена в Python