Каков компромисс между смещением и дисперсией в машинном обучении?
Чтобы оценить эффективность модели на наборе данных, нам необходимо измерить, насколько хорошо прогнозы модели соответствуют наблюдаемым данным.
Для регрессионных моделей наиболее часто используемой метрикой является среднеквадратическая ошибка (MSE), которая рассчитывается следующим образом:
MSE = (1/n)*Σ(y i – f(x i )) 2
Золото:
- n: общее количество наблюдений
- y i : Значение ответа i-го наблюдения.
- f(x i ): прогнозируемое значение ответа i- го наблюдения.
Чем ближе предсказания модели к наблюдениям, тем ниже будет MSE.
Однако нас интересует только тест MSE — MSE, когда наша модель применяется к невидимым данным. Это потому, что нас волнует только то, как модель будет работать с неизвестными данными, а не с существующими данными.
Например, это нормально, если модель, которая предсказывает цены на акции, имеет низкую MSE на исторических данных, но мы действительно хотим иметь возможность использовать эту модель для точного прогнозирования будущих данных.
Оказывается, тест MSE все же можно разбить на две части:
(1) Дисперсия: относится к величине, на которую изменилась бы наша функция f , если бы мы оценили ее с использованием другого обучающего набора.
(2) Смещение: относится к ошибке, вызванной подходом к реальной проблеме, которая может быть чрезвычайно сложной, с использованием гораздо более простой модели.
Записано математическими терминами:
Тест MSE = Var( f̂( x0 )) + [Смещение( f̂( x0 ))] 2 + Var(ε)
Тест MSE = дисперсия + смещение 2 + неустранимая ошибка
Третий член, неуменьшаемая ошибка, — это ошибка, которую не может уменьшить никакая модель просто потому, что во взаимоотношениях между набором объясняющих переменных и переменной отклика всегда присутствует шум .
Модели с высокой предвзятостью обычно имеют низкую дисперсию . Например, модели линейной регрессии, как правило, имеют высокую систематическую ошибку (предполагая простую линейную связь между объясняющими переменными и переменной отклика) и низкую дисперсию (оценки модели не будут сильно меняться от выборки к выборке). другой).
Однако модели с низким смещением, как правило, имеют высокую дисперсию . Например, сложные нелинейные модели, как правило, имеют низкую систематическую ошибку (не предполагают определенную взаимосвязь между объясняющими переменными и переменной отклика) и высокую дисперсию (оценки модели могут значительно меняться от одной выборки обучения к другой).
Компромисс смещения и дисперсии
Компромисс смещения и дисперсии относится к компромиссу, который имеет место, когда мы решаем уменьшить смещение, которое обычно увеличивает дисперсию, или уменьшить дисперсию, что обычно увеличивает смещение.
Следующий график предлагает способ визуализировать этот компромисс:
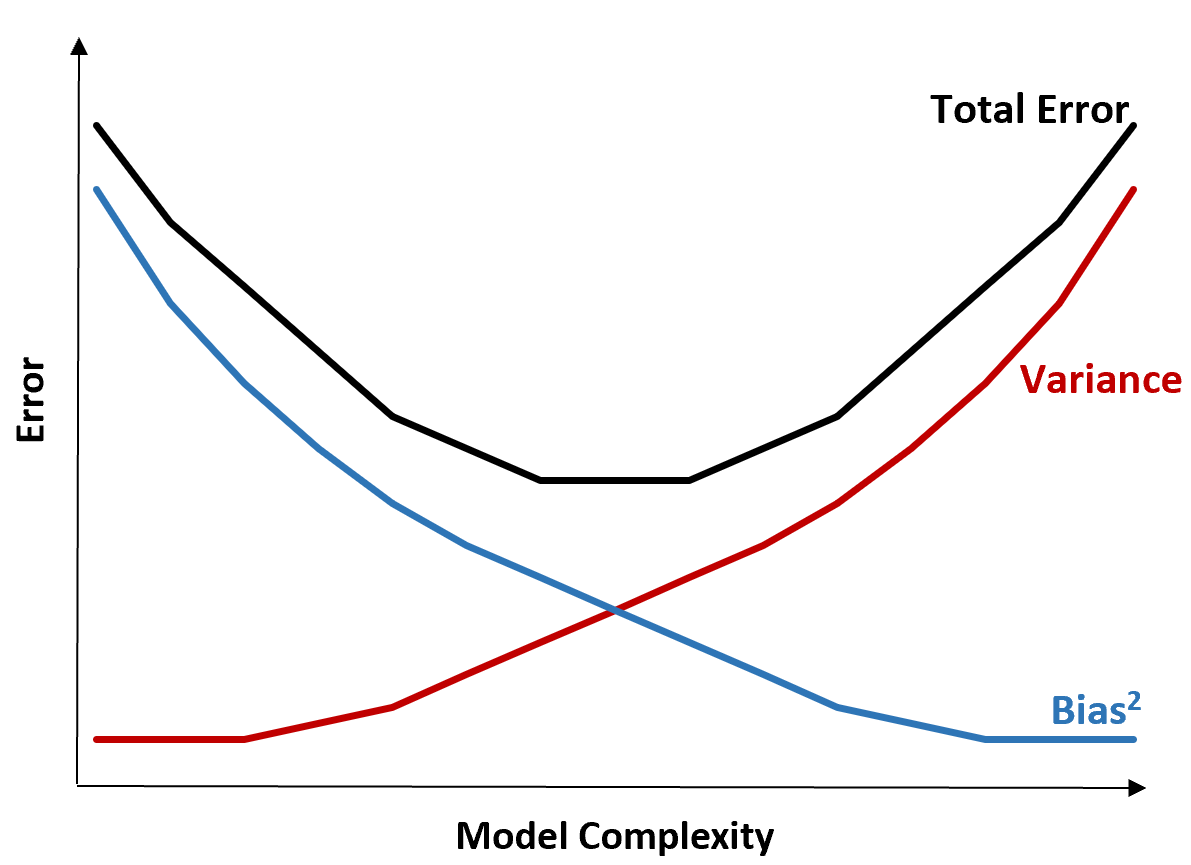
Суммарная ошибка уменьшается по мере увеличения сложности модели, но только до определенного момента. После определенной точки дисперсия начинает увеличиваться, и общая ошибка также начинает увеличиваться.
На практике нас заботит только минимизация общей ошибки модели, а не минимизация дисперсии или систематической ошибки. Оказывается, чтобы минимизировать общую ошибку, нужно найти правильный баланс между дисперсией и систематической погрешностью.
Другими словами, нам нужна модель, достаточно сложная, чтобы отразить истинную взаимосвязь между объясняющими переменными и переменной отклика, но не слишком сложная, чтобы обнаружить закономерности, которых на самом деле не существует.
Когда модель слишком сложна, она не соответствует данным. Это происходит потому, что слишком сложно найти в обучающих данных закономерности, вызванные просто случайностью. Этот тип модели, скорее всего, будет плохо работать с невидимыми данными.
Но когда модель слишком проста, она недооценивает данные. Это происходит потому, что предполагается, что истинная связь между объясняющими переменными и переменной отклика проще, чем есть на самом деле.
Способ выбора оптимальных моделей в машинном обучении — найти баланс между предвзятостью и дисперсией, чтобы минимизировать ошибку тестирования модели на будущих невидимых данных.
На практике наиболее распространенным способом минимизировать MSE тестов является использование перекрестной проверки .