Простое объяснение коррекции непрерывности в статистике
Коррекция непрерывности применяется, когда вы хотите использовать непрерывное распределение для аппроксимации дискретного распределения. Обычно он используется, когда вы хотите использовать нормальное распределение для аппроксимации биномиального распределения .
Напомним, что биномиальное распределение говорит нам о вероятности достижения успеха x в n испытаниях, учитывая, что вероятность успеха в одном испытании равна p . Чтобы ответить на вопросы о вероятности с помощью биномиального распределения, мы могли бы просто использовать калькулятор биномиального распределения , но мы также могли бы аппроксимировать вероятность, используя нормальное распределение с поправкой на непрерывность.
Коррекция непрерывности — это название операции добавления или вычитания 0,5 из дискретного значения x .
Например, предположим, что мы хотим найти вероятность того, что монета упадет орлом меньше или равна 45 раз в течение 100 бросков. То есть мы хотим найти P(X ≤ 45). Чтобы использовать нормальное распределение для аппроксимации биномиального распределения, вместо этого мы должны найти P (X ≤ 45,5).
В следующей таблице показано, когда следует прибавлять или вычитать 0,5, в зависимости от типа вероятности, которую вы пытаетесь найти:
| Используйте биномиальное распределение | Использование нормального распределения с коррекцией непрерывности |
|---|---|
| Х = 45 | 44,5 < Х < 45,5 |
| Х ≤ 45 | Х < 45,5 |
| Х < 45 | Х < 44,5 |
| Х ≥ 45 | Х > 44,5 |
| Х > 45 | Х > 45,5 |
Примечание:
Применять поправку на непрерывность к нормальному распределению для аппроксимации биномиального распределения уместно только тогда, когда n*p и n*(1-p) равны не менее 5.
Например, предположим, что n = 15 и p = 0,6. В этом случае:
п*р = 15 * 0,6 = 9
n*(1-p) = 15 * (1 – 0,6) = 15 * (0,4) = 6
Поскольку оба этих числа больше или равны 5, в этом сценарии было бы приемлемо применить поправку на непрерывность.
В следующем примере показано, как применить поправку на непрерывность к нормальному распределению для аппроксимации биномиального распределения.
Пример применения коррекции непрерывности
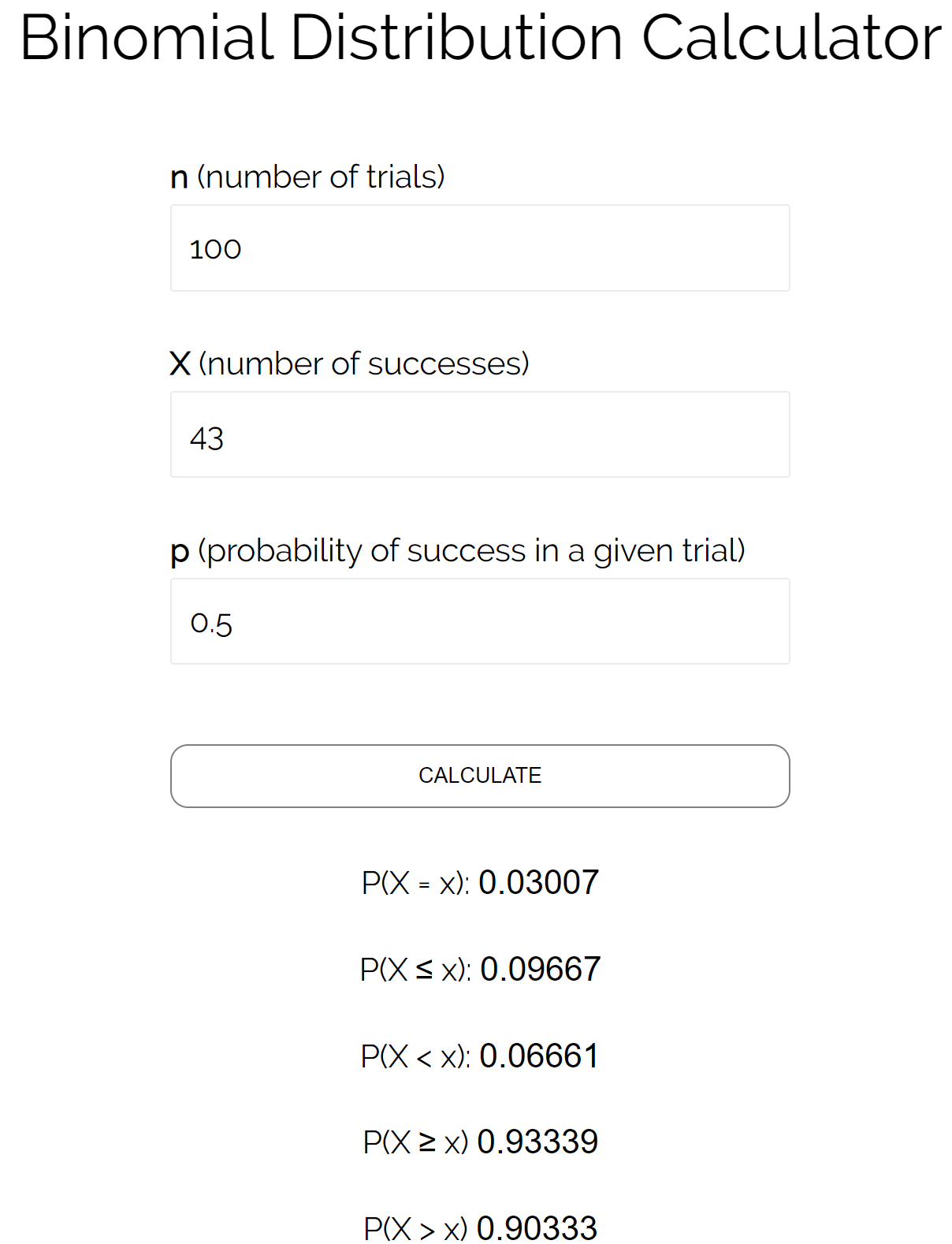
Предположим, мы хотим узнать вероятность того, что монета выпадет орлом меньше или равна 43 раза за 100 бросков. В этом случае:
n = количество испытаний = 100
X = количество успехов = 43
p = вероятность успеха в данном испытании = 0,50.
Мы можем подставить эти числа в калькулятор биномиального распределения и увидеть, что вероятность того, что монета выпадет орлом меньше или равна 43 раза, равна 0,09667 .
Чтобы аппроксимировать биномиальное распределение путем применения поправки на непрерывность к нормальному распределению, мы можем использовать следующие шаги:
Шаг 1. Убедитесь, что n*p и n*(1-p) равны не менее 5 .
н*р = 100*0,5 = 50
n*(1-p) = 100*(1 – 0,5) = 100*0,5 = 50
Оба числа больше или равны 5, поэтому мы можем продолжить.
Шаг 2. Определите, следует ли прибавлять или вычитать 0,5.
Обратившись к таблице выше, мы видим, что нам следует прибавлять 0,5 , когда мы работаем с вероятностью в виде X ≤ 43. Таким образом, мы найдем P(X< 43,5).
Шаг 3: Найдите среднее значение (μ) и стандартное отклонение (σ) биномиального распределения.
µ = n*p = 100*0,5 = 50
σ = √ n*p*(1-p) = √ 100*,5*(1-,5) = √ 25 = 5
Шаг 4. Найдите z-показатель, используя среднее значение и стандартное отклонение, найденные на предыдущем шаге.
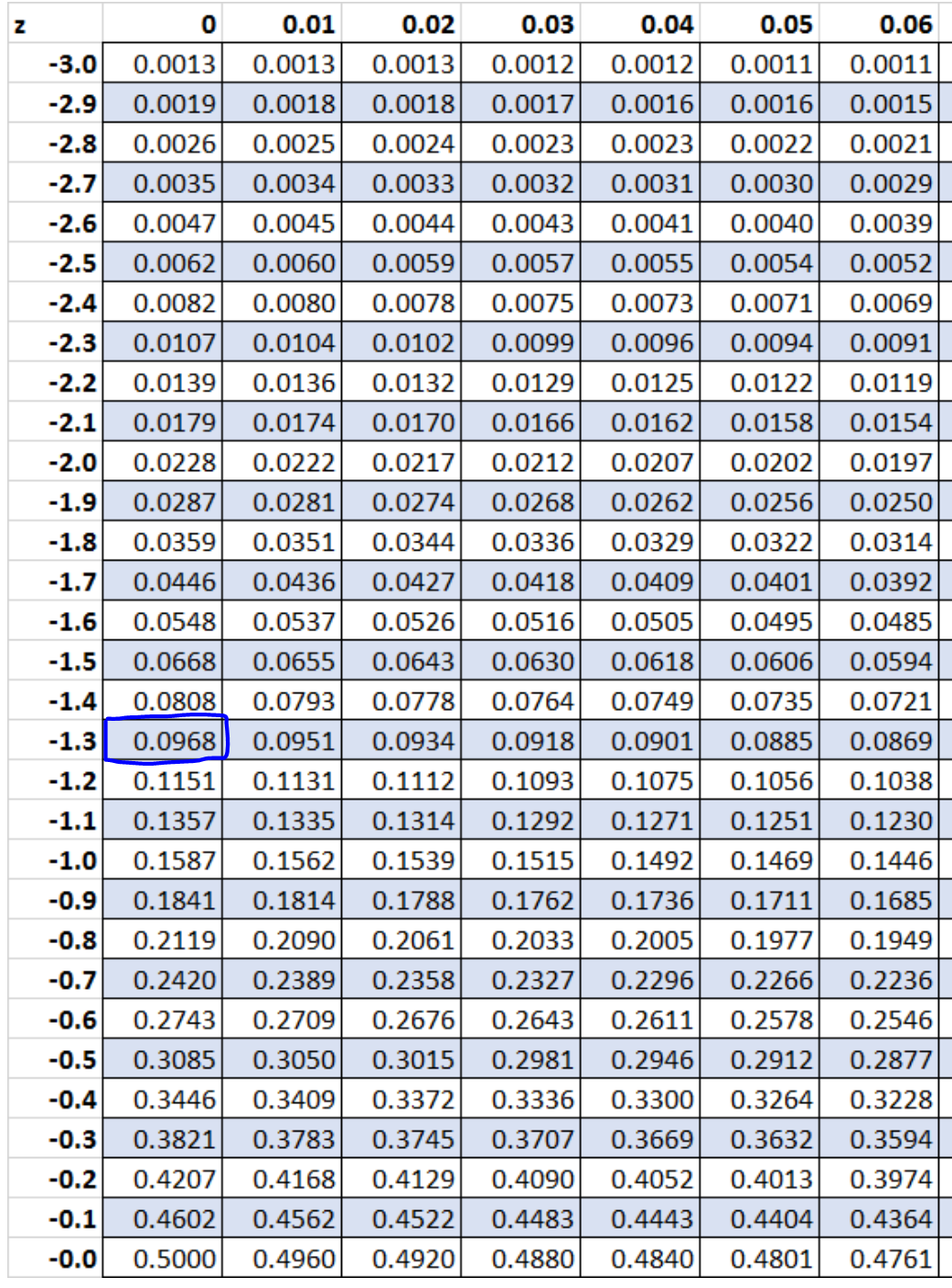
z = (x – µ)/σ = (43,5 – 50)/5 = -6,5/5 = -1,3.
Шаг 5. Используйте таблицу Z, чтобы найти вероятность, связанную с показателем z.
Согласно Таблице Z, вероятность, связанная с z = -1,3, равна 0,0968 .
Таким образом, точная вероятность, которую мы нашли с помощью биномиального распределения, составила 0,09667 , а приблизительная вероятность, которую мы нашли с помощью поправки на непрерывность с нормальным распределением, составила 0,0968 . Эти два значения достаточно близки.
Когда использовать коррекцию непрерывности
До того, как появилось современное статистическое программное обеспечение и расчеты приходилось выполнять вручную, поправки на непрерывность часто использовались для поиска вероятностей, связанных с дискретными распределениями. Сегодня поправки на непрерывность играют меньшую роль в вычислении вероятностей, поскольку мы обычно можем полагаться на программное обеспечение или калькуляторы, которые вычислят вероятности за нас.
Вместо этого это просто тема, рассматриваемая в курсах статистики, чтобы проиллюстрировать взаимосвязь между биномиальным распределением и нормальным распределением и показать, что нормальное распределение может аппроксимировать биномиальное распределение, применяя поправку на непрерывность.
Калькулятор коррекции непрерывности
Используйте калькулятор коррекции непрерывности , чтобы автоматически применять коррекцию непрерывности к нормальному распределению для аппроксимации биномиальных вероятностей.