Коррекция непрерывности йейта: определение и пример
Критерий независимости хи-квадрат используется для определения наличия значимой связи между двумя категориальными переменными.
В этом тесте используются следующие нулевые и альтернативные гипотезы:
- H 0 : (нулевая гипотеза) Обе переменные независимы.
- H 1 : (альтернативная гипотеза) Эти две переменные не являются независимыми. (т.е. они связаны)
Мы используем следующую формулу для расчета статистики теста Хи-квадрат x 2 для этого теста:
Икс 2 знак равно Σ(О я -Е я ) 2 / Е я
Золото:
- Σ: причудливый символ, означающий «сумма».
- O: наблюдаемое значение
- E: ожидаемое значение
Этот тест предполагает, что дискретные вероятности частот в таблице непредвиденных обстоятельств могут быть аппроксимированы распределением хи-квадрат, которое является непрерывным распределением.
Однако это предположение, как правило, несколько неверно, и результирующая статистика испытаний имеет тенденцию быть смещена в сторону повышения.
Чтобы исправить это смещение, мы можем применить поправку непрерывности Йейта , которая применяет следующую поправку к формуле X2 :
X 2 = Σ(|O i -E i | – 0,5) 2 / E i
Обычно мы используем эту поправку только в том случае, если хотя бы одна ячейка в таблице сопряженности имеет ожидаемую частоту менее 5.
Пример: применение поправки Йейта на непрерывность.
Предположим, мы хотим знать, связан ли пол с предпочтением той или иной политической партии. Мы берем простую случайную выборку из 40 избирателей и спрашиваем их об их предпочтениях в отношении политических партий. В следующей таблице представлены результаты опроса:

Вот как можно выполнить критерий независимости хи-квадрат с коррекцией непрерывности Йейта:
Наблюдаемые значения:

Ожидаемые значения:
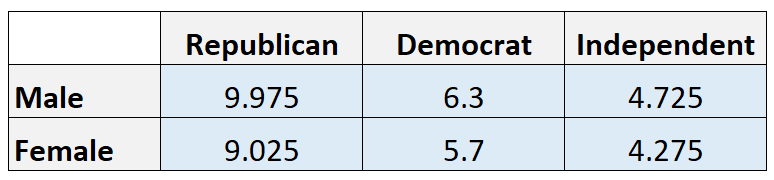
Примечание. Мы вычисляем ожидаемое значение в каждой ячейке, умножая сумму строки на сумму столбца, а затем разделяя на общую сумму. Например, ожидаемое количество мужчин-республиканцев составляет (21*19)/40 = 9,975.
Статистика теста хи — квадрат :
- (|8-9,975| – 0,5) 2 /9,975 = 0,218
- (|9-6,3| – 0,5) 2 /6,3 = 0,768
- (|4-4,725| – 0,5) 2 /4,725 = 0,011
- (|11-9,025| – 0,5) 2 /9,025 = 0,241
- (|3-5,7| – 0,5) 2 /5,7 = 0,849
- (|5-4,275| – 0,5) 2 /4,275 = 0,012
Итак ,
Значение P: Согласно калькулятору преобразования хи-квадрат в P-значение , значение p, соответствующее статистике теста хи-квадрат с 2 степенями свободы, составляет 0,3501 .
Поскольку это значение p не меньше 0,05, мы не сможем отвергнуть нулевую гипотезу. Это означает, что у нас нет достаточных доказательств, чтобы утверждать, что существует связь между полом и предпочтениями политических партий.