Как создать матрицу корреляции в sas (с примером)
Матрица корреляции представляет собой квадратную таблицу, в которой показаны коэффициенты корреляции между переменными в наборе данных.
Он обеспечивает быстрый способ понять силу линейных связей, существующих между переменными в наборе данных.
Вы можете использовать оператор PROC CORR в SAS для создания корреляционной матрицы для заданного набора данных:
/*create correlation matrix using all numeric variables in my_data*/
proc corr data =my_data;
run ;
По умолчанию будет создана матрица, отображающая коэффициенты корреляции между всеми числовыми переменными в наборе данных.
Чтобы включить в матрицу корреляции только определенные переменные, вы можете использовать оператор VAR :
/*create correlation matrix using only var1, var2 and var3 in my_data*/
proc corr data =my_data;
var var1, var2, var3;
run ;
В следующем примере показано, как создать корреляционную матрицу в SAS.
Пример. Создание корреляционной матрицы в SAS
Предположим, у нас есть следующий набор данных в SAS, содержащий информацию о различных баскетболистах:
/*create dataset*/
data my_data;
input team $ assists rebounds points;
datalines ;
A 4 12 22
A 5 14 24
A 5 13 26
A 6 7 26
B 7 8 29
B 8 8 32
B 8 9 20
B 10 13 14
;
run ;
/*view dataset*/
proc print data =my_data;
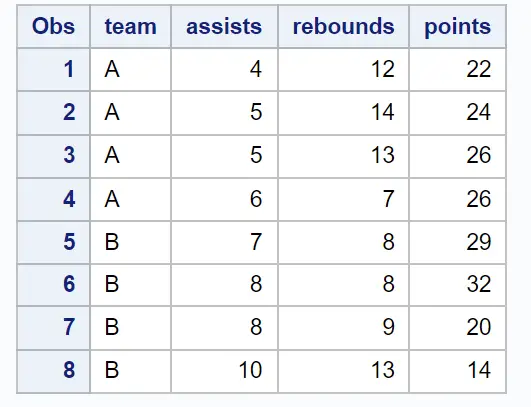
Мы можем использовать оператор PROC CORR для создания корреляционной матрицы, которая по умолчанию включает каждую числовую переменную в наборе данных:
/*create correlation matrix using all numeric variables in my_data*/
proc corr data =my_data;
run ;
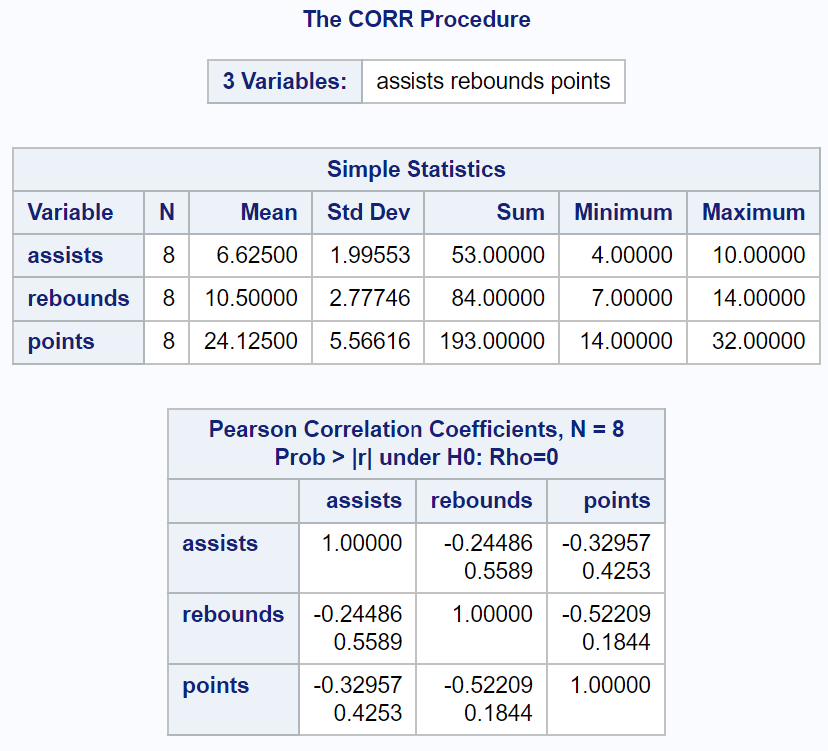
В выходных данных отображается сводная статистика числовых переменных в первой таблице вместе с матрицей корреляции.
Обратите внимание, что переменная «команда» не была включена в корреляционную матрицу, поскольку она не была числовой переменной.
Вот как интерпретировать значения корреляционной матрицы:
(1) Коэффициент корреляции Пирсона (r) между передачами и подборами составляет -0,24486 . Соответствующее значение p составляет 0,5589 .
Поскольку r меньше нуля, это говорит нам о том, что между этими двумя переменными существует отрицательная линейная связь. Однако значение p составляет не менее 0,05, поэтому эта корреляция не является статистически значимой.
(2) Коэффициент корреляции Пирсона (r) между передачами и очками составляет -0,32957 . Соответствующее значение p составляет 0,4253 .
Между этими двумя переменными существует отрицательная линейная связь, но она не является статистически значимой.
(3) Коэффициент корреляции Пирсона (r) между подборами и очками равен -0,52209 . Соответствующее значение p составляет 0,1844 .
Между этими двумя переменными существует отрицательная линейная связь, но она не является статистически значимой.
Обратите внимание, что мы также могли бы использовать оператор VAR , чтобы включить в корреляционную матрицу только определенные числовые переменные:
/*create correlation matrix using only assists and rebounds variables*/
proc corr data =my_data;
var assists rebounds;
run ;

Обратите внимание, что в эту корреляционную матрицу были включены только переменные передач и подборов .
Дополнительные ресурсы
В следующих руководствах объясняется, как выполнять другие распространенные задачи в SAS:
Как создать матрицу диаграммы рассеяния в SAS
Как создавать сводные таблицы в SAS
Как рассчитать коэффициент инфляции дисперсии (VIF) в SAS