Как выполнить корреляционный тест в r (с примерами)

Один из способов количественной оценки взаимосвязи между двумя переменными состоит в использовании коэффициента корреляции Пирсона , который является мерой линейной связи между двумя переменными .

Он всегда принимает значение от -1 до 1, где:

• -1 указывает на совершенно отрицательную линейную корреляцию между двумя переменными.
• 0 указывает на отсутствие линейной корреляции между двумя переменными.
• 1 указывает на совершенно положительную линейную корреляцию между двумя переменными.

Чтобы определить, является ли коэффициент корреляции статистически значимым, вы можете вычислить соответствующие t-показатель и p-значение.

Формула для расчета t-показателя коэффициента корреляции (r):

т = р * √ n-2 / √ 1-r ²

Значение p рассчитывается как соответствующее двустороннее значение p для t-распределения с n-2 степенями свободы.

Пример: корреляционный тест в R

Чтобы определить, является ли коэффициент корреляции между двумя переменными статистически значимым, вы можете выполнить тест корреляции в R, используя следующий синтаксис:

cor.test(x, y, метод=c(«Пирсон», «Кендалл», «Спирмен»))

Золото:

• x, y: векторы цифровых данных.
• метод: метод, используемый для расчета корреляции между двумя векторами. По умолчанию используется «Пирсон».

Например, предположим, что у нас есть следующие два вектора в R:

 x <- c(2, 3, 3, 5, 6, 9, 14, 15, 19, 21, 22, 23)
y <- c(23, 24, 24, 23, 17, 28, 38, 34, 35, 39, 41, 43)

Прежде чем выполнять тест корреляции между двумя переменными, мы можем создать быструю диаграмму рассеяния, чтобы визуализировать их взаимосвязь:

 #create scatterplot
plot(x, y, pch= 16 )

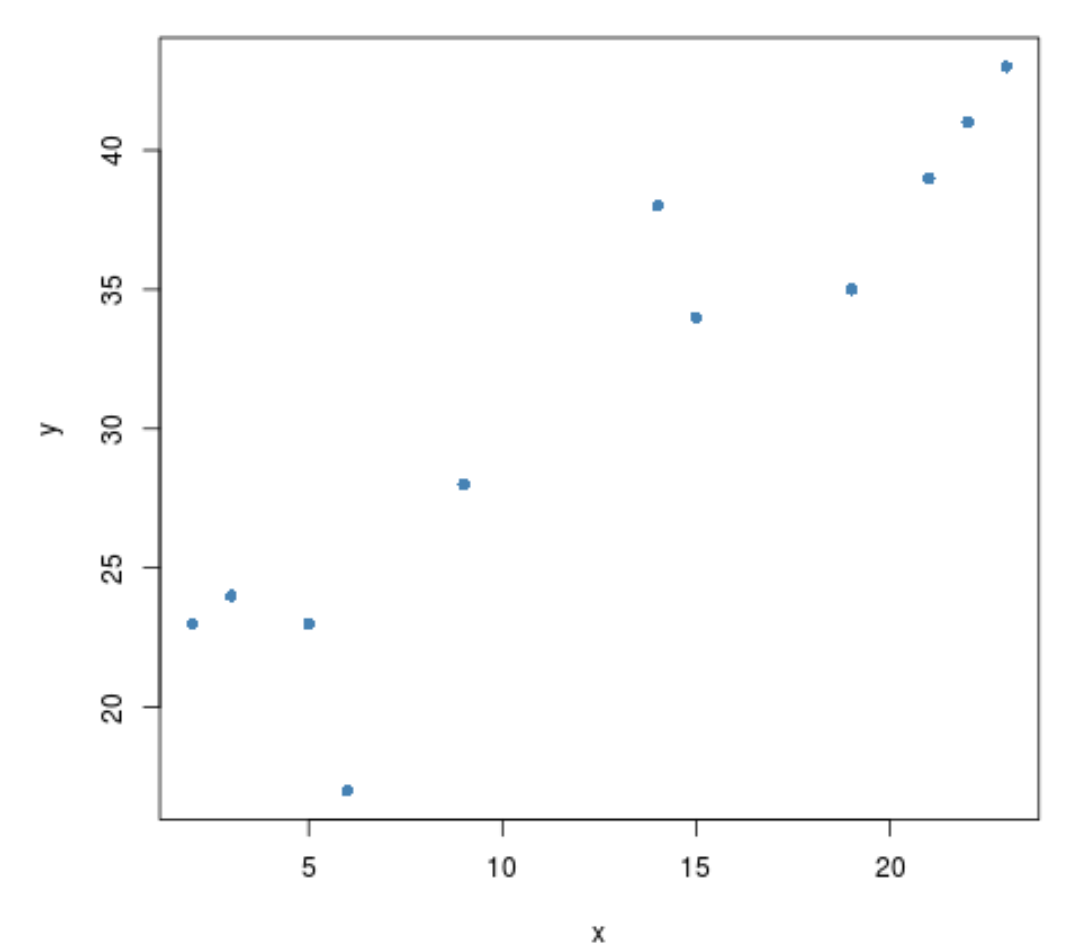
Судя по всему, между этими двумя переменными существует положительная корреляция. То есть, по мере увеличения одного, другое имеет тенденцию к увеличению.

Чтобы увидеть, является ли эта корреляция статистически значимой, мы можем выполнить корреляционный тест:

 #perform correlation test between the two vectors
cor.test(x, y)

	Pearson's product-moment correlation

data: x and y
t = 7.8756, df = 10, p-value = 1.35e-05
alternative hypothesis: true correlation is not equal to 0
95 percent confidence interval:
 0.7575203 0.9799783
sample estimates:
      horn 
0.9279869

Коэффициент корреляции между двумя векторами оказывается равным 0,9279869 .

Статистика теста равна 7,8756 , а соответствующее значение p — 1,35e-05 .

Поскольку это значение меньше 0,05, у нас есть достаточно доказательств, чтобы сказать, что корреляция между двумя переменными статистически значима.

Дополнительные ресурсы

Следующие учебные пособия предоставляют дополнительную информацию о коэффициентах корреляции:

Введение в коэффициент корреляции Пирсона
Что считается «сильной» корреляцией?
Пять гипотез корреляции Пирсона