Как рассчитать корреляцию между непрерывными и категориальными переменными

Когда мы хотим рассчитать корреляцию между двумя непрерывными переменными, мы обычно используем коэффициент корреляции Пирсона .

Однако, когда мы хотим вычислить корреляцию между непрерывной переменной и категориальной переменной , мы можем использовать так называемую точечную бисериальную корреляцию .

Точечная бисериальная корреляция используется для расчета корреляции между бинарной категориальной переменной (переменной, которая может принимать только два значения) и непрерывной переменной и имеет следующие свойства:

• Корреляция между точками и бисериалами может варьироваться от -1 до 1.
• Для каждой группы, созданной бинарной переменной, предполагается, что непрерывная переменная обычно распределяется с равными дисперсиями.
• Для каждой группы, созданной бинарной переменной, предполагается отсутствие экстремальных выбросов.

В следующем примере показано, как на практике вычислить корреляцию между точками и бирядами.

Пример: расчет точечно-бирядной корреляции

Предположим, профессор университета хочет определить, существует ли корреляция между полом и баллом на конкретном квалификационном экзамене.

Он собирает следующие данные о 12 мальчиках и 12 девочках в своем классе:

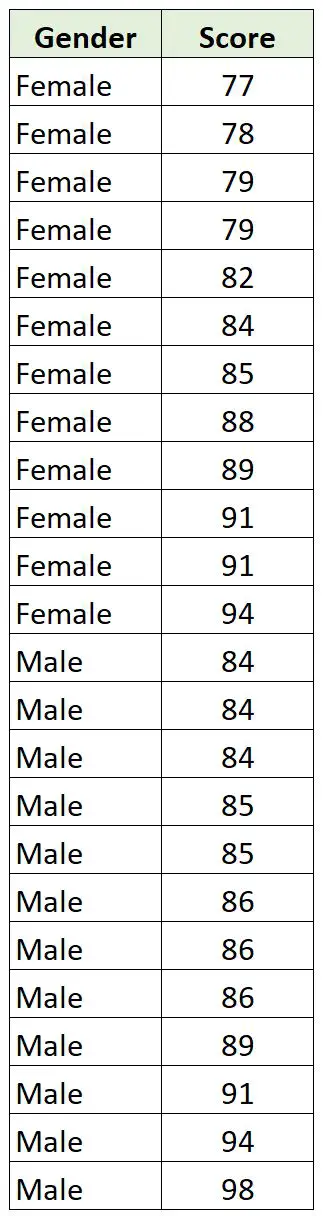
Поскольку пол является категориальной переменной, а балл — непрерывной переменной, имеет смысл вычислить точечную бисериальную корреляцию между двумя переменными.

Профессор может использовать любое статистическое программное обеспечение (включая Excel, R, Python, SPSS, Stata) для расчета точечно-бисериальной корреляции между двумя переменными.

Следующий код показывает, как вычислить корреляцию между точками и бисериалами в R, используя значение 0 для обозначения женщин и 1 для представления мужчин для гендерной переменной:

 #define values for gender
gender <- c(0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0,
            1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1)

#define values for score
score <- c(77, 78, 79, 79, 82, 84, 85, 88, 89, 91, 91, 94,
           84, 84, 84, 85, 85, 86, 86, 86, 89, 91, 94, 98)

#calculate point-biserial correlation
horn. test (gender, score)

	Pearson's product-moment correlation

data: gender and score
t = 1.3739, df = 22, p-value = 0.1833
alternative hypothesis: true correlation is not equal to 0
95 percent confidence interval:
 -0.1379386 0.6147832
sample estimates:
      horn 
0.2810996

Из результата мы видим, что коэффициент точечной бисерийной корреляции равен 0,281 , а соответствующее значение p — 0,1833 .

Поскольку коэффициент корреляции положительный, это говорит нам о наличии положительной корреляции между полом и баллом.

Поскольку мы закодировали мужчин как 1, а женщин как 0, это указывает на то, что баллы, как правило, выше у мужчин (т. е. баллы имеют тенденцию увеличиваться по мере «увеличения» пола). » от 0 до 1).

Однако, поскольку значение p составляет не менее 0,05, этот коэффициент корреляции не является статистически значимым.

Дополнительные ресурсы

В следующих руководствах объясняется, как рассчитать двухрядную корреляцию точек с использованием различного статистического программного обеспечения:

Как рассчитать корреляцию между точками и бирядами в Excel
Как рассчитать двухрядную корреляцию точек в R
Как рассчитать корреляцию между точками и бисериалами в Python