Что такое корреляция нулевого порядка?
В статистике корреляция между двумя переменными говорит нам о взаимосвязи между этими двумя переменными.
Один из самых основных типов корреляции известен как корреляция нулевого порядка , которая относится к корреляции между двумя переменными без учета возможного влияния других переменных.
Примером такого типа корреляции является коэффициент корреляции Пирсона , который измеряет линейную связь между двумя переменными и может принимать значения от -1 до 1, где:
- -1 указывает на совершенно отрицательную линейную корреляцию между двумя переменными.
- 0 указывает на отсутствие линейной корреляции между двумя переменными.
- 1 указывает на совершенно положительную линейную корреляцию между двумя переменными.
Чем дальше корреляция от нуля, тем сильнее связь между двумя переменными.
Корреляции первого и второго порядка
Если мы вычислим корреляцию между двумя переменными A и B, контролируя при этом влияние третьей переменной C, мы бы назвали корреляцию между A и B корреляцией первого порядка .
Аналогично, если мы вычислим корреляцию между двумя переменными A и B, контролируя при этом влияние переменных C и D, мы бы назвали корреляцию между A и B корреляцией второго порядка .
Пример корреляции нулевого порядка
Допустим, у нас есть следующий набор данных, который показывает количество часов, потраченных на обучение, и оценку, полученную на экзамене 10 разными студентами:
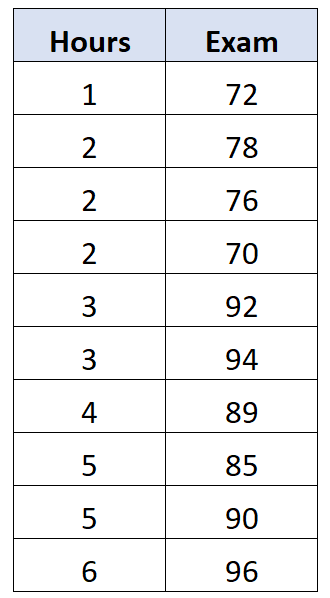
Оказывается, корреляция между этими двумя переменными равна 0,762 . Это будет считаться корреляцией нулевого порядка между двумя переменными, поскольку мы не контролируем потенциальное влияние третьей переменной.
Однако в действительности возможно, что на взаимосвязь между этими двумя переменными влияют и другие факторы.
Например, текущая оценка учащегося в классе может повлиять на его оценку на экзамене. Предположим, у нас также есть доступ к этим данным:
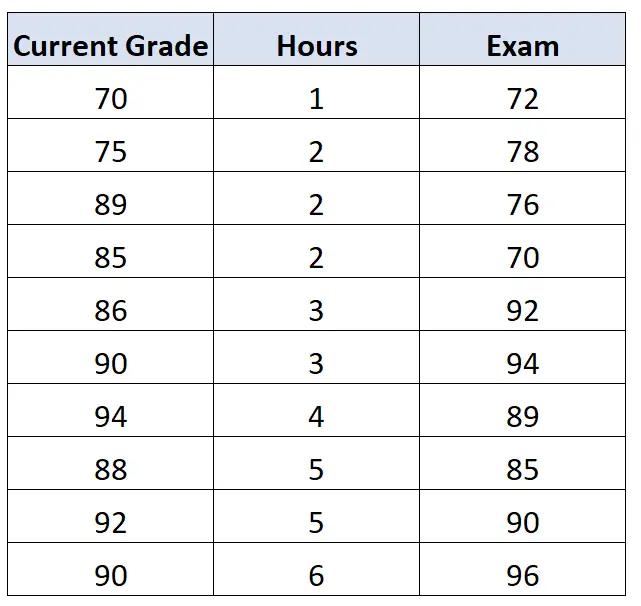
Если бы мы затем рассчитали корреляцию между часами и экзаменом , учитывая при этом влияние текущей оценки , мы бы обнаружили, что корреляция первого порядка между часами и экзаменом равна 0,578 .
Это означает, что по-прежнему существует довольно сильная положительная корреляция между учебными часами и оценкой на экзамене, даже после учета влияния текущей оценки учащегося в классе.
Примечание. Корреляцию первого порядка иногда называют частичной корреляцией . В этом руководстве объясняется, как рассчитать частичные корреляции в Excel.
Корреляции нулевого порядка в корреляционной матрице
мы создаем матрицу корреляции. Всякий раз, когда для набора переменных коэффициенты корреляции, отображаемые в матрице, всегда представляют собой корреляции нулевого порядка, поскольку они представляют собой просто корреляции между каждой парной комбинацией переменных без учета влияния других переменных.
Например, рассмотрим наш набор данных из предыдущего примера:

Если бы мы создали корреляционную матрицу для этого набора данных, она выглядела бы так:
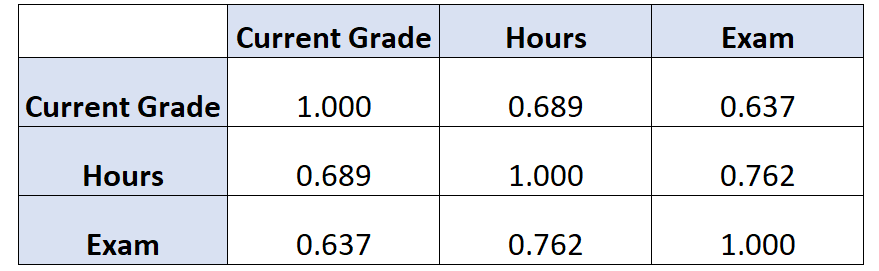
Способ интерпретации:
- Корреляция между текущей оценкой и количеством изученных часов составляет 0,689 .
- Корреляция между текущим баллом и баллом, полученным на экзамене, составляет 0,637 .
- Корреляция между учебными часами и баллами на экзамене составляет 0,762 .
Каждая из этих корреляций является корреляцией нулевого порядка .
Дополнительные ресурсы
Следующие учебные пособия предоставляют дополнительную информацию о коэффициентах корреляции:
Введение в коэффициент корреляции Пирсона
Как читать корреляционную матрицу
Как рассчитать частичную корреляцию в Excel