Корреляция против. ассоциация: в чем разница?
Два термина, которые иногда используются как взаимозаменяемые, — это корреляция и ассоциация . Однако в области статистики эти два термина имеют несколько разное значение.
В частности, когда мы используем слово корреляция , мы обычно говорим о коэффициенте корреляции Пирсона . Это мера линейной связи между двумя случайными величинами X и Y. Она имеет значение от -1 до 1, где:
- -1 указывает на совершенно отрицательную линейную корреляцию между двумя переменными.
- 0 указывает на отсутствие линейной корреляции между двумя переменными.
- 1 указывает на совершенно положительную линейную корреляцию между двумя переменными.
И наоборот, когда статистики используют слово « ассоциация» , они могут иметь в виду любую связь между двумя переменными, будь то линейную или нелинейную.
Чтобы проиллюстрировать эту идею, рассмотрим следующие примеры.
Визуализация корреляции и связи с облаками точек
Мы используем два слова для описания корреляции между двумя случайными величинами:
1 направление
- Положительный: две случайные величины имеют положительную корреляцию, если Y имеет тенденцию увеличиваться по мере увеличения X.
- Отрицательный: две случайные величины имеют отрицательную корреляцию, если Y имеет тенденцию уменьшаться по мере увеличения X.
2. Сила
- Низкая: две случайные величины имеют низкую корреляцию, если точки на диаграмме рассеяния разбросаны редко.
- Сильная: две случайные величины имеют сильную корреляцию, если точки на диаграмме рассеяния тесно сгруппированы вместе.
Следующие диаграммы рассеяния иллюстрируют примеры каждого типа корреляции:
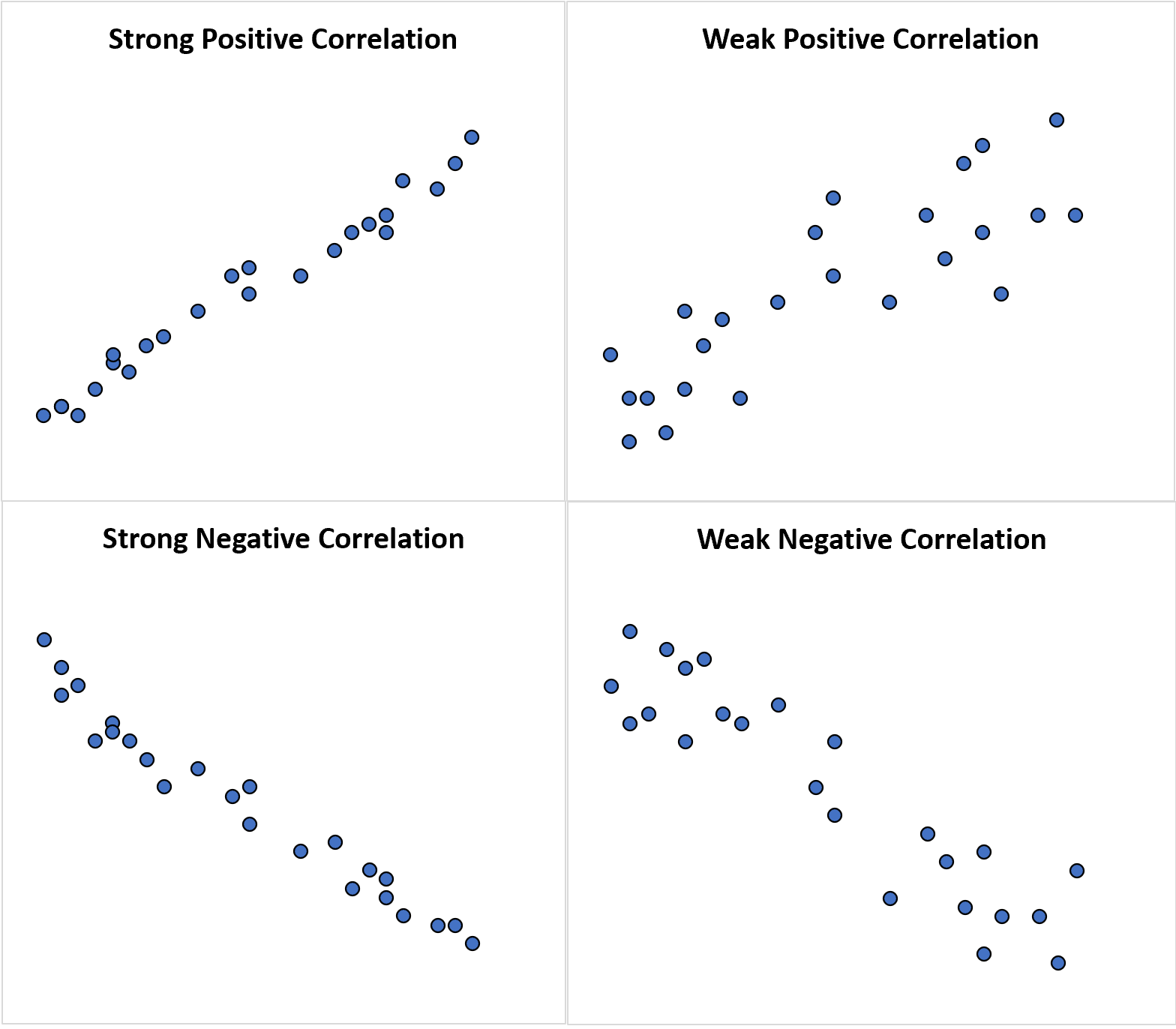
По сравнению с корреляцией, словесная ассоциация может сказать нам, существует ли связь между двумя случайными величинами: линейная или нелинейная.
Следующие диаграммы рассеяния иллюстрируют некоторые примеры:
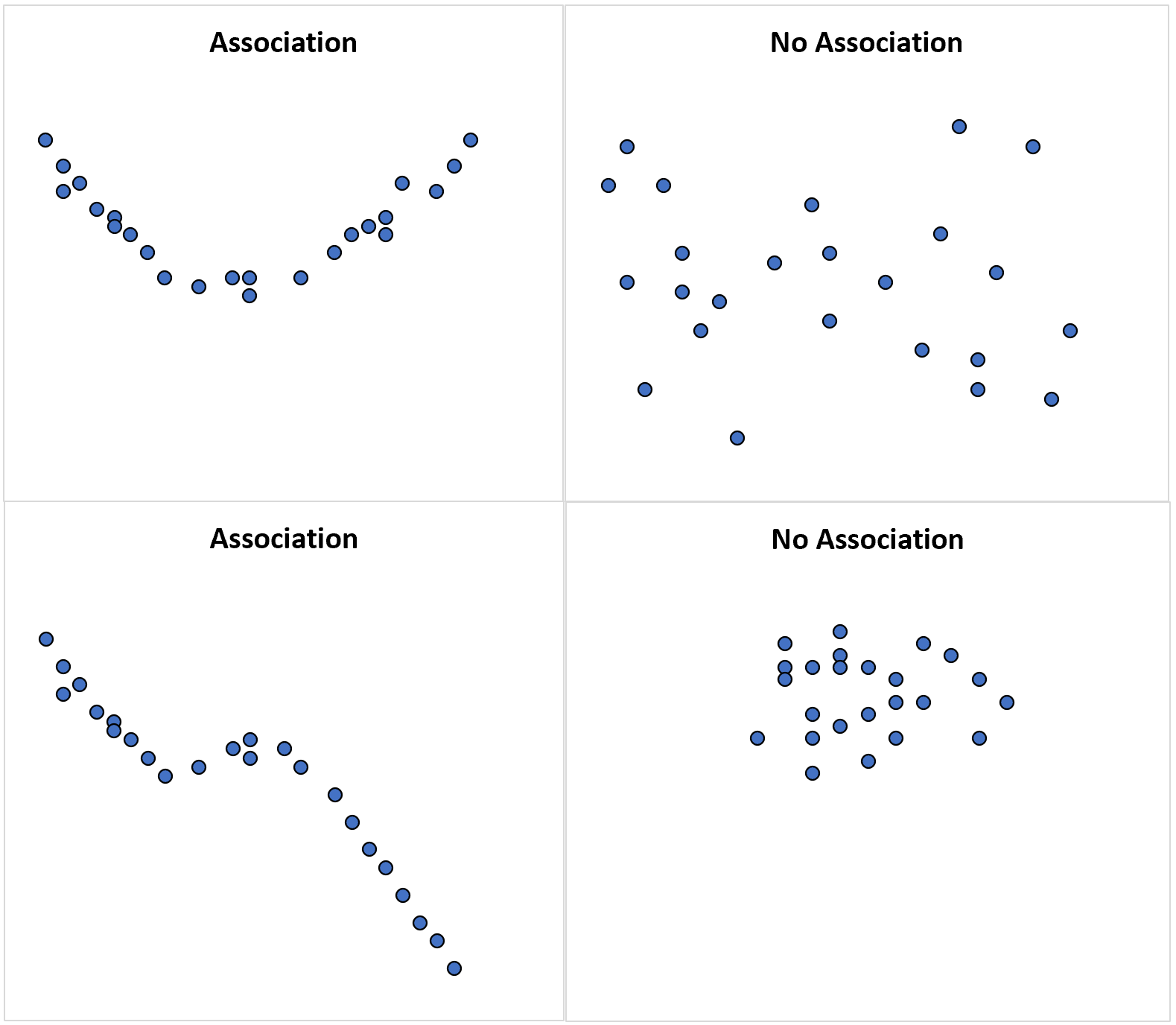
Диаграмма рассеяния в верхнем левом углу иллюстрирует квадратичную зависимость между двумя случайными величинами, что означает, что связь между двумя переменными существует , но она не является линейной.
Если бы мы вычислили корреляцию между двумя переменными, она, вероятно, была бы близка к нулю, поскольку между ними нет линейной зависимости.
Однако простое знание того, что корреляция между двумя переменными равна нулю, может ввести в заблуждение, поскольку скрывает тот факт, что вместо этого существует нелинейная связь.
Корреляция против. ассоциация: резюме
Термины корреляция и ассоциация имеют следующие сходства и различия:
Сходства:
- Оба термина используются для описания того, существует ли связь между двумя случайными величинами.
- Оба термина могут использовать диаграммы рассеяния для анализа взаимосвязи между двумя случайными величинами.
Отличия:
- Корреляция может только сказать нам, имеют ли две случайные величины линейную связь, тогда как ассоциация может сказать нам, имеют ли две случайные величины линейную или нелинейную связь.
- Корреляция количественно определяет связь между двумя случайными величинами, используя число от -1 до 1, но ассоциация не использует конкретное число для количественной оценки связи.
Дополнительные ресурсы
Введение в коэффициент корреляции Пирсона
Введение в облака точек
Корреляция и регрессия: в чем разница?