Корреляция и регрессия: в чем разница?
Корреляция и регрессия — два связанных, но не совсем одинаковых статистических термина.
В этом уроке мы дадим краткое объяснение обоих терминов и объясним, чем они похожи и отличаются.
Что такое корреляция?
Корреляция измеряет линейную связь между двумя переменными, x и y . Он имеет значение от -1 до 1, где:
- -1 указывает на совершенно отрицательную линейную корреляцию между двумя переменными.
- 0 указывает на отсутствие линейной корреляции между двумя переменными.
- 1 указывает на совершенно положительную линейную корреляцию между двумя переменными.
Например, предположим, что у нас есть следующий набор данных, который содержит две переменные: (1) количество учебных часов и (2) баллы на экзаменах, полученные для 20 разных студентов:

Если бы мы создали диаграмму количества учебных часов и результатов экзаменов, она бы выглядела следующим образом:
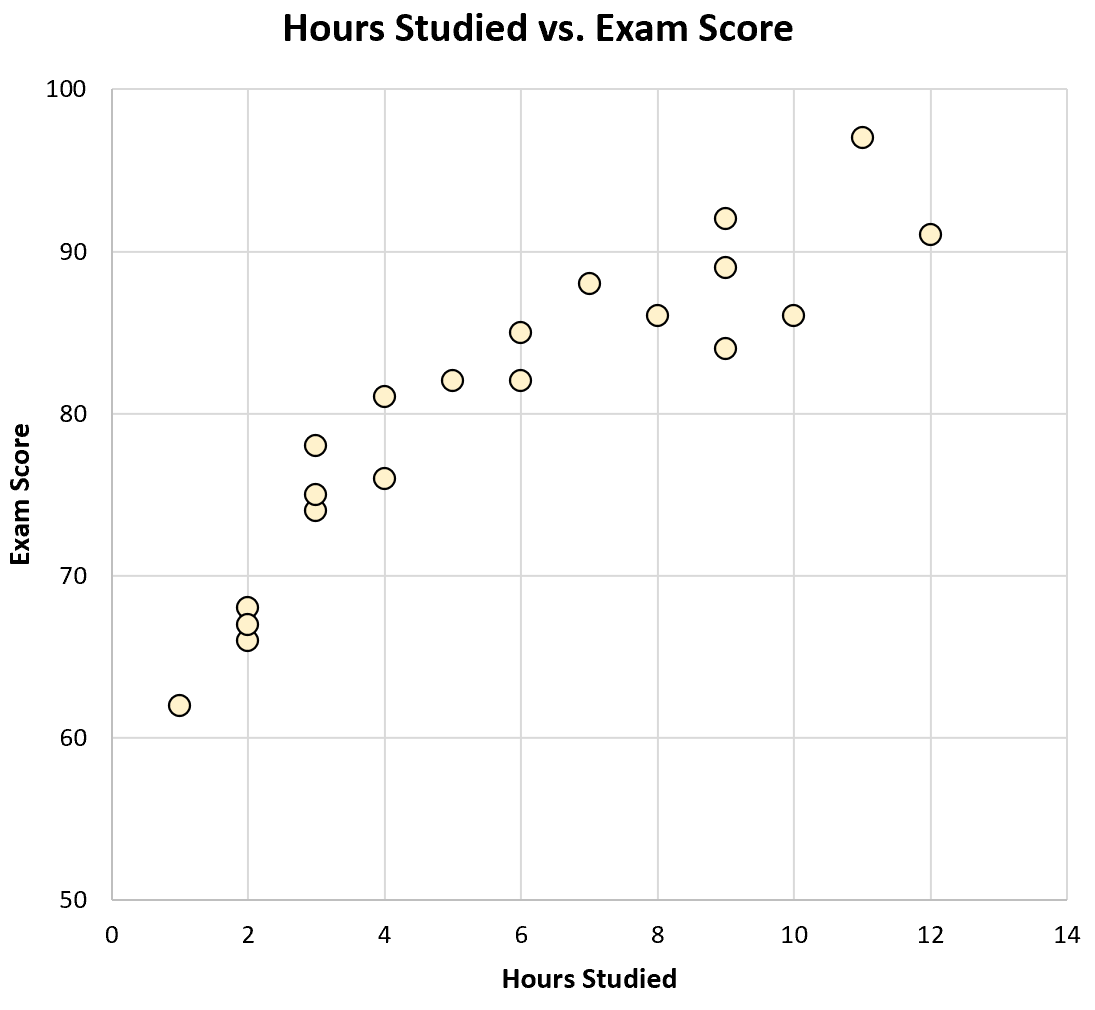
Просто взглянув на график, мы видим, что студенты, которые больше учатся, как правило, лучше сдают экзамены. Другими словами, мы можем визуально видеть, что между двумя переменными существует положительная корреляция .
Используя калькулятор, мы видим, что корреляция между этими двумя переменными равна r = 0,915 . Поскольку это значение близко к 1, оно подтверждает наличие сильной положительной корреляции между двумя переменными.
Что такое регрессия?
Регрессия — это метод, который мы можем использовать, чтобы понять, как изменение значений переменной x влияет на значения переменной y .
Модель регрессии использует одну переменную x в качестве переменной-предиктора, а другую переменную y в качестве переменной отклика . Затем он находит уравнение следующей формы, которое лучше всего описывает связь между двумя переменными:
ŷ = б 0 + б 1 х
Золото:
- ŷ: прогнозируемое значение переменной ответа.
- b 0 : Ордината в начале координат (значение y, когда x равно нулю)
- b 1 : Коэффициент регрессии (среднее увеличение y при увеличении x на одну единицу)
- x: значение прогнозируемой переменной
Например, рассмотрим наш предыдущий набор данных:

Используя калькулятор линейной регрессии , мы обнаруживаем, что следующее уравнение лучше всего описывает взаимосвязь между этими двумя переменными:
Прогнозируемый результат экзамена = 65,47 + 2,58*(учебные часы)
Способ интерпретации этого уравнения:
- Прогнозируемый результат экзамена для студента, обучающегося ноль часов, составляет 65,47 .
- Средний прирост балла на экзамене, связанный с дополнительным часом обучения, составляет 2,58 .
Мы также можем использовать это уравнение, чтобы спрогнозировать оценку, которую получит студент, исходя из количества изученных часов.
Например, студент, который учится 6 часов, должен получить оценку 80,95 :
Прогнозируемая оценка экзамена = 65,47 + 2,58*(6) = 80,95 .
Мы также можем построить это уравнение в виде линии на диаграмме рассеяния:
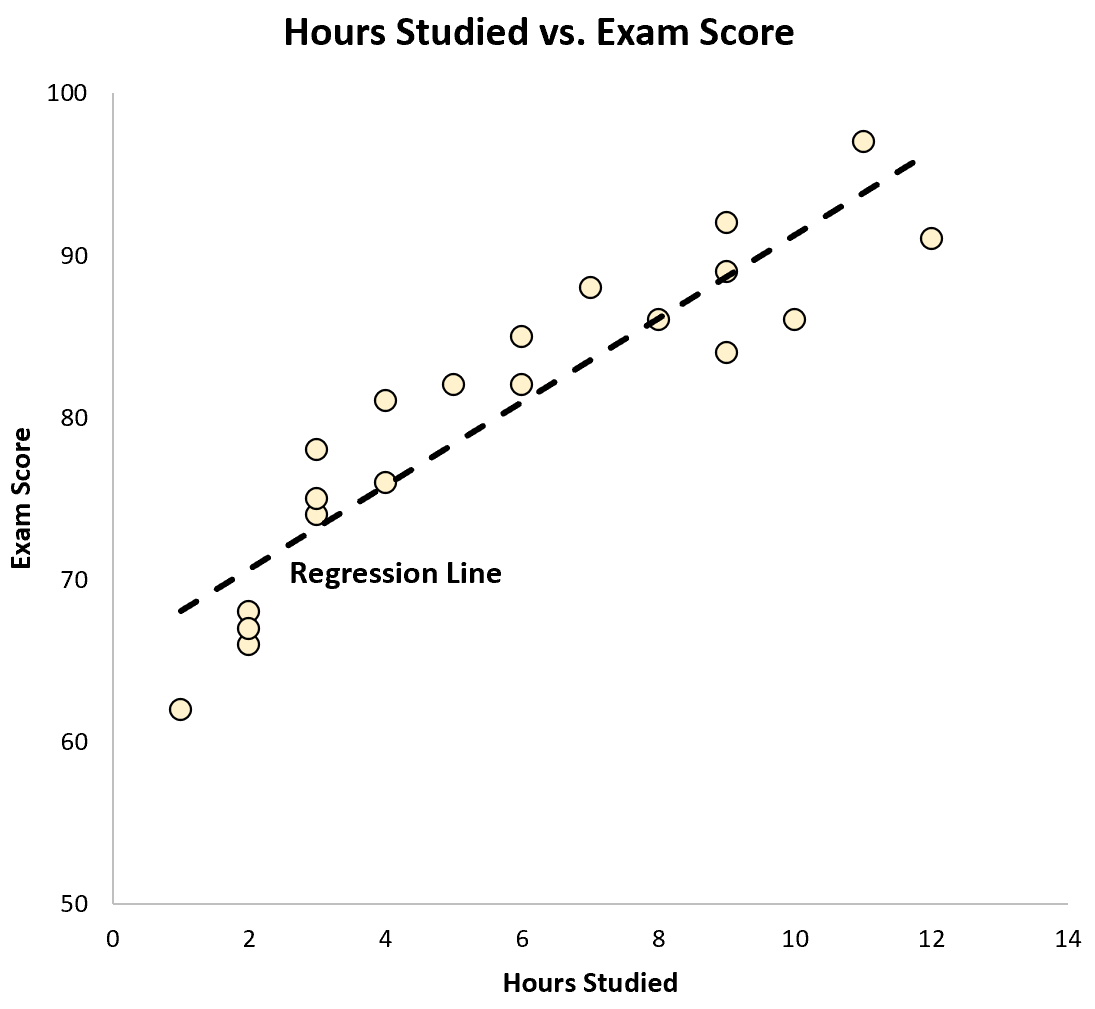
Мы видим, что линия регрессии достаточно хорошо «соответствует» данным.
Напомним, ранее корреляция между этими двумя переменными составляла r = 0,915 . Оказывается, мы можем возвести это значение в квадрат и получить число под названием «r в квадрате», которое описывает общую долю дисперсии переменной ответа, которую можно объяснить переменной-предиктором.
В этом примере r 2 = 0,915 2 = 0,837 . Это означает, что 83,7% различий в результатах экзаменов можно объяснить количеством изученных часов.
Корреляция против регрессии: сходства и различия
Вот краткое изложение сходств и различий между корреляцией и регрессией:
Сходства:
- Оба количественно определяют направление связи между двумя переменными.
- Оба количественно определяют силу связи между двумя переменными.
Отличия:
- Регрессия способна показать причинно-следственную связь между двумя переменными. Корреляция этого не делает.
- Регрессия позволяет использовать уравнение для прогнозирования значения одной переменной на основе значения другой переменной. Корреляция этого не делает.
- Регрессия использует уравнение для количественной оценки связи между двумя переменными. Корреляция использует одно число.
Дополнительные ресурсы
Следующие руководства предлагают более глубокие объяснения тем, затронутых в этой статье.
Введение в коэффициент корреляции Пирсона
Введение в простую линейную регрессию
Простой калькулятор линейной регрессии
Что такое хорошее значение R-квадрата?