Коэффициент асимметрии пирсона в excel (шаг за шагом)

Коэффициент асимметрии Пирсона , разработанный биостатистиком Карлом Пирсоном , представляет собой способ измерения асимметрии выборочного набора данных.

На самом деле существует два метода, которые можно использовать для расчета коэффициента асимметрии Пирсона:

Способ 1: использовать режим

Асимметрия = (Среднее значение – Режим) / Стандартное отклонение выборки

Метод 2: использование медианы

Асимметрия = 3 (Среднее – Медиана) / Стандартное отклонение выборки

В общем, второй метод предпочтителен, поскольку режим не всегда является хорошим показателем того, где находится «центральное» значение набора данных, и в заданном наборе данных может быть более одного режима.

В следующем пошаговом примере показано, как рассчитать обе версии коэффициента асимметрии Пирсона для заданного набора данных в Excel.

Шаг 1. Создайте набор данных

Сначала давайте создадим следующий набор данных в Excel:

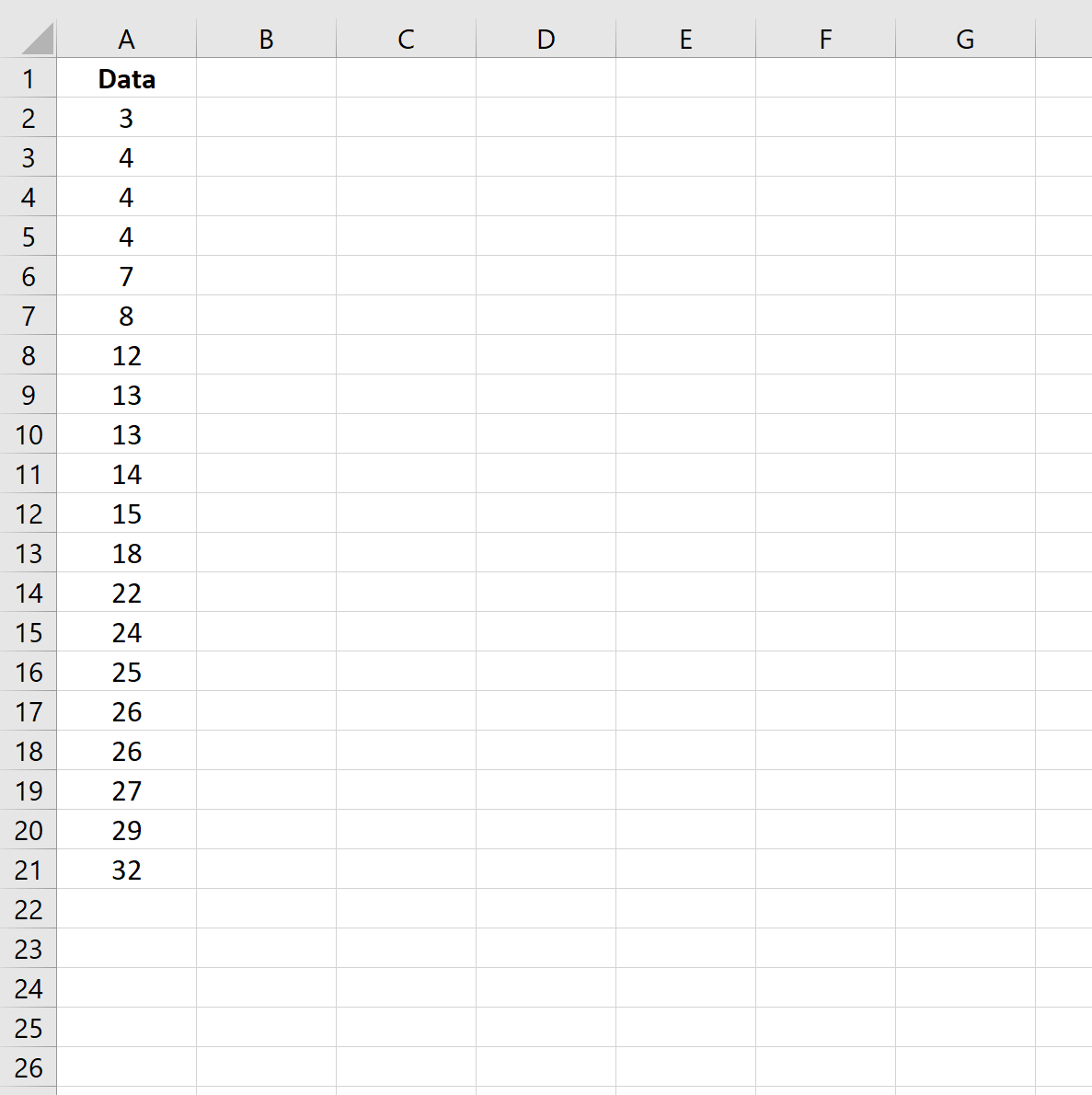
Шаг 2. Рассчитайте коэффициент асимметрии Пирсона (с использованием режима)

Затем мы можем использовать следующую формулу для расчета коэффициента асимметрии Пирсона с использованием режима:

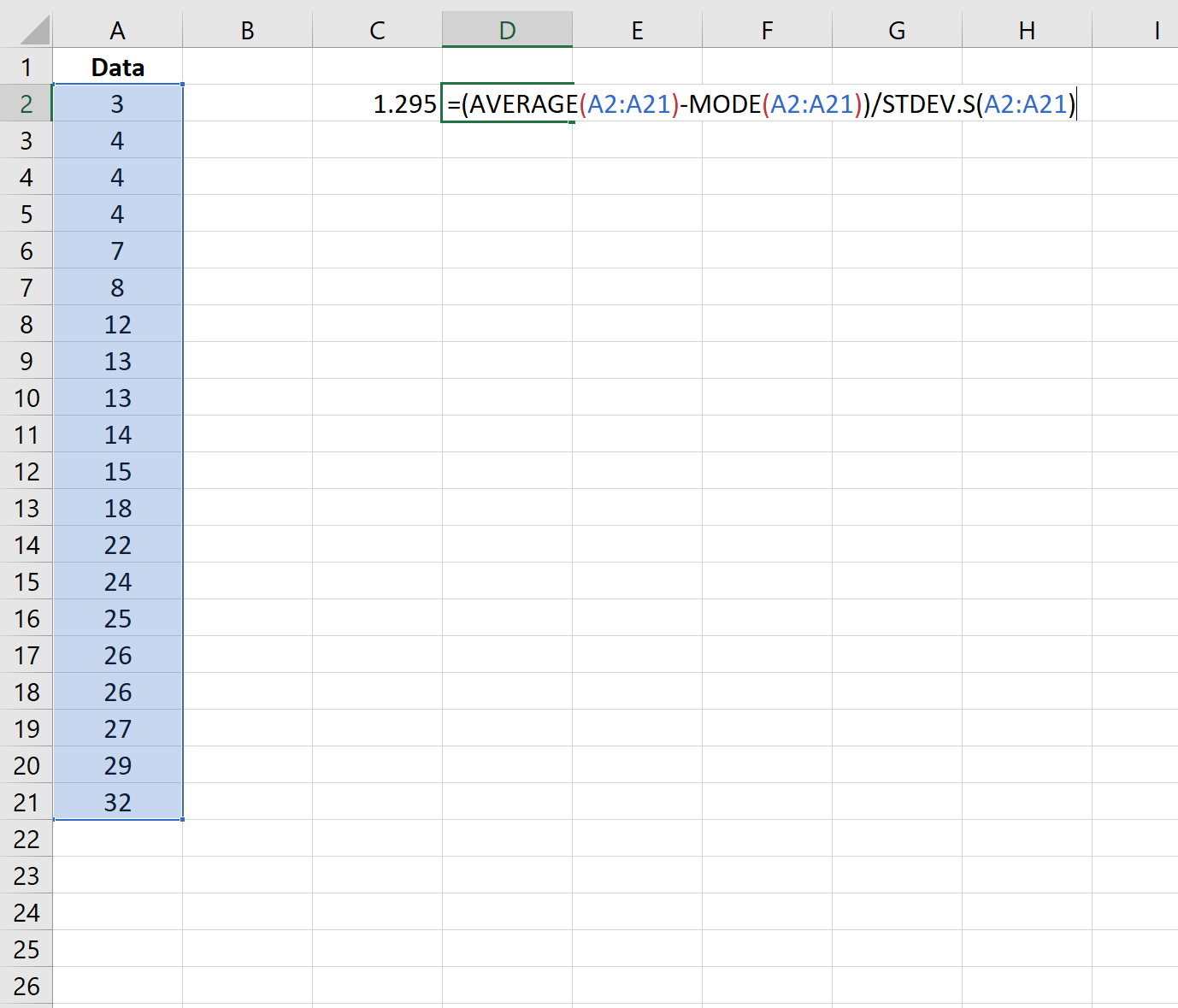
Асимметрия оказывается равной 1,295 .

Шаг 3. Рассчитайте коэффициент асимметрии Пирсона (используя медиану)

Мы также можем использовать следующую формулу для расчета коэффициента асимметрии Пирсона с использованием медианы:

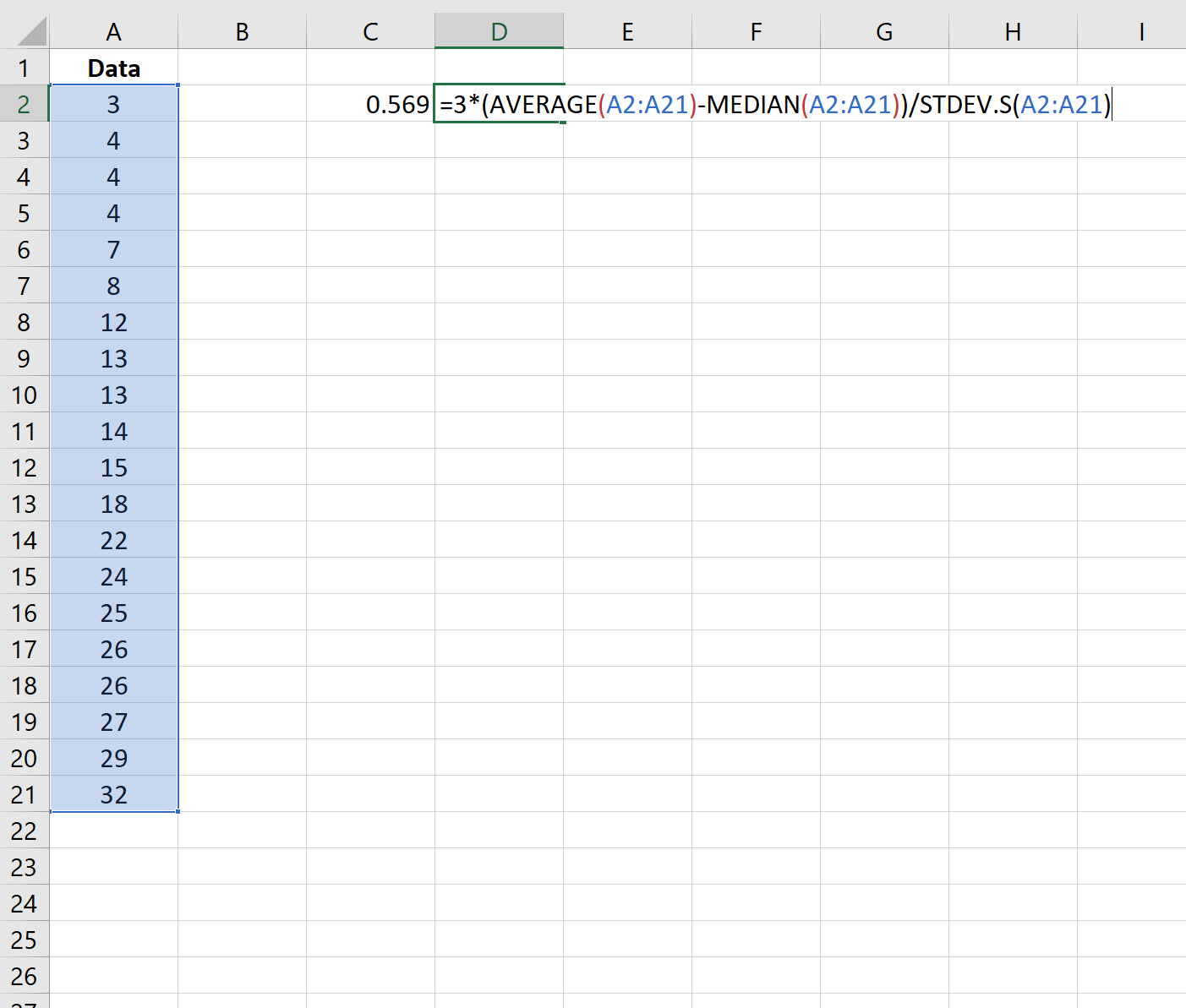
Асимметрия оказывается равной 0,569 .

Как интерпретировать асимметрию

Мы интерпретируем коэффициент асимметрии Пирсона следующим образом:

• Значение 0 указывает на отсутствие асимметрии. Если бы мы создали гистограмму для визуализации распределения значений в наборе данных, она была бы совершенно симметричной.
• Положительное значение указывает на положительный наклон или наклон «вправо». Гистограмма покажет «хвост» на правой стороне распределения.
• Отрицательное значение указывает на отрицательный наклон или наклон «влево». Гистограмма покажет «хвост» на левой стороне распределения.

В нашем предыдущем примере асимметрия была положительной, что указывает на то, что распределение значений данных было положительно асимметричным или «правильным».

Дополнительные ресурсы

Прочтите эту статью , чтобы получить хорошее объяснение асимметричного распределения влево и вправо.