Коэффициент корреляции пирсона

К бенджамин андерсон 5 августа, 2023 Статистика 0 комментариев

В этой статье объясняется, что такое коэффициент корреляции Пирсона (или коэффициент линейной корреляции) и для чего он используется. Вы узнаете, как рассчитать коэффициент корреляции Пирсона, выполнив пошаговое упражнение. Кроме того, вы можете найти значение коэффициента корреляции Пирсона для любого набора данных с помощью онлайн-калькулятора в конце.

Что такое коэффициент корреляции Пирсона?

Коэффициент корреляции Пирсона , также называемый коэффициентом линейной корреляции или просто коэффициентом корреляции , представляет собой статистическую меру, которая указывает на взаимосвязь между двумя переменными.

Чтобы рассчитать коэффициент корреляции Пирсона между двумя переменными, необходимо разделить ковариацию указанных переменных на квадратный корень из произведения их дисперсий.

Таким образом, коэффициент корреляции Пирсона пытается количественно оценить линейную зависимость между двумя количественными случайными величинами. Априори, численная оценка корреляции между переменными сложна, поскольку трудно определить, что пара переменных более коррелирует между собой, если, как в случае с pues, цель коэффициента корреляции Пирсона состоит в том, чтобы оценить связь между переменными, чтобы иметь возможность сравните между ними.

Значение индекса корреляции Пирсона находится в пределах от -1 до +1 включительно. Ниже мы увидим, как интерпретируется значение коэффициента корреляции Пирсона.

Формула коэффициента корреляции Пирсона

Коэффициент корреляции Пирсона двух статистических переменных равен частному между ковариацией переменных и квадратным корнем из произведения дисперсии каждой переменной.

Следовательно, формула расчета коэффициента корреляции Пирсона выглядит следующим образом:

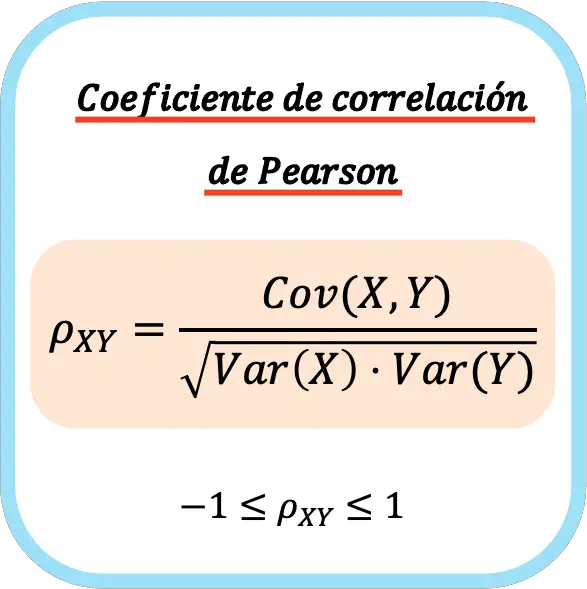
Коэффициент корреляции Пирсона, коэффициент линейной корреляции

👉 Вы можете использовать калькулятор ниже, чтобы рассчитать коэффициент корреляции Пирсона для любого набора данных.

Когда коэффициент корреляции Пирсона рассчитывается для популяции, он обычно обозначается греческой буквой ρ. Но когда коэффициент рассчитывается относительно выборки, в качестве обозначения обычно используется буква r.

Имейте в виду, что для определения коэффициента корреляции Пирсона важно знать, как рассчитать ковариацию между двумя переменными и дисперсию переменной. Кроме того, вам необходимо понимать, что означают эти статистические показатели. Поэтому, прежде чем продолжить объяснение, рекомендуется прочитать следующие две статьи:

➤ См.: как рассчитать ковариацию
➤ См.: как рассчитать зазор

Пример расчета коэффициента корреляции Пирсона

Учитывая определение коэффициента корреляции Пирсона и его формулу, ниже приведен пошаговый пример, чтобы вы могли увидеть, как он рассчитывается.

Рассчитайте коэффициент корреляции Пирсона между следующими двумя непрерывными переменными:

Прежде чем рассчитывать коэффициент корреляции Пирсона, мы представим набор данных на диаграмме рассеяния, чтобы проанализировать взаимосвязь между двумя переменными:

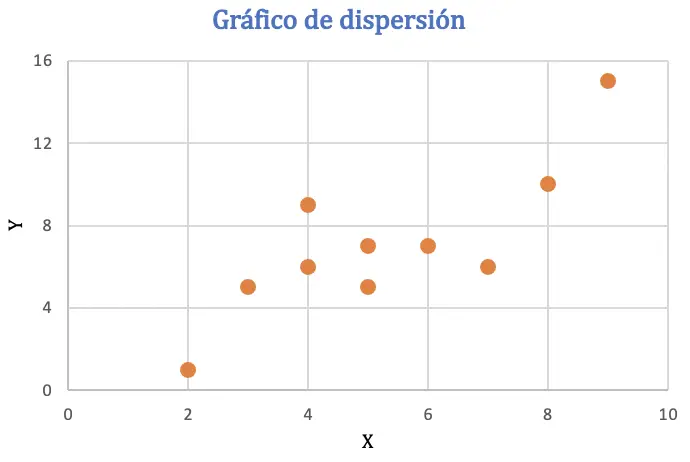
Из диаграммы рассеяния можно сделать вывод, что данные могут иметь положительную тенденцию, или, другими словами, когда значение одной переменной увеличивается, другая переменная также увеличивается. Чтобы проверить корреляцию, найдем коэффициент Пирсона.

Первое, что нужно сделать, — это найти среднее арифметическое каждой переменной в отдельности, что эквивалентно общей сумме данных, деленной на количество наблюдений.

$\overline{x}=\cfrac{\displaystyle \sum_{i=1}^n x_i}{n}=\cfrac{53}{10}=5,3$

$\overline{y}=\cfrac{\displaystyle \sum_{i=1}^n y_i}{n}=\cfrac{71}{10}=7,1$

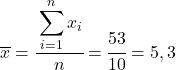
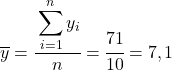
Теперь, когда мы знаем среднее значение каждой переменной, нам нужно добавить в таблицу данных следующие столбцы:

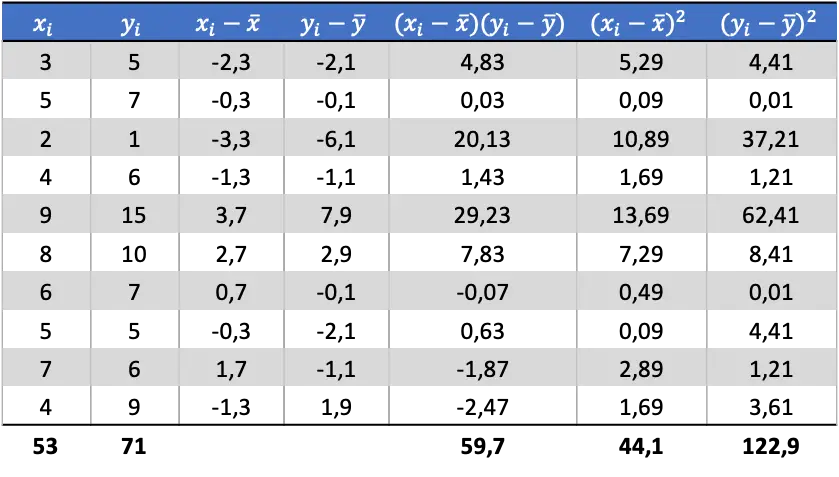
Таблица данных расчета коэффициента Пирсона

По рассчитанным данным таблицы определяем значения ковариации и дисперсии (если вы не помните, как это делалось, выше есть две ссылки, где это подробно описано):

$Cov(X,Y)=\cfrac{\displaystyle \sum_{i=1}^n (x_i-\overline{x})(y_i-\overline{y})}{n}=\cfrac{59,7}{10}=5,97$

$Var(X)=\cfrac{\displaystyle\sum_{i=1}^n\left(x_i-\overline{x}\right)^2}{n}=\cfrac{44,1}{10}=4,41$

$Var(Y)=\cfrac{\displaystyle\sum_{i=1}^n\left(y_i-\overline{y}\right)^2}{n}=\cfrac{122,9}{10}=12,29$

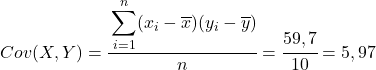
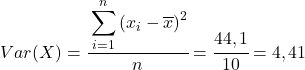
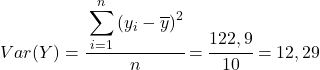
Наконец, просто примените формулу коэффициента корреляции Пирсона, чтобы получить его значение:

$\rho_{XY}=\cfrac{Cov(X,Y)}{\sqrt{Var(X)\cdot Var(Y)}}=\cfrac{5,97}{\sqrt{4,41\cdot 12,29}}=0,81$

Коэффициент корреляции Пирсона имеет значение, очень близкое к 1, что означает, что эти две переменные имеют достаточно сильную положительную корреляцию.

Как вы видели, для определения коэффициента корреляции Пирсона очень полезно использовать такие программы, как Excel, которые позволяют быстрее выполнять вычисления по столбцам.

Калькулятор коэффициента корреляции Пирсона

Введите набор статистических данных в следующий калькулятор, чтобы рассчитать коэффициент корреляции Пирсона между двумя переменными. Вам нужно разделить пары данных так, чтобы в первом поле были только значения одной переменной, а во втором поле — только значения второй переменной.

Данные должны быть разделены пробелом и введены с использованием точки в качестве десятичного разделителя.

Интерпретация коэффициента корреляции Пирсона

В этом разделе мы увидим, как интерпретировать коэффициент корреляции Пирсона, поскольку недостаточно знать его значение, необходимо уметь анализировать его значение.

Таким образом , интерпретация коэффициента корреляции Пирсона зависит от его значения:

r=-1 : две переменные имеют идеальную отрицательную корреляцию, поэтому мы можем нарисовать линию с отрицательным наклоном, в которой все точки соединяются.
-1<r<0 : корреляция между двумя переменными отрицательна, поэтому, когда одна переменная увеличивается, другая уменьшается. Чем ближе значение к -1, тем более отрицательно связаны переменные.
r=0 : корреляция между двумя переменными очень слабая, фактически линейная связь между ними равна нулю. Это не означает, что переменные независимы, поскольку между ними может быть нелинейная связь.
0<r<1 : корреляция между двумя переменными положительна, чем ближе значение к +1, тем сильнее связь между переменными. В этом случае одна переменная имеет тенденцию увеличиваться в значении, когда другая также увеличивается.
r=1 : две переменные имеют идеальную положительную корреляцию, то есть имеют положительную линейную связь.

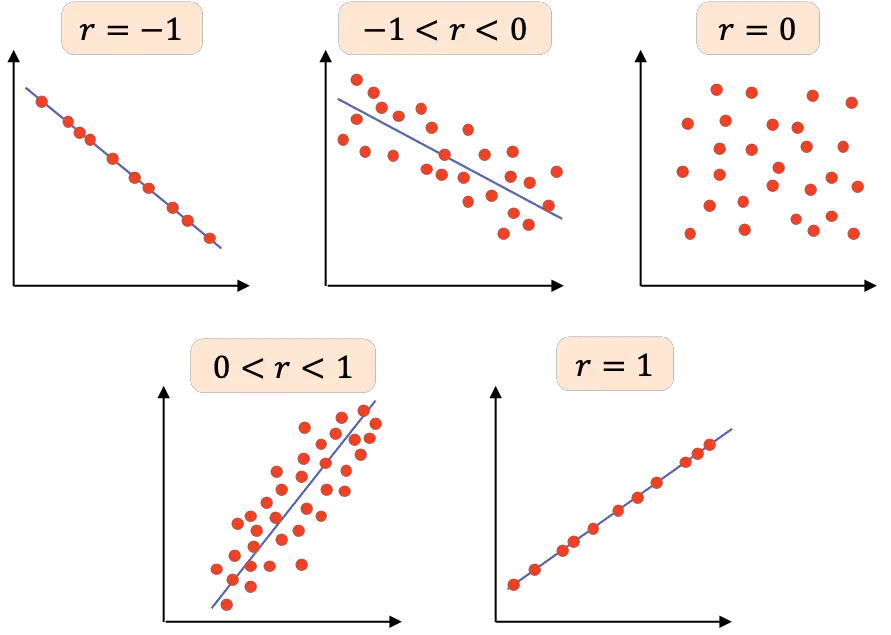
Таким образом, в следующей таблице представлены различные интерпретации коэффициента корреляции Пирсона:

Ценить	Интерпретация
г=-1	Совершенная отрицательная корреляция.
-1<r<0	Отрицательная корреляция: чем ближе корреляция к -1, тем она сильнее.
р=0	Нулевая линейная корреляция.
0<г<1	Положительная корреляция: чем ближе корреляция к +1, тем она сильнее.
р=1	Идеальная положительная корреляция.

Имейте в виду, что даже если между двумя переменными существует связь, это не означает, что между ними существует причинно-следственная связь, т.е. корреляция между двумя переменными не означает, что изменение переменной является причиной изменения переменной. другая переменная.

Например, если мы обнаружим, что существует положительная связь между выработкой двух разных гормонов в организме, не обязательно, что увеличение одного гормона приводит к увеличению другого гормона. Возможно, организм вырабатывает оба гормона, потому что ему нужны оба гормона для борьбы с болезнью, и поэтому уровень обоих гормонов повышается одновременно, и в этом случае причиной будет болезнь. Чтобы определить, существует ли причинно-следственная связь между двумя гормонами, необходимо провести дальнейшее исследование.

Об авторе

бенджамин андерсон

Здравствуйте, я Бенджамин, профессор статистики на пенсии, ставший преданным преподавателем Statorials. Имея обширный опыт и знания в области статистики, я хочу поделиться своими знаниями, чтобы расширить возможности студентов с помощью Statorials. Узнать больше