Что такое криволинейная регрессия? (определение и примеры)
Криволинейная регрессия — это название любой модели регрессии, которая пытается соответствовать кривой , а не прямой линии.
Общие примеры моделей криволинейной регрессии включают:
Квадратичная регрессия: используется, когда существует квадратичная связь между переменной-предиктором и переменной отклика . На графике этот тип отношений выглядит как буква «U» или перевернутая буква «U» на диаграмме рассеяния:
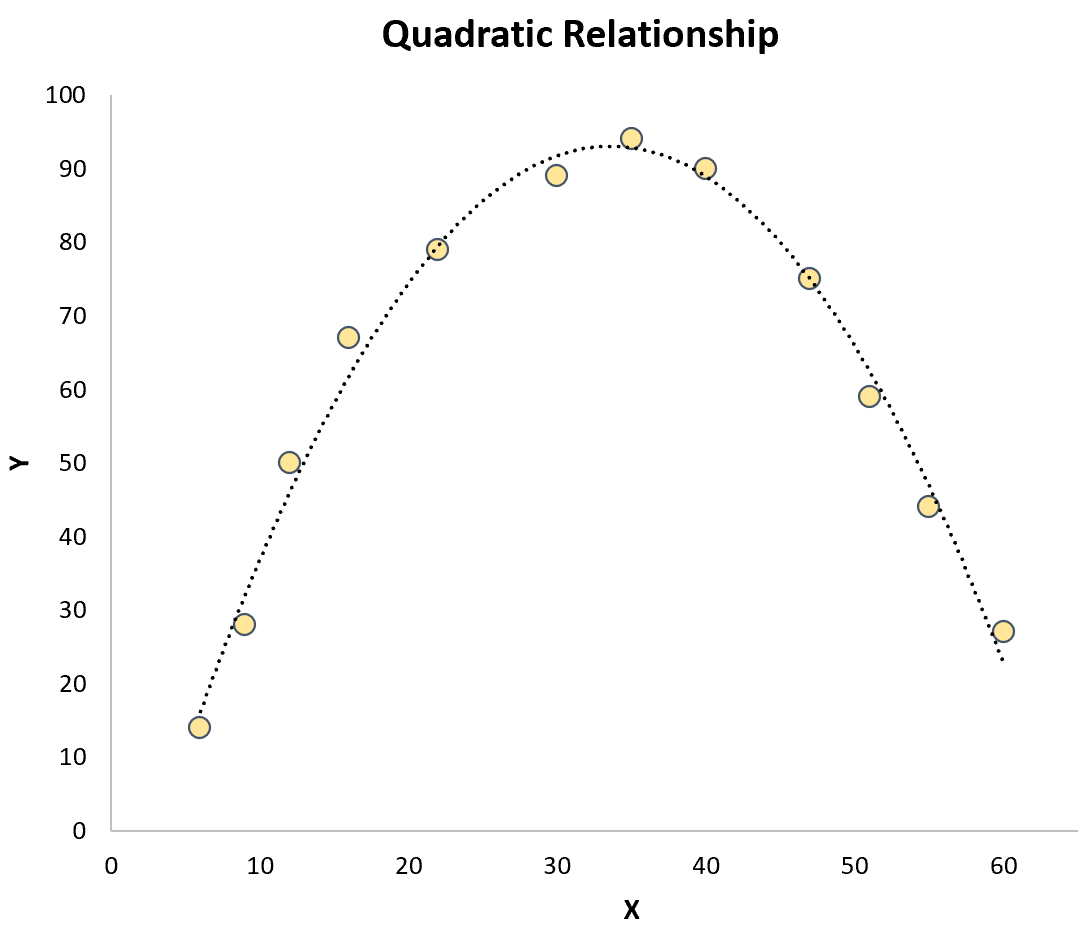
Кубическая регрессия: используется, когда существует кубическая связь между переменной-предиктором и переменной ответа. На графике этот тип отношений показывает две отдельные кривые на диаграмме рассеяния:
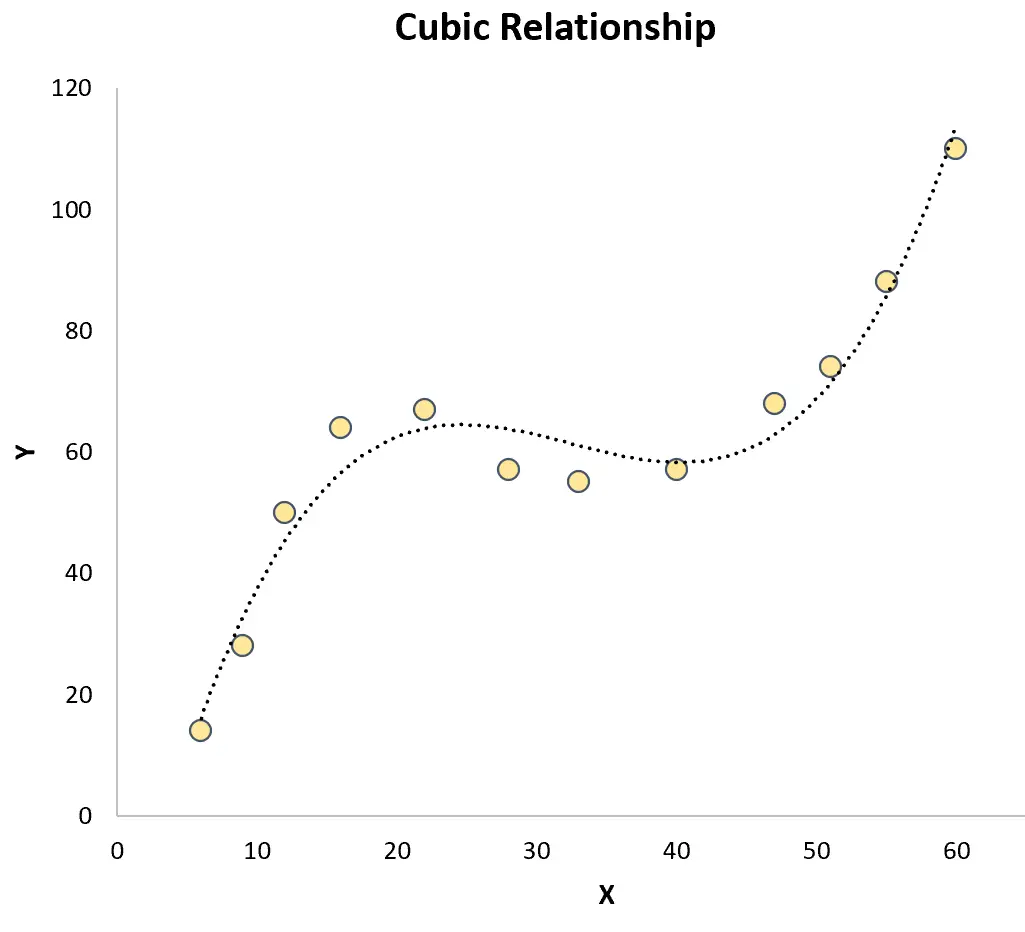
Оба они контрастируют с простой линейной регрессией , в которой связь между переменной-предиктором и переменной ответа является линейной:
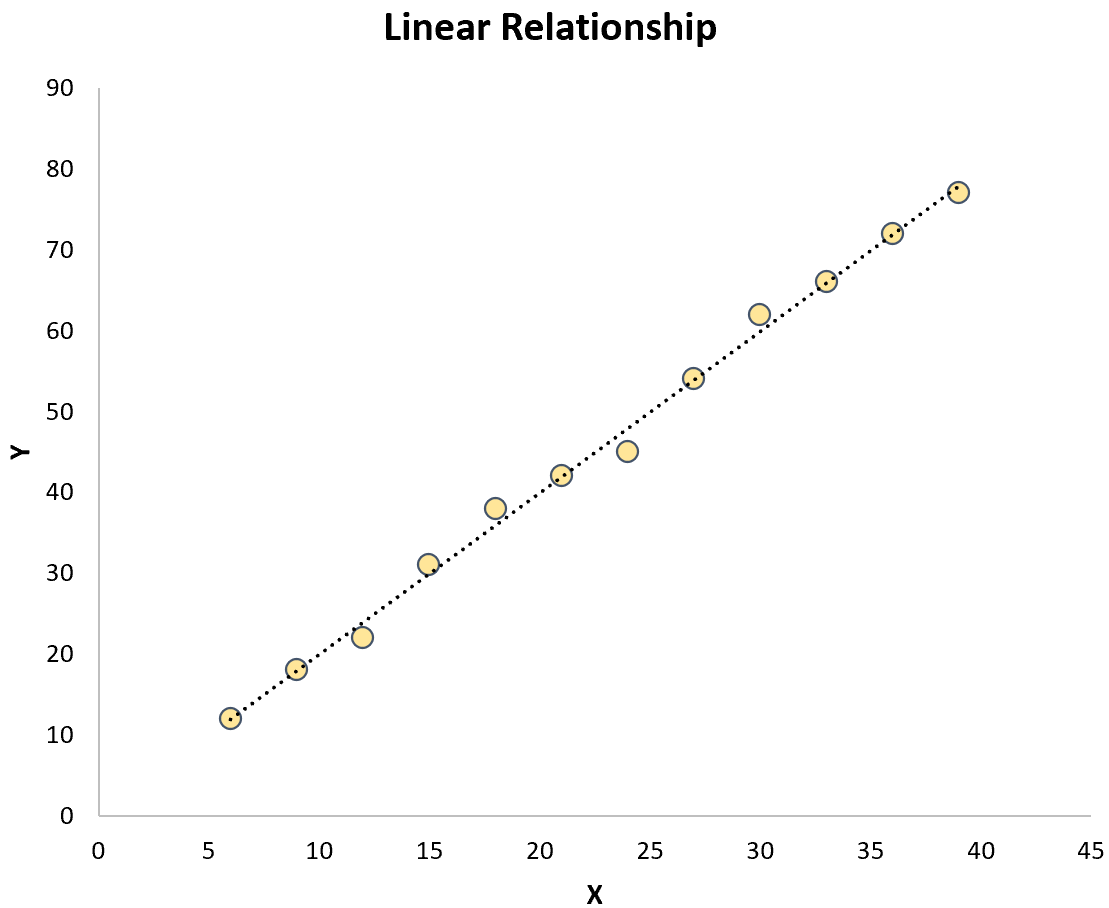
Формула для моделей криволинейной регрессии
Простая модель линейной регрессии пытается подогнать набор данных по следующей формуле:
ŷ = β 0 + β 1 x
Золото:
- ŷ: переменная ответа
- β 0 , β 1 : Коэффициенты регрессии
- x: прогнозируемая переменная
Напротив, модель квадратичной регрессии использует следующую формулу:
ŷ = β 0 + β 1 x + β 2 x 2
Модель кубической регрессии использует следующую формулу:
ŷ = β 0 + β 1 x + β 2 x 2 + β 3 x 3
Более общее название, данное моделям регрессии, включающим показатели степени, — полиномиальная регрессия , которая принимает следующую формулу:
ŷ = β 0 + β 1 x + β 2 x 2 + … + β k x k
Значение k указывает степень полинома. Хотя степень может быть любым положительным числом, на практике мы редко подбираем модели полиномиальной регрессии со степенью выше 3 или 4.
Используя показатели степени в формуле модели регрессии, модели полиномиальной регрессии могут соответствовать наборам данных кривыми , а не прямыми линиями.
Когда использовать криволинейную регрессию
Самый простой способ узнать, следует ли вам использовать криволинейную регрессию, — это создать диаграмму рассеяния переменной-предиктора и переменной отклика.
Если диаграмма рассеяния показывает линейную связь между двумя переменными, вероятно, подойдет простая линейная регрессия.
Однако если диаграмма рассеяния показывает квадратичную, кубическую или другую криволинейную структуру между предиктором и переменной ответа, то, вероятно, более целесообразным будет использовать криволинейную регрессию.
Вы также можете подогнать простую модель линейной регрессии и модель криволинейной регрессии и сравнить подобранные значения R-квадрата каждой модели, чтобы определить, какая модель лучше всего соответствует данным.
Скорректированный R-квадрат полезен, поскольку он показывает, какая часть дисперсии переменной отклика может быть объяснена предикторной переменной (переменными), скорректированной с учетом количества предикторных переменных в модели.
В целом модель с самым высоким скорректированным значением R-квадрата лучше соответствует набору данных.
Дополнительные ресурсы
В следующих руководствах объясняется, как выполнять полиномиальную регрессию в различных статистических программах:
Введение в полиномиальную регрессию
Как выполнить полиномиальную регрессию в Excel
Как выполнить полиномиальную регрессию в Python
Как выполнить полиномиальную регрессию в R