Что такое кривые плотности? (объяснение и примеры)
Кривая плотности — это кривая на графике, которая представляет распределение значений в наборе данных. Это полезно по трем причинам:
1. Кривая плотности дает нам хорошее представление о «форме» распределения, в том числе о том, имеет ли распределение один или несколько «пиков» значений частоты и смещено ли распределение влево. или вправо. ВЕРНО. .
2. Кривая плотности позволяет нам визуально увидеть, где соотносятся среднее значение и медиана распределения.
3. Кривая плотности позволяет нам визуально увидеть, какой процент наблюдений в наборе данных попадает между разными значениями.
Наиболее известной кривой плотности является колоколообразная кривая, которая представляет собой нормальное распределение .
Чтобы лучше понять кривые плотности, рассмотрим следующий пример.
Пример: создание и интерпретация кривой плотности
Допустим, у нас есть следующий набор данных, который показывает высоту 20 различных растений (в дюймах) на определенном поле:
4, 5, 5, 6, 6, 6, 6, 7, 7, 7, 7, 7, 8, 8, 8, 9, 9, 9, 2, 2
Если бы мы создали простую гистограмму для отображения относительных частот каждого значения, она выглядела бы так:
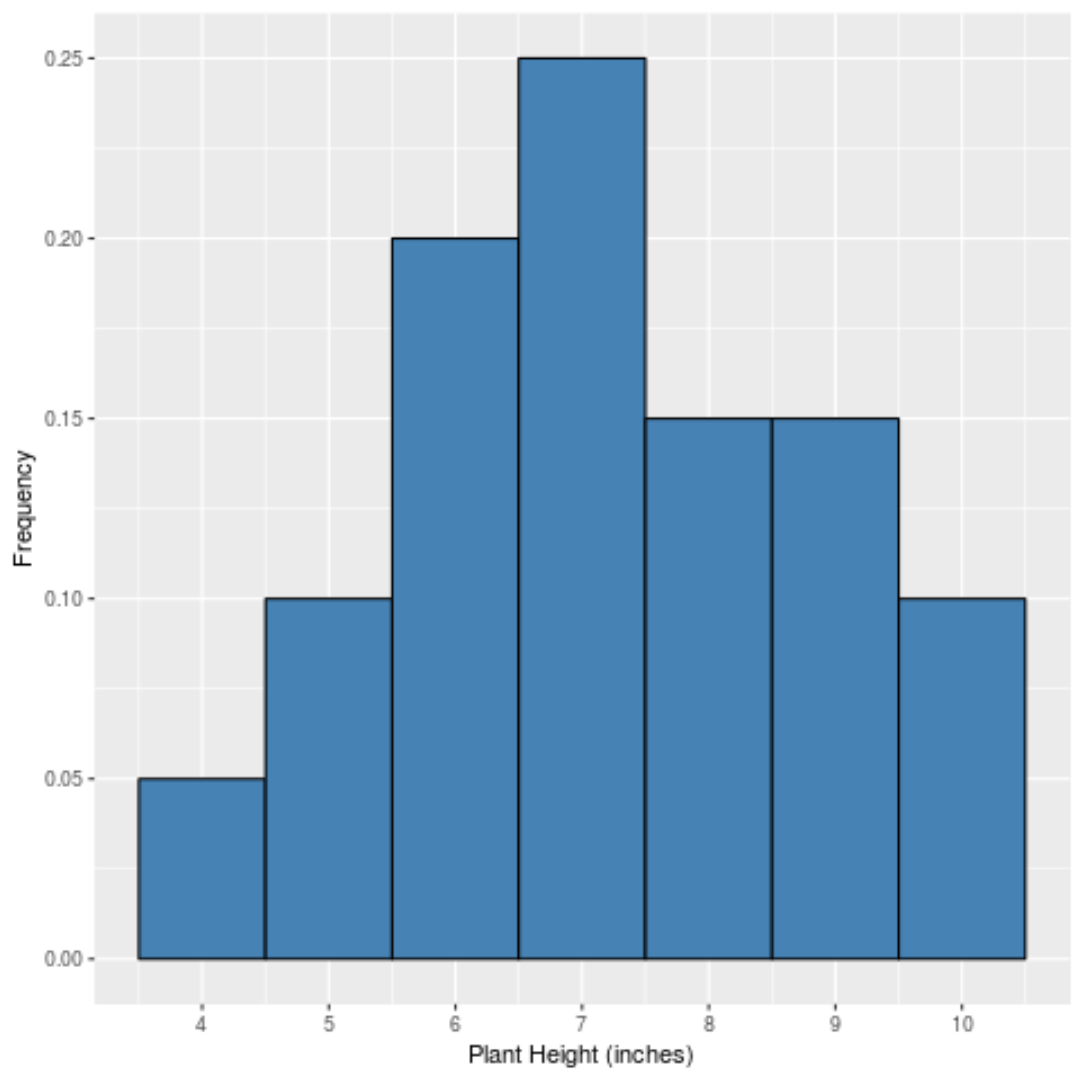
Ось X показывает значение данных, а ось Y показывает относительную частоту (например, значение «7» появляется 5 раз из 20 общих значений в наборе данных, поэтому оно имеет относительную частоту 25% или 0,25 .
И если бы мы создали кривую плотности , чтобы отразить «форму» этого распределения, она выглядела бы так:
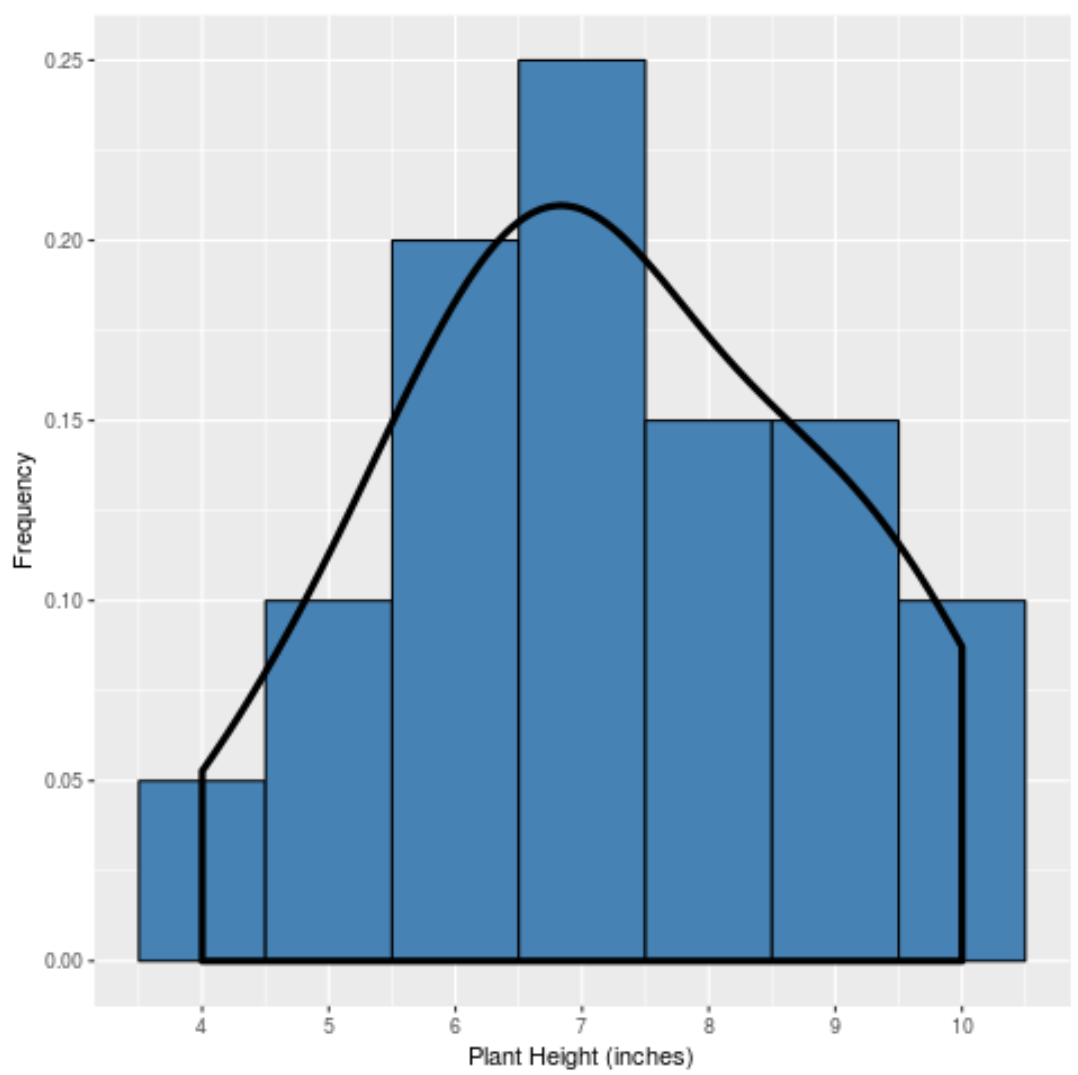
Кривая имеет наивысшую точку вблизи центра распределения, потому что именно там находится большинство значений. Он также является самым низким вблизи концов распределения, поскольку меньшее количество растений принимает эти значения (например, высота 4 дюйма или 10 дюймов).
Как интерпретировать кривые плотности
Кривые плотности бывают разных форм и размеров и позволяют нам быстро получить визуальное представление о распределении значений в заданном наборе данных. Они особенно полезны, чтобы помочь нам визуализировать:
1. Асимметрия
Асимметрия — это способ описания симметрии распределения. Кривые плотности позволяют нам быстро увидеть, наклонен ли график влево, вправо или не имеет наклона:
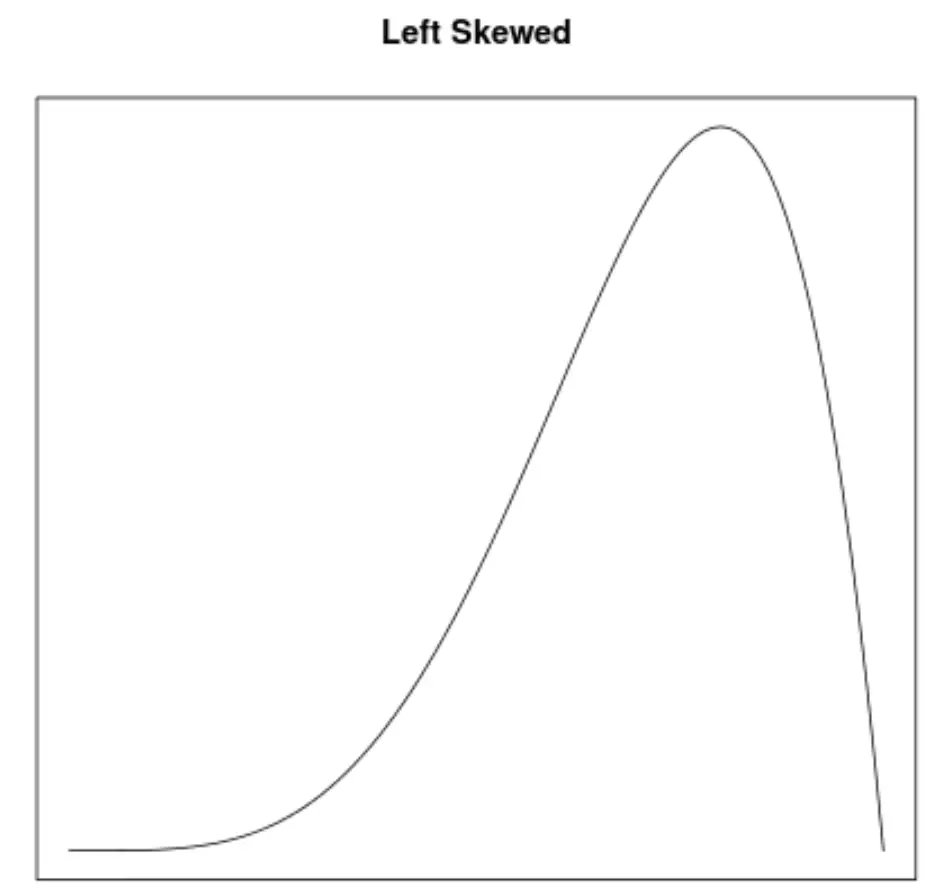
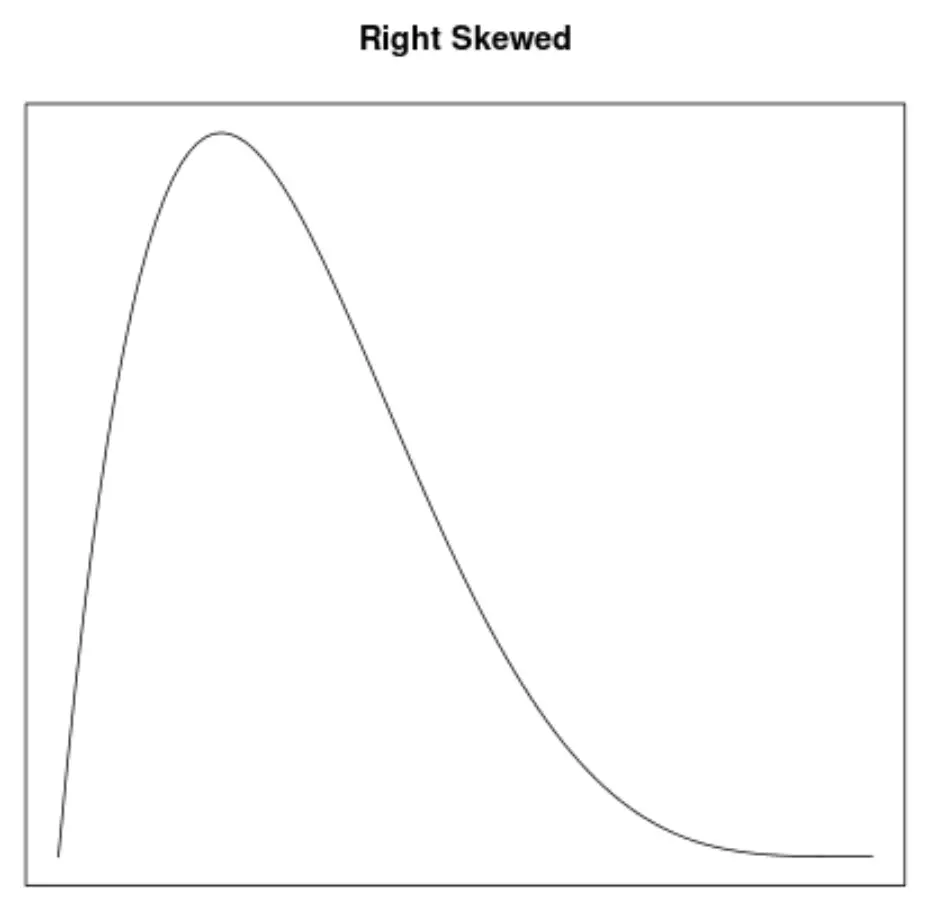
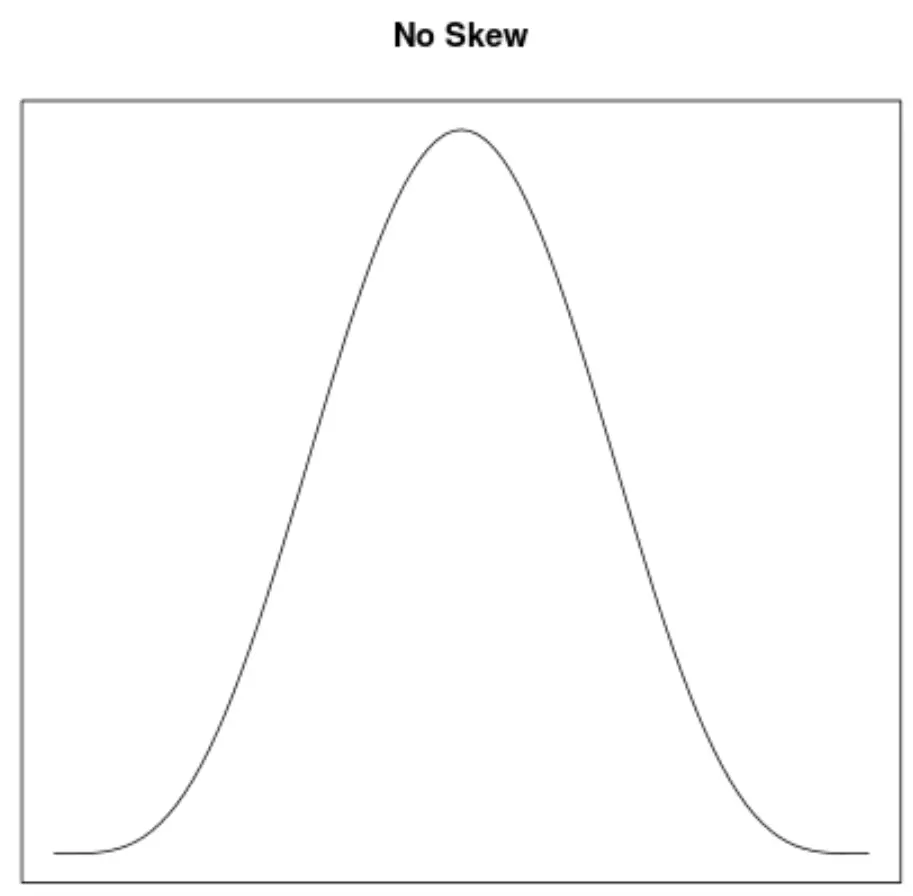
2. Расположение среднего и медианы
Основываясь на асимметрии кривой плотности, мы можем быстро определить, какое значение больше в данном распределении: среднее или медиана. Особенно:
- Если кривая плотности остается асимметричной , то среднее значение ниже медианы.
- Если кривая плотности наклонена вправо , то среднее значение больше медианы.
- Если кривая плотности не имеет асимметрии , то среднее значение равно медиане.
3. Количество пиков
Кривые плотности также позволяют нам быстро увидеть, сколько «пиков» имеется в данном распределении. В каждом из приведенных выше примеров распределения имели только один пик, поэтому мы бы описали эти распределения как унимодальные .
Однако некоторые распределения могут иметь два пика, которые мы называем бимодальными распределениями . А в редких случаях мы также можем иметь мультимодальные распределения с двумя и более пиками.
Просто создав кривую плотности для данного набора данных, мы можем быстро увидеть, сколько пиков имеется в распределении.
Свойства кривых плотности
Кривые плотности обладают следующими свойствами:
- Площадь под кривой всегда в сумме равна 100%.
- Кривая никогда не опустится ниже оси X.
Помните об этих двух фактах при создании или интерпретации кривых плотности для различных распределений.
Дополнительные ресурсы
Введение в гистограммы относительных частот
Как создать колоколообразную кривую в Excel
Как создать колоколообразную кривую в Python