Лассо-регрессия в r (шаг за шагом)
Лассо-регрессия — это метод, который мы можем использовать для подбора модели регрессии, когда в данных присутствует мультиколлинеарность .
Короче говоря, регрессия наименьших квадратов пытается найти оценки коэффициентов, которые минимизируют остаточную сумму квадратов (RSS):
RSS = Σ(y i – ŷ i )2
Золото:
- Σ : греческий символ, означающий сумму.
- y i : фактическое значение ответа для i-го наблюдения
- ŷ i : прогнозируемое значение ответа на основе модели множественной линейной регрессии.
И наоборот, лассо-регрессия стремится минимизировать следующее:
RSS + λΣ|β j |
где j изменяется от 1 до p переменных-предикторов и λ ≥ 0.
Этот второй член в уравнении известен как штраф за снятие средств . В лассо-регрессии мы выбираем значение λ, которое дает минимально возможный тест MSE (среднеквадратическая ошибка).
В этом руководстве представлен пошаговый пример выполнения лассо-регрессии в R.
Шаг 1. Загрузите данные
В этом примере мы будем использовать встроенный набор данных R под названием mtcars . Мы будем использовать hp в качестве переменной ответа и следующие переменные в качестве предикторов:
- миль на галлон
- масса
- дерьмо
- qsec
Для выполнения лассо-регрессии мы будем использовать функции из пакета glmnet . Этот пакет требует, чтобы переменная ответа была вектором, а набор переменных-предикторов принадлежал к классу data.matrix .
Следующий код показывает, как определить наши данные:
#define response variable
y <- mtcars$hp
#define matrix of predictor variables
x <- data.matrix(mtcars[, c('mpg', 'wt', 'drat', 'qsec')])
Шаг 2. Подберите модель регрессии Лассо
Далее мы воспользуемся функцией glmnet() , чтобы соответствовать модели регрессии лассо, и укажем Alpha=1 .
Обратите внимание, что установка альфа, равная 0, эквивалентна использованию гребневой регрессии , а установка альфа на значение от 0 до 1 эквивалентна использованию эластичной сети.
Чтобы определить, какое значение использовать для лямбды, мы выполним k-кратную перекрестную проверку и определим значение лямбды, которое дает наименьшую среднеквадратическую ошибку теста (MSE).
Обратите внимание, что функция cv.glmnet() автоматически выполняет k-кратную перекрестную проверку, используя k = 10 раз.
library (glmnet)
#perform k-fold cross-validation to find optimal lambda value
cv_model <- cv. glmnet (x, y, alpha = 1 )
#find optimal lambda value that minimizes test MSE
best_lambda <- cv_model$ lambda . min
best_lambda
[1] 5.616345
#produce plot of test MSE by lambda value
plot(cv_model)
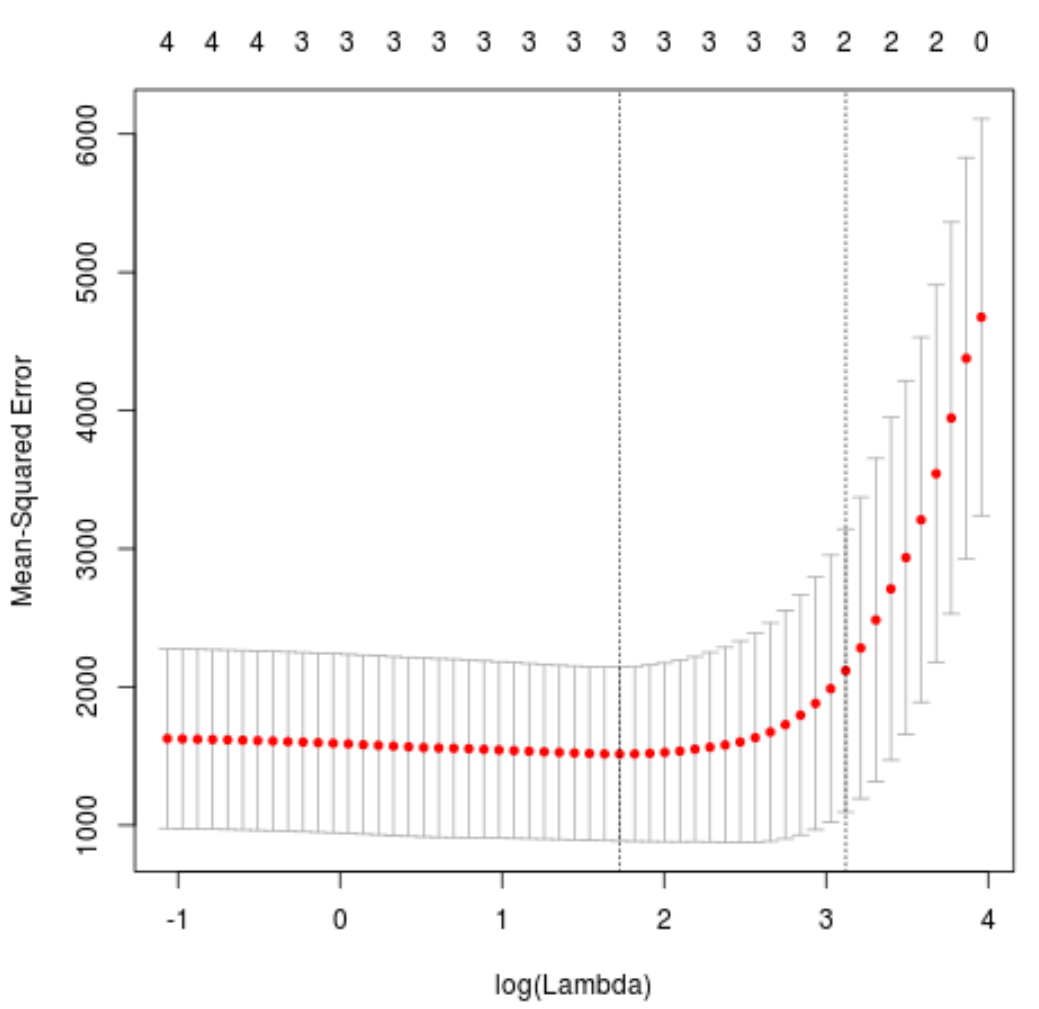
Значение лямбда, которое минимизирует тест MSE, оказывается равным 5,616345 .
Шаг 3. Анализ окончательной модели
Наконец, мы можем проанализировать окончательную модель, созданную по оптимальному значению лямбда.
Мы можем использовать следующий код для получения оценок коэффициентов для этой модели:
#find coefficients of best model
best_model <- glmnet(x, y, alpha = 1 , lambda = best_lambda)
coef(best_model)
5 x 1 sparse Matrix of class "dgCMatrix"
s0
(Intercept) 484.20742
mpg -2.95796
wt 21.37988
drat.
qsec -19.43425
Коэффициент для предиктора drat не показан, поскольку регрессия лассо снизила коэффициент до нуля. Это означает, что его полностью исключили из модели, поскольку у него не было достаточного влияния.
Обратите внимание, что это ключевое различие между гребневой регрессией и лассо-регрессией . Ридж-регрессия сводит все коэффициенты к нулю, но лассо-регрессия может удалить предикторы из модели, полностью уменьшив коэффициенты до нуля.
Мы также можем использовать окончательную модель лассо-регрессии, чтобы делать прогнозы относительно новых наблюдений. Например, предположим, что у нас есть новый автомобиль со следующими характеристиками:
- миль на галлон: 24
- вес: 2,5
- цена: 3,5
- qсек: 18,5
Следующий код показывает, как использовать подобранную модель регрессии лассо для прогнозирования значения hp этого нового наблюдения:
#define new observation
new = matrix(c(24, 2.5, 3.5, 18.5), nrow= 1 , ncol= 4 )
#use lasso regression model to predict response value
predict(best_model, s = best_lambda, newx = new)
[1,] 109.0842
На основании введенных значений модель прогнозирует, что мощность этого автомобиля будет равна 109,0842 л.с.
Наконец, мы можем рассчитать R-квадрат модели на обучающих данных:
#use fitted best model to make predictions
y_predicted <- predict (best_model, s = best_lambda, newx = x)
#find OHS and SSE
sst <- sum ((y - mean (y))^2)
sse <- sum ((y_predicted - y)^2)
#find R-Squared
rsq <- 1 - sse/sst
rsq
[1] 0.8047064
Квадрат R оказывается равным 0,8047064 . То есть лучшая модель смогла объяснить 80,47% вариации значений ответа обучающих данных.
Полный код R, использованный в этом примере, вы можете найти здесь .