Как выполнить тест левена в spss
Тест Левена используется для определения того, имеют ли две или более группы равные дисперсии.
Он широко используется, поскольку многие статистические тесты основаны на предположении, что группы имеют равные дисперсии .
В этом руководстве объясняется, как выполнить тест Левена в SPSS.
Пример: тест Левена в SPSS
Исследователи хотят знать, приводят ли три разных удобрения к разным уровням роста растений.
Они случайным образом выбирают 30 разных растений и делят их на три группы по 10, применяя к каждой группе разные удобрения. Через месяц измеряют высоту каждого растения.
На следующем снимке экрана показан объем роста (в дюймах) каждого отдельного растения, а также количество удобрений (1, 2 или 3), которые были внесены в растение:
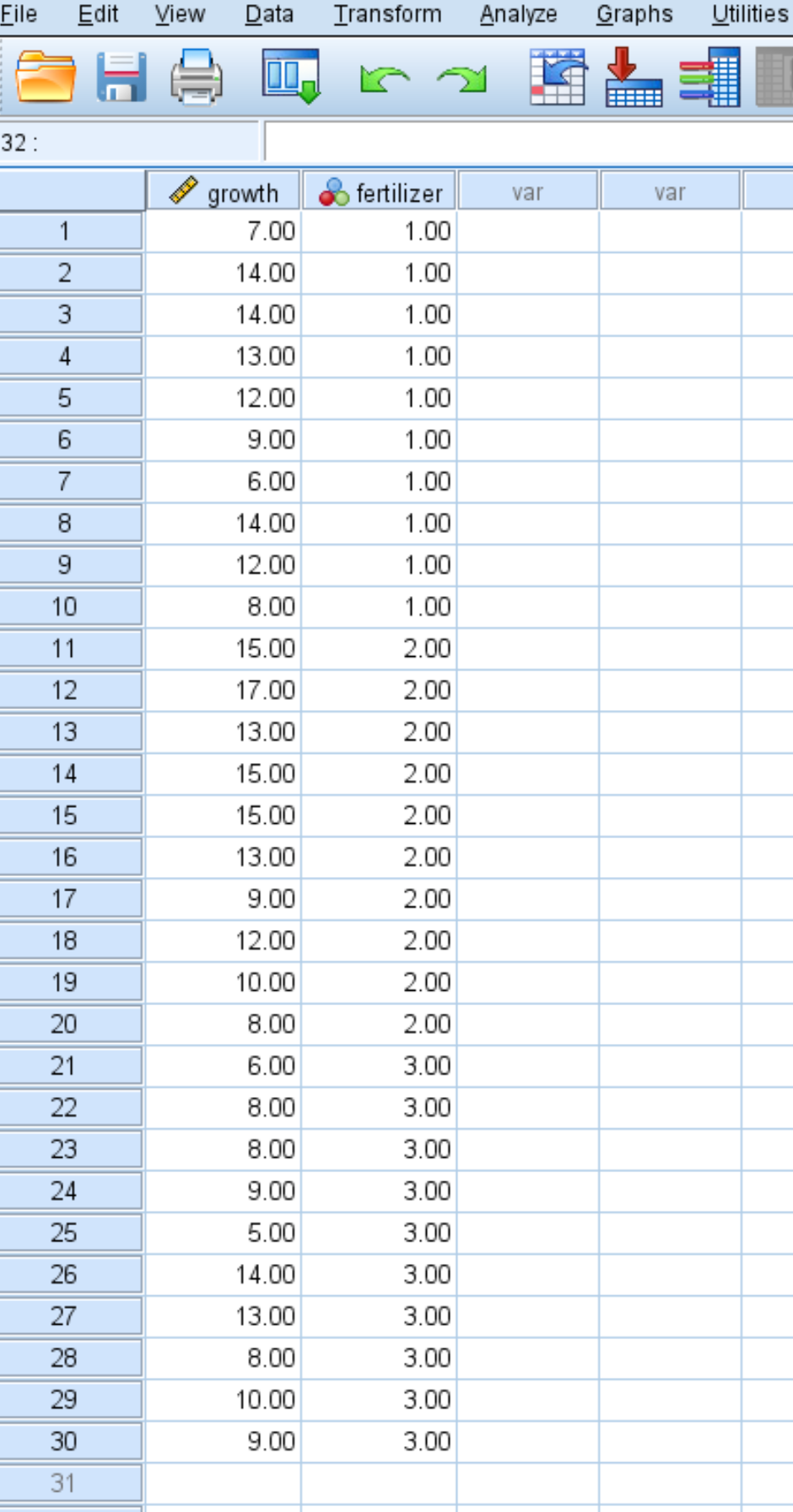
Выполните следующие шаги, чтобы выполнить тест Левена в SPSS и определить, имеют ли три группы равные дисперсии.
Шаг 1: Выберите опцию «Исследовать».
Откройте вкладку «Анализ» , затем «Описательная статистика» , затем «Исследование» :
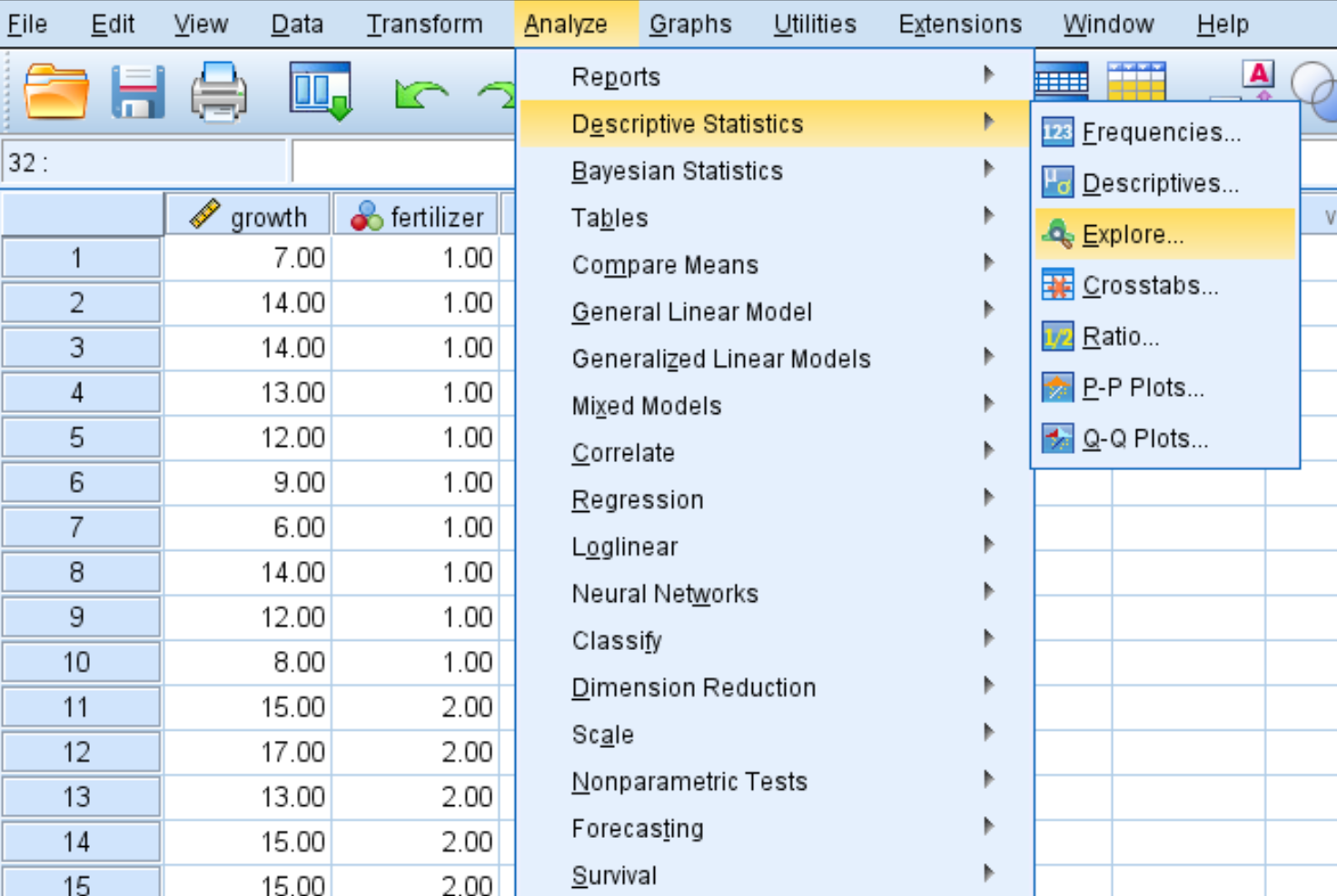
Шаг 2: Введите необходимые значения для выполнения теста.
Перетащите рост в поле под Зависимым списком и перетащите удобрение. в поле под списком факторов.
Затем нажмите «Графики» и убедитесь, что выбран параметр «Оценка мощности» . Затем нажмите «Продолжить» . Затем нажмите ОК .
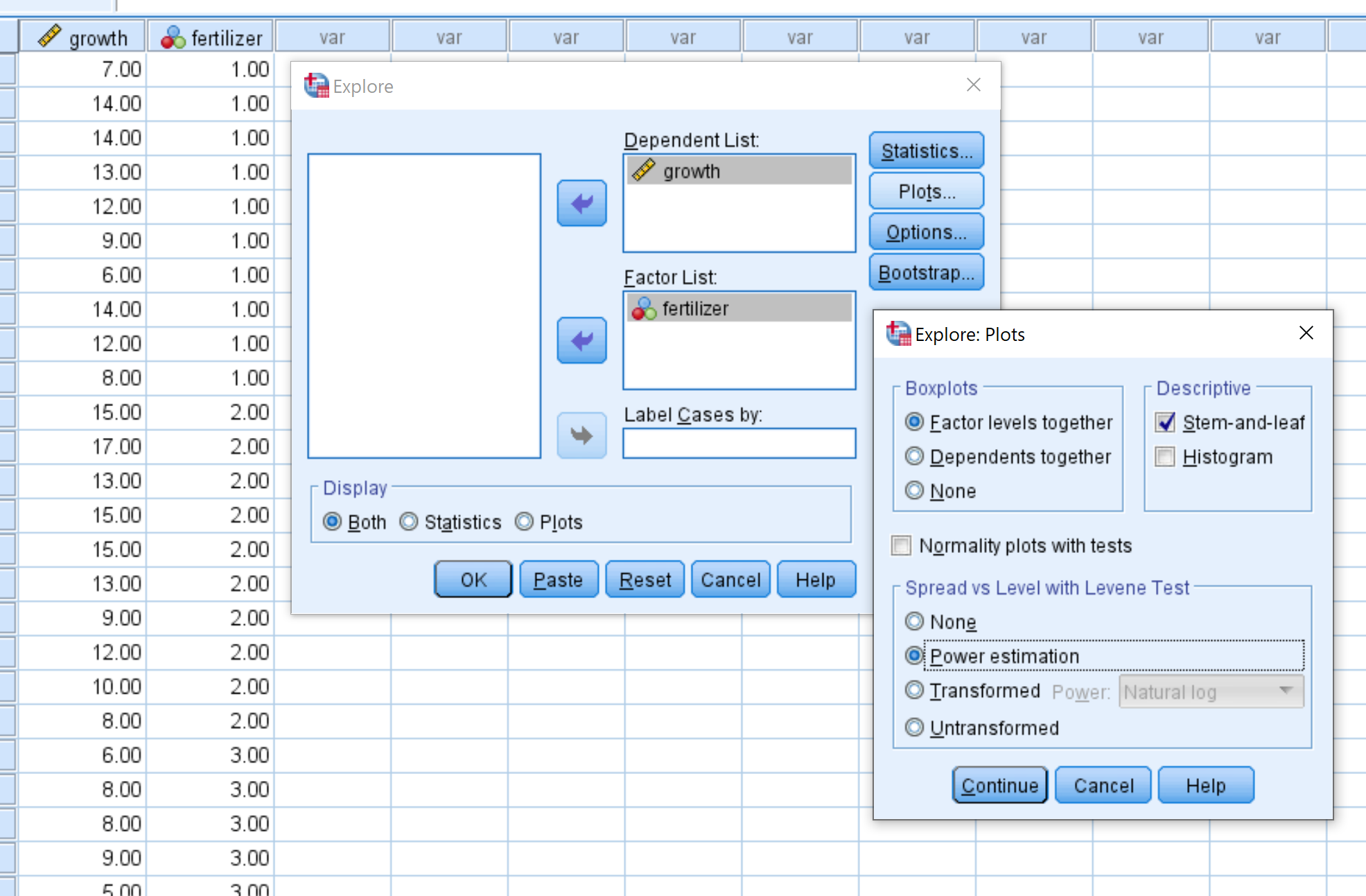
Шаг 3: Интерпретируйте результаты.
Как только вы нажмете «ОК» , отобразятся результаты теста Левена:
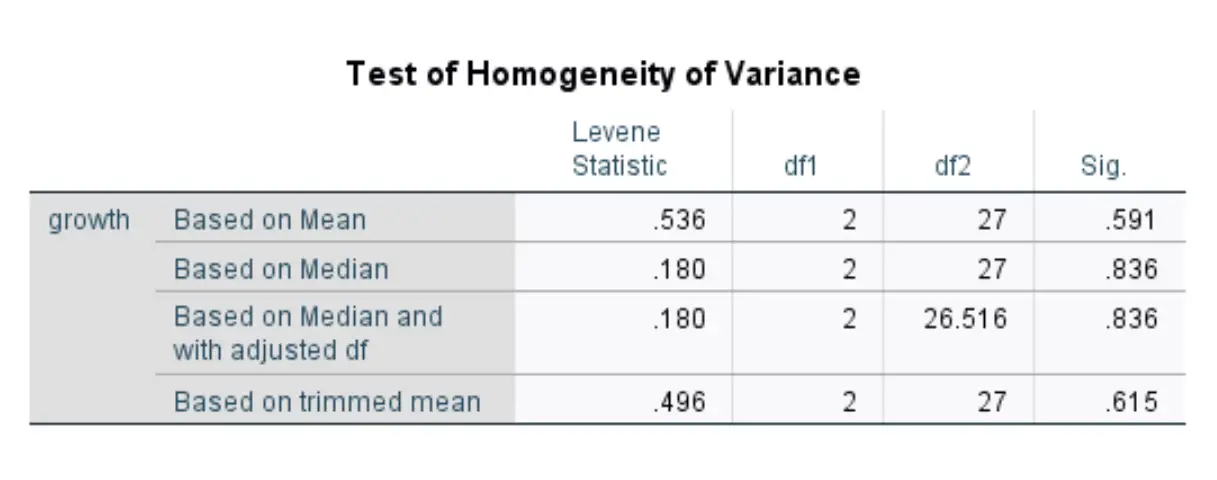
В этой таблице представлена статистика тестов для четырех различных версий теста Левена. Интересующие нас числа находятся в первой строке, где отображаются результаты теста Левена на основе среднего значения.
Статистика теста равна 0,536 , а соответствующее значение p — 0,591* .
Поскольку это значение p не меньше 0,05, мы не можем отвергнуть нулевую гипотезу.
Это означает, что у нас нет достаточных доказательств, чтобы сказать, что разница в росте растений между тремя удобрениями существенно различается.
Другими словами, все три группы имеют равные дисперсии. Если бы мы провели статистический тест (например , однофакторный дисперсионный анализ ), предполагающий, что каждая группа имеет одинаковую дисперсию, то это предположение было бы выполнено.
* Это значение p соответствует F-статистике 0,536 с числителем df = 2 и знаменателем df = 27. Это значение p также можно рассчитать с помощью калькулятора распределения F.