Как выполнить тест левена в sas
Многие статистические тесты (например , однофакторный дисперсионный анализ ) предполагают, что дисперсия между несколькими группами одинакова.
Один из способов формально проверить эту гипотезу — использовать тест Левена , который проверяет, равна ли дисперсия между двумя или более группами.
В этом тесте используются следующие предположения :
- Нулевая гипотеза (H 0 ) : дисперсия между группами одинакова.
- Альтернативная гипотеза ( HA ) : дисперсия между группами не одинакова.
Если значение p теста меньше выбранного уровня значимости, мы можем отвергнуть нулевую гипотезу и заключить, что у нас достаточно доказательств, чтобы сказать, что дисперсия между группами не равна.
В следующем примере показано, как выполнить тест Левена в SAS.
Пример: тест Левена в SAS
Допустим, у нас есть следующий набор данных в SAS, который показывает удобрения, использованные на различных растениях, и полученный в результате рост (в дюймах) для 18 растений:
/*create dataset*/ data my_data; input fertilizer $growth; datalines ; At 29 At 23 At 20 At 21 At 33 At 30 B 19 B 19 B17 B24 B25 B29 C 21 C22 C 30 C25 C24 C 33 ; run ; /*view dataset*/ proc print data =my_data;
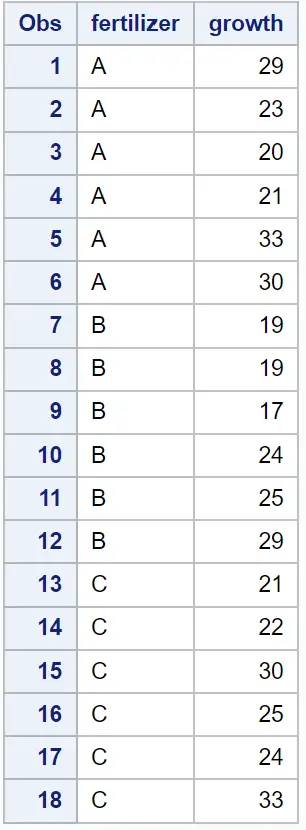
Допустим, мы хотим выполнить однофакторный дисперсионный анализ, чтобы определить, одинаков ли средний рост растений для трех разных удобрений.
Мы можем использовать следующий синтаксис в SAS для выполнения одностороннего дисперсионного анализа с помощью оператора hovtest=levene(type=abs), чтобы также выполнить тест Левена, чтобы определить, имеют ли три группы равные дисперсии:
/*perform one-way ANOVA along with Levene's test*/
proc glm data = my_data;
class fertilizer;
model growth = fertilizer;
means fertilizer / hovtest =levene(type=abs);
run ;
Первая таблица результатов показывает результаты однофакторного дисперсионного анализа:
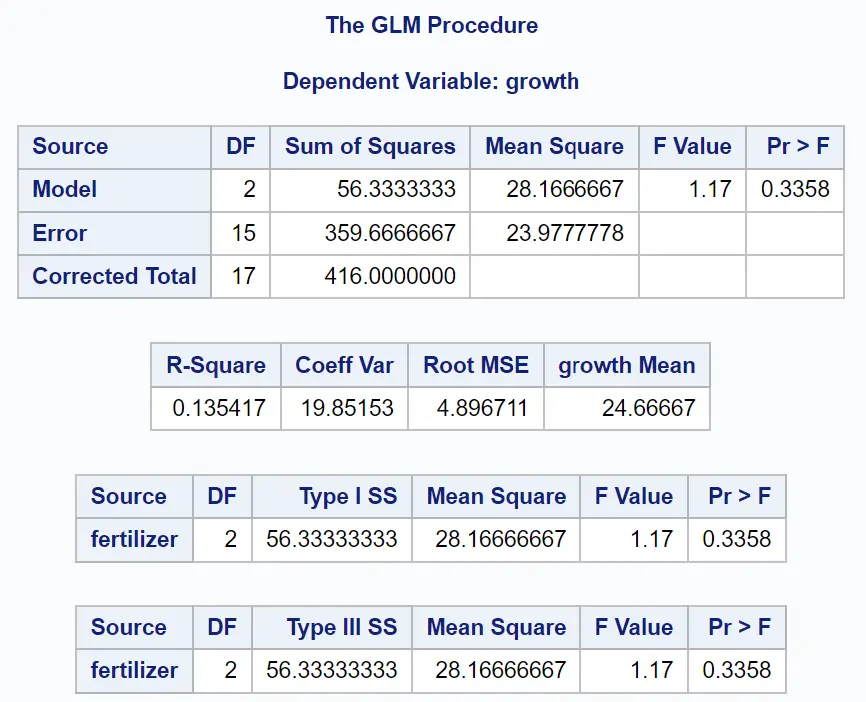
Значение p в таблице ANOVA составляет 0,3358 .
Поскольку это значение составляет не менее 0,05, мы пришли к выводу, что между тремя удобрениями нет статистически значимой разницы в среднем росте растений.
Связанный: Как интерпретировать F-значение и P-значение в ANOVA
Чтобы проверить достоверность этого результата, мы должны проверить, подтверждается ли предположение о равенстве дисперсий.
Мы можем увидеть результат теста Левена во второй таблице вывода:

Из этой таблицы мы видим, что значение p теста Левена составляет 0,6745 .
Поскольку это значение не меньше 0,05, мы не можем отвергнуть нулевую гипотезу теста.
Другими словами, мы можем предположить, что все три группы имеют равные дисперсии.
Примечание . Мы использовали аргумент type=abs в функции levene() , чтобы указать, что нам следует использовать абсолютное значение остатков при запуске теста Левена. Это согласуется с методом, используемым в других статистических программах, таких как R.
Дополнительные ресурсы
В следующих руководствах объясняется, как выполнять другие распространенные статистические тесты в SAS:
Как выполнить тест Шапиро-Уилка в SAS
Как выполнить тест Колмогорова-Смирнова в SAS
Как использовать одномерную процедуру Proc для проверки нормальности в SAS