Распределения с перекосом влево или вправо

Асимметрия — это способ описания симметрии распределения.

Распределение является перекошенным, если у него есть «хвост» на левой стороне распределения:

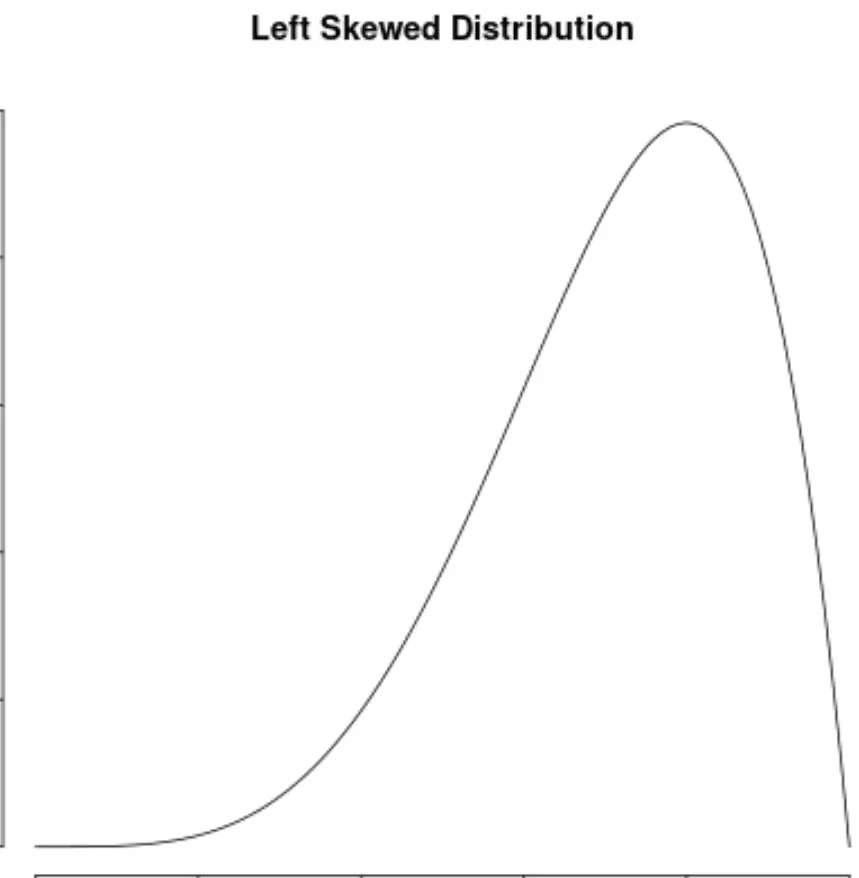
Распределение является асимметричным вправо , если у него есть «хвост» на правой стороне распределения:

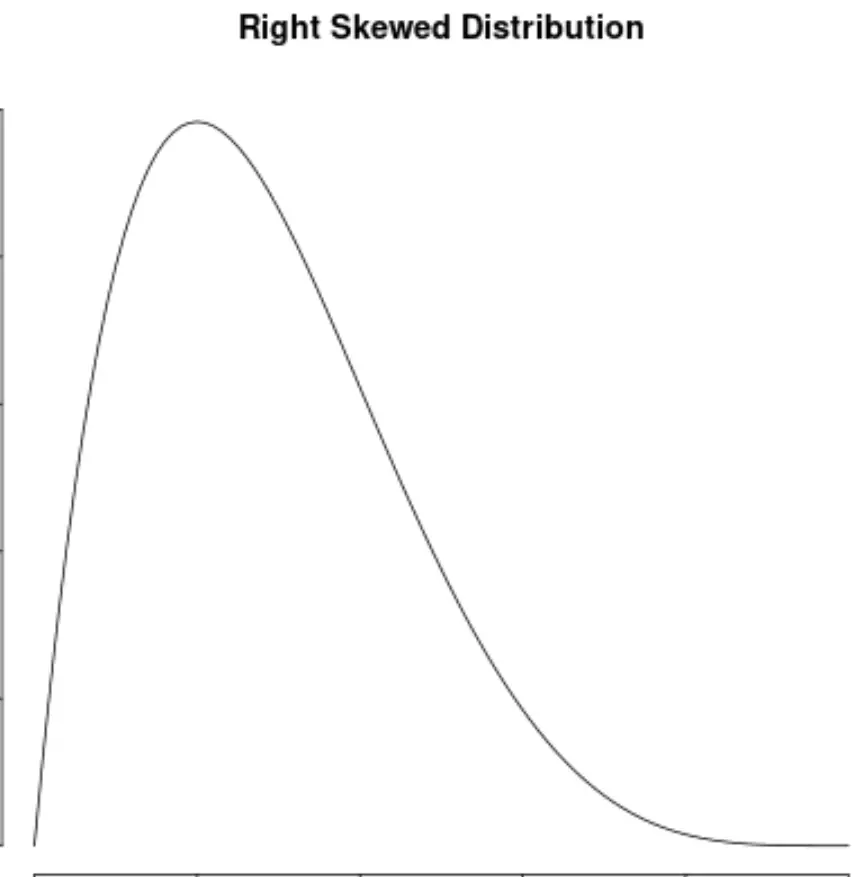
А распределение не имеет смещения , если оно симметрично с обеих сторон:

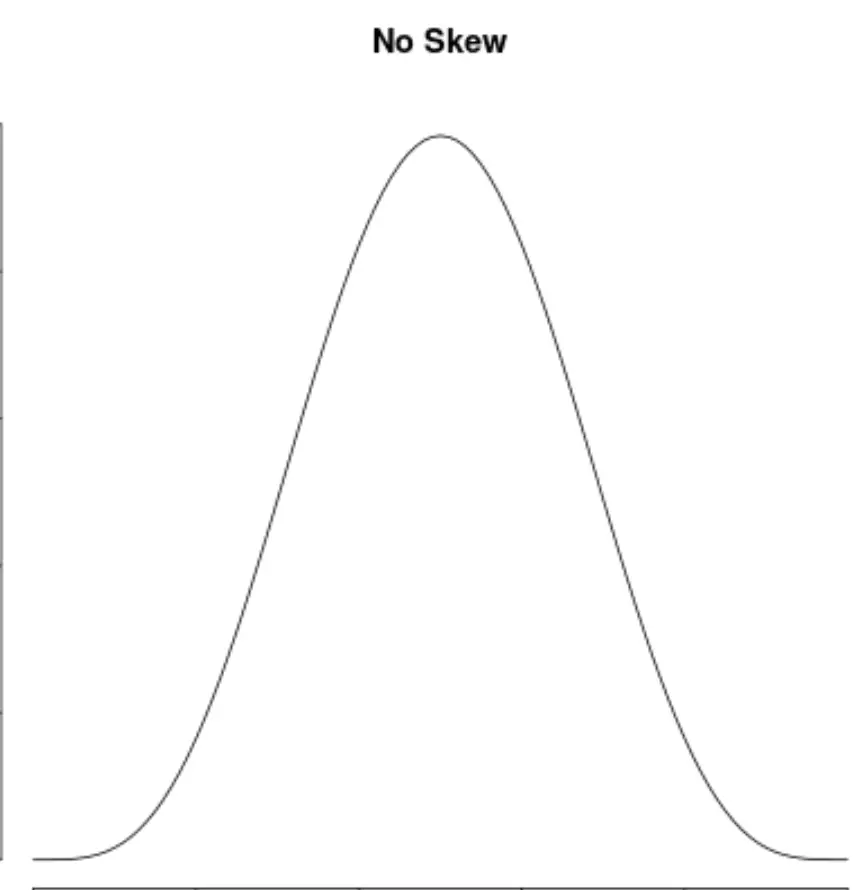
Обратите внимание, что левоасимметричные распределения иногда называют распределениями с «отрицательной асимметрией», а распределения с правой асимметрией иногда называют распределениями с «положительной асимметрией».

Свойства асимметричных распределений

На следующих диаграммах показано, где обычно находятся среднее значение, медиана и мода в различных распределениях.

Распределение с перекосом влево: Среднее < Медиана < Режим

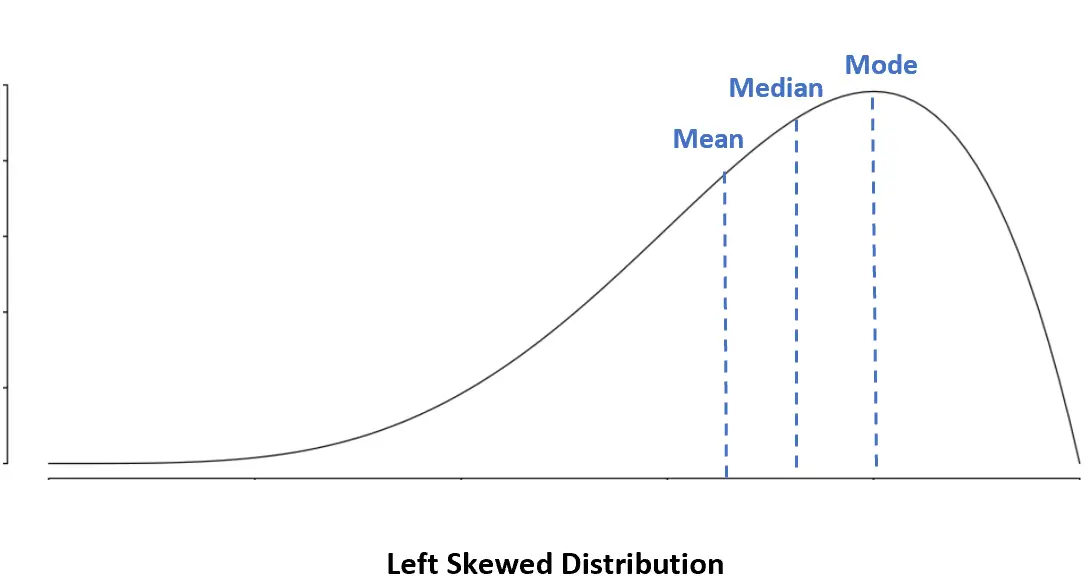
В левом распределении среднее значение меньше медианы.

Правое распределение: Режим < Медиана < Среднее значение

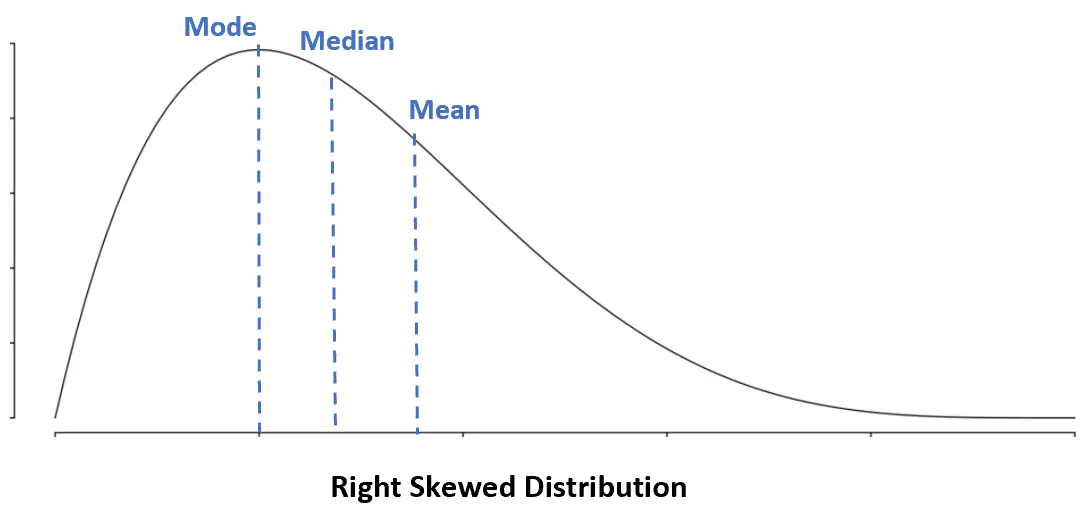
При правостороннем распределении среднее значение больше медианы.

Никакой систематической ошибки: среднее значение = медиана = режим.

В симметричном распределении среднее значение, медиана и мода равны.

Использование коробчатых диаграмм для визуализации асимметрии

Ящичковая диаграмма — это тип графика, на котором отображается пятизначная сводка набора данных, которая включает в себя:

• Минимальное значение
• Первый квартиль (25-й процентиль)
• Медианное значение
• Третий квартиль (75-й процентиль)
• Максимальное значение

Чтобы построить коробчатую диаграмму, мы рисуем прямоугольник от первого до третьего квартиля. Далее проводим вертикальную линию посередине. Наконец, рисуем «усы» квартилей до минимального и максимального значения.

Основываясь на расположении медианного значения на коробчатой диаграмме, мы можем определить, является ли распределение перекошенным влево, вправо или симметричным.

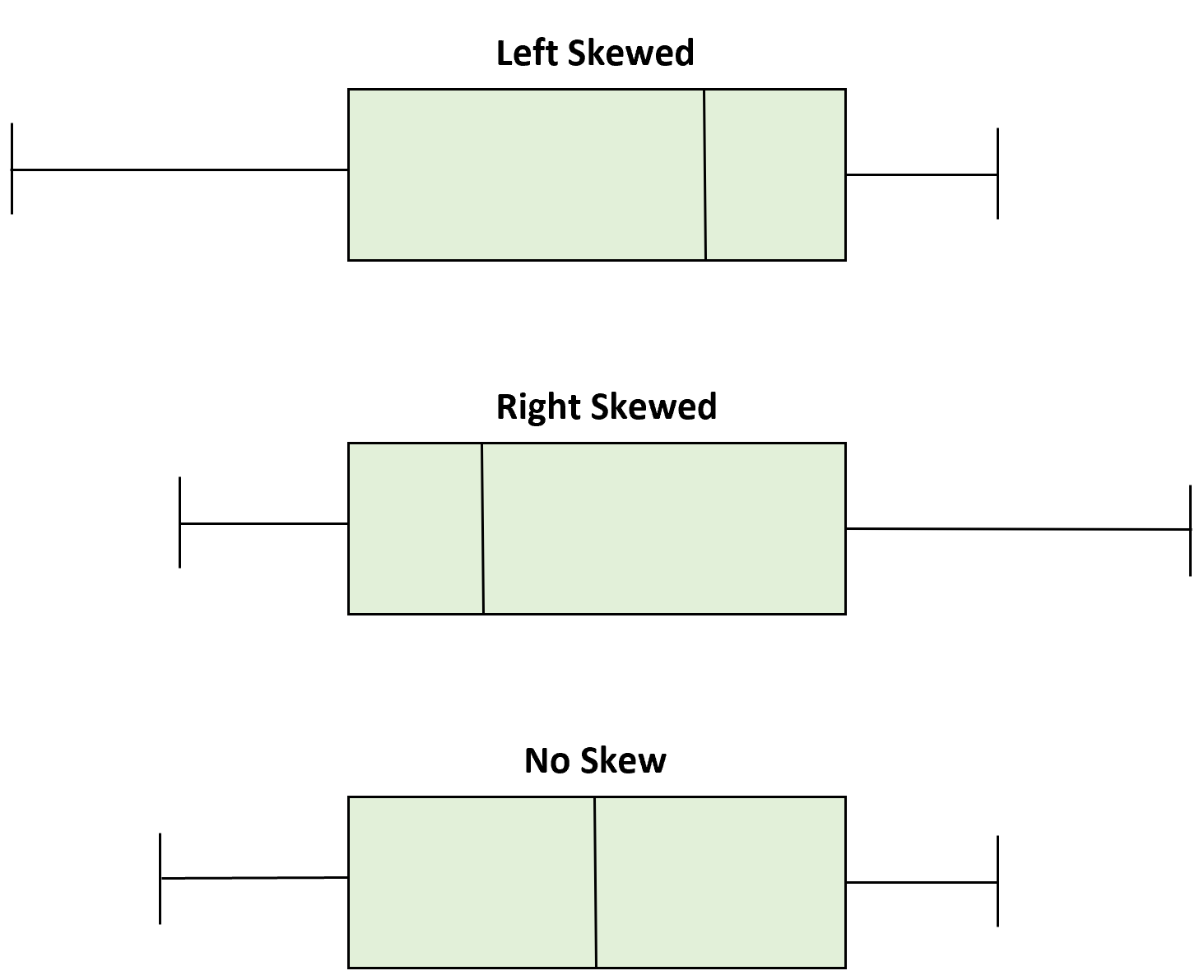
Когда медиана находится ближе к нижней части ячейки, а «ус» короче в нижней части ячейки, распределение искажается вправо.

Когда медиана находится ближе к верху ячейки, а «ус» короче в верхнем конце ячейки, распределение остается искаженным.

Когда медиана находится в середине коробки и усы примерно равны с каждой стороны, распределение симметрично.

Примеры асимметричных распределений

Вот несколько конкретных примеров асимметричного распределения.

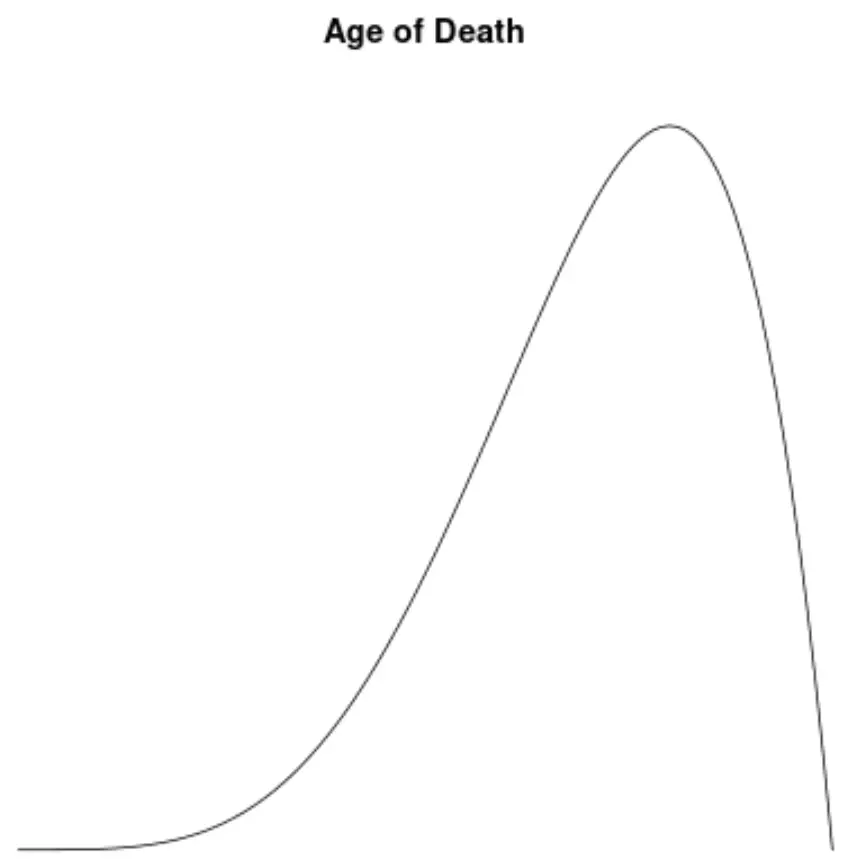
Левостороннее распределение: распределение возраста умерших.

Возрастное распределение смертности в большинстве групп населения смещено влево. Большинство людей живут в возрасте от 70 до 80 лет, и все меньше и меньше людей живут ниже этого возраста.

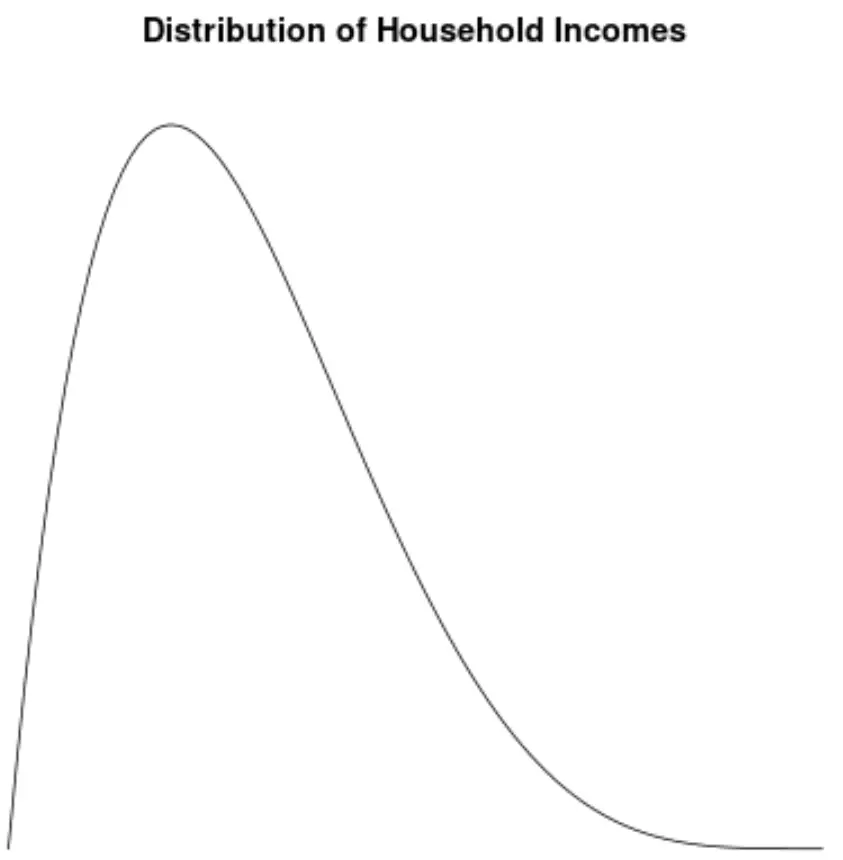
Правое распределение: распределение доходов домохозяйств.

Распределение доходов домохозяйств в Соединенных Штатах смещено вправо: большинство домохозяйств зарабатывают от 40 000 до 80 000 долларов в год, но длинный правый хвост домохозяйств зарабатывает гораздо больше.

No Skew: распределение мужских размеров.

Хорошо известно, что размеры самцов примерно нормальные и не имеют асимметрии. Например, средний рост мужчины в США составляет примерно 69,1 дюйма. Распределение по высоте примерно симметрично: одни ниже, другие выше.

Дополнительные ресурсы

5 примеров положительно асимметричных распределений
5 примеров отрицательно искаженных распределений
Как рассчитать асимметрию в Excel
Как определить асимметрию в коробчатых диаграммах