Как выполнить loess-регрессию в r (с примером)

LOESS-регрессия , иногда называемая локальной регрессией, представляет собой метод, который использует локальную корректировку для соответствия модели регрессии набору данных.

В следующем пошаговом примере показано, как выполнить регрессию LOESS в R.

Шаг 1. Создайте данные

Сначала давайте создадим следующий фрейм данных в R:

 #view DataFrame
df <- data. frame (x=c(1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14),
                 y=c(1, 4, 7, 13, 19, 24, 20, 15, 13, 11, 15, 18, 22, 27))

#view first six rows of data frame
head(df)

  xy
1 1 1
2 2 4
3 3 7
4 4 13
5 5 19
6 6 24

Шаг 2. Подберите несколько моделей регрессии LOESS.

Мы можем использовать функцию loess() , чтобы подогнать несколько моделей регрессии LOESS к этому набору данных, используя разные значения параметра интервала :

 #fit several LOESS regression models to dataset
loess50 <- loess(y ~ x, data=df, span= .5 )
smooth50 <- predict(loess50) 

loess75 <- loess(y ~ x, data=df, span= .75 )
smooth75 <- predict(loess75) 

loess90 <- loess(y ~ x, data=df, span= .9 )
smooth90 <- predict(loess90) 

#create scatterplot with each regression line overlaid
plot(df$x, df$y, pch= 19 , main=' Loess Regression Models ')
lines(smooth50, x=df$x, col=' red ')
lines(smooth75, x=df$x, col=' purple ')
lines(smooth90, x=df$x, col=' blue ')
legend(' bottomright ', legend=c(' .5 ', ' .75 ', ' .9 '),
        col=c(' red ', ' purple ', ' blue '), pch= 19 , title=' Smoothing Span ')

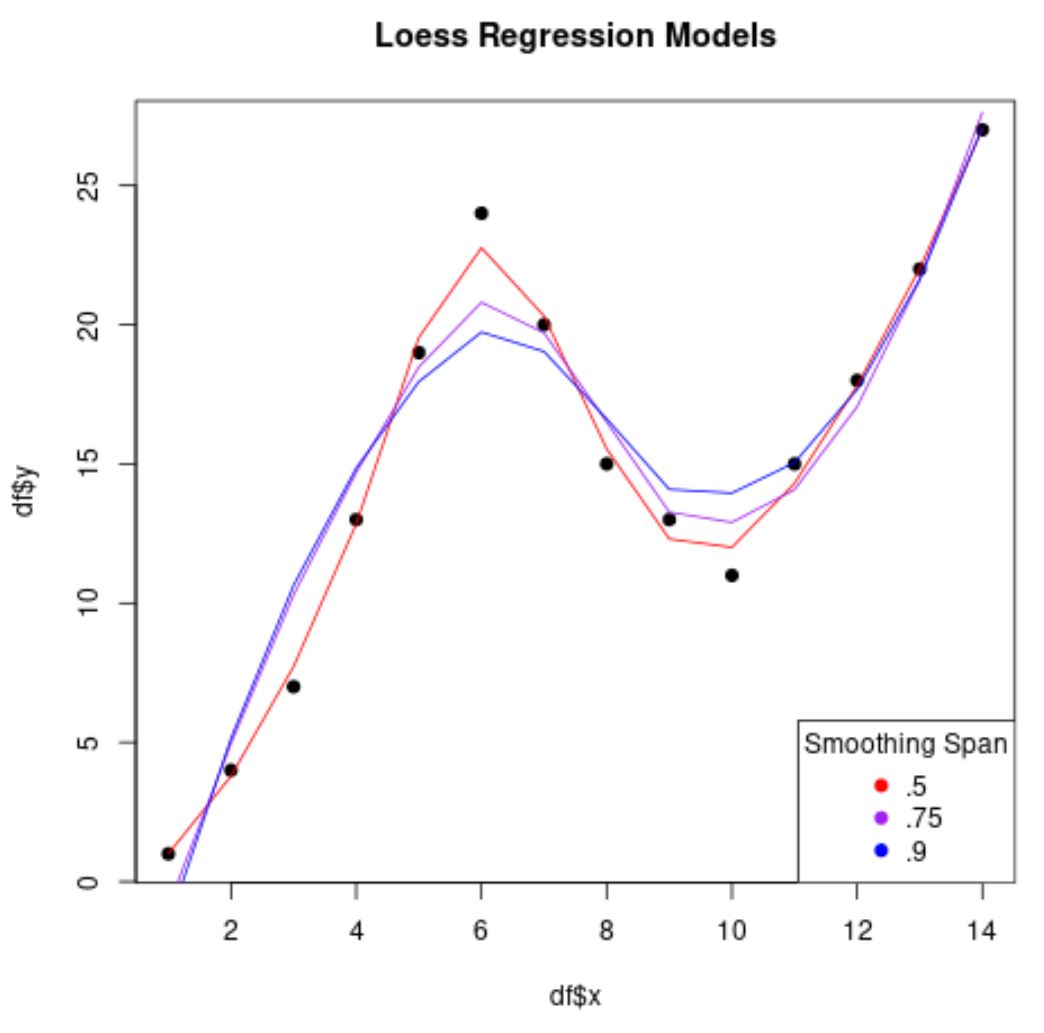
Обратите внимание: чем меньше значение, которое мы используем для диапазона , тем менее «гладкой» будет модель регрессии и тем больше она будет пытаться соответствовать точкам данных.

Шаг 3. Используйте перекрестную проверку K-Fold, чтобы найти лучшую модель

Чтобы найти оптимальное значение экстента , мы можем выполнить перекрестную проверку в k-кратном размере , используя функции из пакета Caret :

 library (caret)

#define k-fold cross validation method
ctrl <- trainControl(method = " cv ", number = 5 )
grid <- expand. grid (span = seq( 0.5 , 0.9 , len = 5 ), degree = 1 )

#perform cross-validation using smoothing spans ranging from 0.5 to 0.9
model <- train(y ~ x, data = df, method = " gamLoess ", tuneGrid=grid, trControl = ctrl)

#print results of k-fold cross-validation
print (model)

14 samples
 1 predictor

No pre-processing
Resampling: Cross-Validated (5 fold) 
Summary of sample sizes: 12, 11, 11, 11, 11 
Resampling results across tuning parameters:

  span RMSE Rsquared MAE      
  0.5 10.148315 0.9570137 6.467066
  0.6 7.854113 0.9350278 5.343473
  0.7 6.113610 0.8150066 4.769545
  0.8 17.814105 0.8202561 11.875943
  0.9 26.705626 0.7384931 17.304833

Tuning parameter 'degree' was held constant at a value of 1
RMSE was used to select the optimal model using the smallest value.
The final values used for the model were span = 0.7 and degree = 1.

Мы видим, что значение диапазона , которое дало наименьшее значение среднеквадратичной ошибки (RMSE), равно 0,7 .

Итак, для нашей окончательной модели регрессии LOESS мы бы выбрали значение 0,7 для аргумента диапазона в функции loess() .

Дополнительные ресурсы

Следующие руководства предоставляют дополнительную информацию о моделях регрессии в R:

Как выполнить простую линейную регрессию в R
Как выполнить множественную линейную регрессию в R
Как выполнить логистическую регрессию в R
Как выполнить квантильную регрессию в R
Как выполнить взвешенную регрессию в R