Excel: как использовать линейн для выполнения множественной линейной регрессии
Вы можете использовать функцию ЛИНЕЙН в Excel, чтобы подогнать модель множественной линейной регрессии к набору данных.
Эта функция использует следующий базовый синтаксис:
= LINEST ( known_y's, [known_x's], [const], [stats] )
Золото:
- known_y’s : массив известных значений y.
- известные_x : массив известных значений x.
- const : Необязательный аргумент. Если TRUE, константа b обрабатывается нормально. Если значение FALSE, константа b устанавливается в 1.
- статистика : необязательный аргумент. Если TRUE, возвращается дополнительная статистика регрессии. Если значение FALSE, дополнительная статистика регрессии не возвращается.
Следующий пошаговый пример показывает, как использовать эту функцию на практике.
Шаг 1: Введите данные
Сначала давайте введем следующий набор данных в Excel:
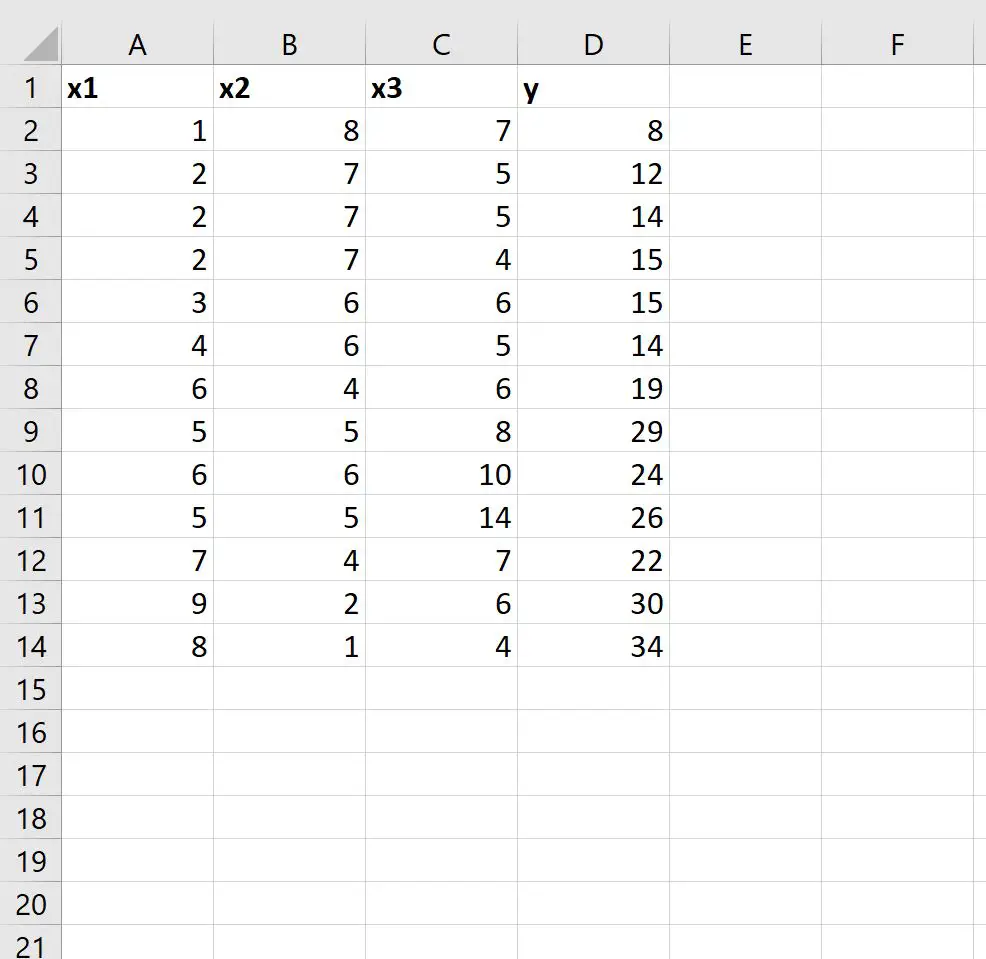
Шаг 2. Используйте ЛИНЕЙН, чтобы подобрать модель множественной линейной регрессии.
Предположим, мы хотим подогнать модель множественной линейной регрессии, используя x1 , x2 и x3 в качестве переменных-предикторов и y в качестве переменной ответа.
Для этого мы можем ввести следующую формулу в любую ячейку, соответствующую этой модели множественной линейной регрессии.
=LINEST( D2:D14 , A2:C14 )
На следующем снимке экрана показано, как использовать эту формулу на практике:
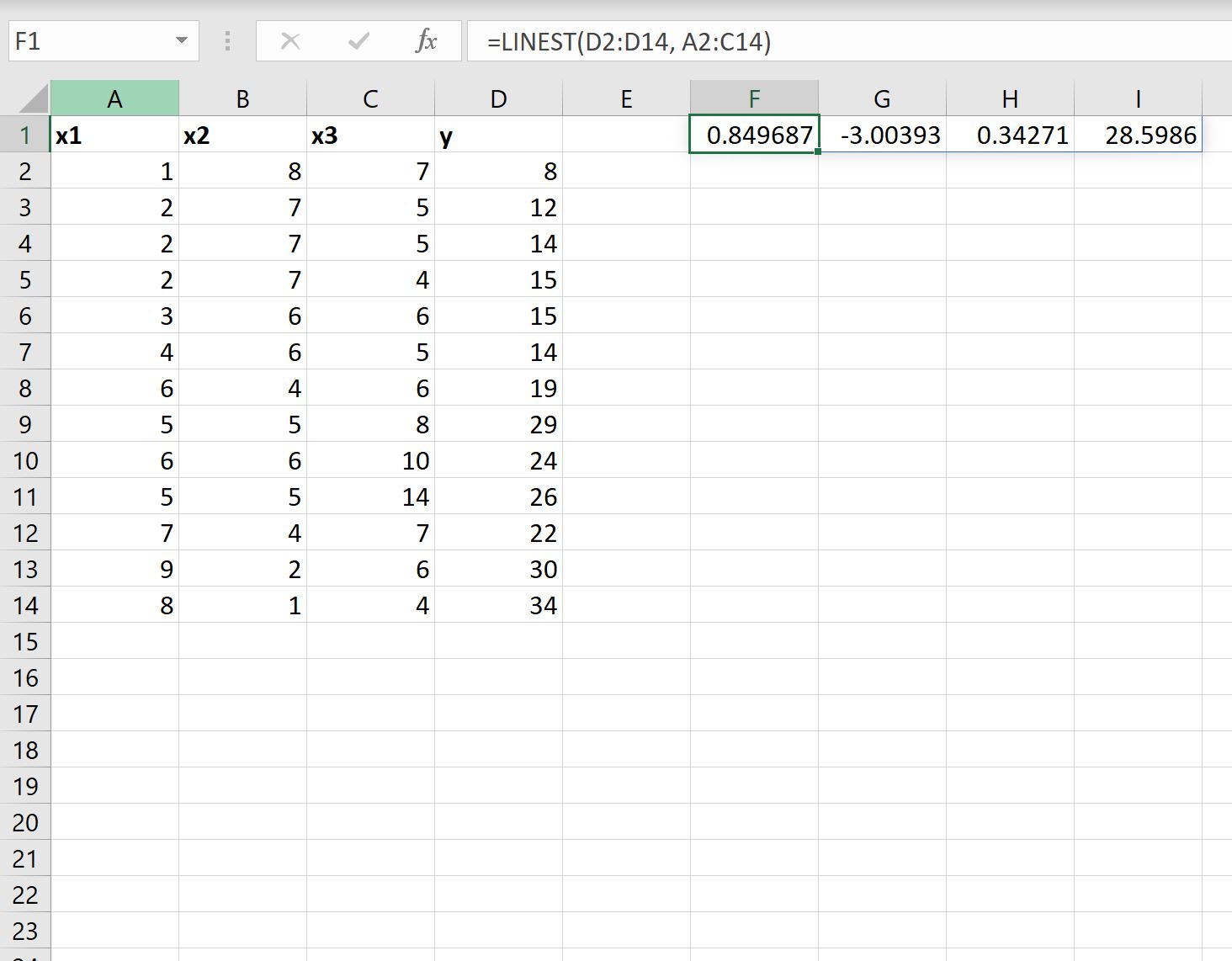
Вот как интерпретировать результат:
- Коэффициент перехвата равен 28,5986 .
- Коэффициент при x1 равен 0,34271 .
- Коэффициент при x2 равен -3,00393 .
- Коэффициент при х3 равен 0,849687 .
Используя эти коэффициенты, мы можем записать подобранное уравнение регрессии следующим образом:
у = 28,5986 + 0,34271(х1) – 3,00393(х2) + 0,849687(х3)
Шаг 3 (необязательно): просмотрите дополнительную статистику регрессии.
Мы также можем установить значение аргумента статистики в функции ЛИНЕЙН , равное ИСТИНЕ , чтобы отобразить дополнительную статистику регрессии для подобранного уравнения регрессии:
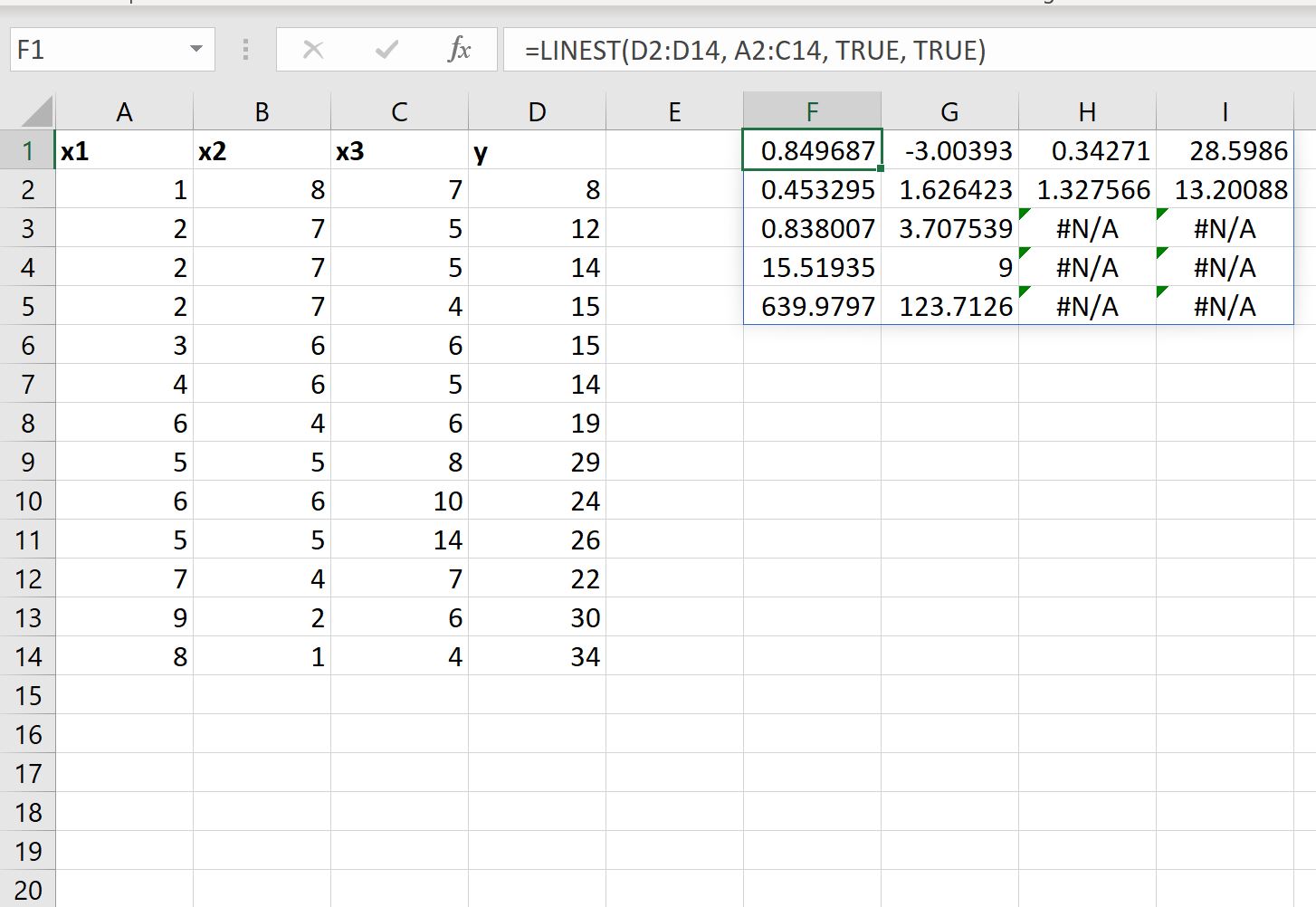
Подобранное уравнение регрессии остается прежним:
у = 28,5986 + 0,34271(х1) – 3,00393(х2) + 0,849687(х3)
Вот как интерпретировать остальные значения результата:
- Стандартная ошибка для x3 — 0,453295 .
- Стандартная ошибка для x2 — 1,626423 .
- Стандартная ошибка для x1 — 1,327566 .
- Стандартная ошибка перехвата — 13.20088 .
- R 2 модели равен 0,838007 .
- Остаточная стандартная ошибка для y равна 3,707539 .
- Общая статистика F равна 15,51925 .
- Степеней свободы 9 .
- Сумма квадратов регрессии равна 639,9797 .
- Остаточная сумма квадратов равна 123,7126 .
В общем, мерой, представляющей наибольший интерес в этой дополнительной статистике, является значение R 2 , которое представляет собой долю дисперсии переменной ответа, которую можно объяснить переменной-предиктором.
Значение R 2 может изменяться от 0 до 1.
Поскольку R 2 этой конкретной модели равен 0,838 , это говорит нам о том, что переменные-предикторы хорошо справляются с предсказанием значения переменной отклика y.
Связанный: Что такое хорошее значение R-квадрата?
Дополнительные ресурсы
В следующих руководствах объясняется, как выполнять другие распространенные операции в Excel:
Как использовать функцию ЛИНГЕСТ в Excel
Как выполнить нелинейную регрессию в Excel
Как выполнить кубическую регрессию в Excel