Линейный дискриминантный анализ в r (шаг за шагом)
Линейный дискриминантный анализ — это метод, который можно использовать, если у вас есть набор переменных-предикторов и вы хотите классифицировать переменную отклика на два или более классов.
В этом руководстве представлен пошаговый пример выполнения линейного дискриминантного анализа в R.
Шаг 1. Загрузите необходимые библиотеки
Сначала мы загрузим необходимые библиотеки для этого примера:
library (MASS)
library (ggplot2)
Шаг 2. Загрузите данные
В этом примере мы будем использовать набор данных радужной оболочки глаза , встроенный в R. Следующий код показывает, как загрузить и отобразить этот набор данных:
#attach iris dataset to make it easy to work with attach(iris) #view structure of dataset str(iris) 'data.frame': 150 obs. of 5 variables: $ Sepal.Length: num 5.1 4.9 4.7 4.6 5 5.4 4.6 5 4.4 4.9 ... $ Sepal.Width: num 3.5 3 3.2 3.1 3.6 3.9 3.4 3.4 2.9 3.1 ... $Petal.Length: num 1.4 1.4 1.3 1.5 1.4 1.7 1.4 1.5 1.4 1.5 ... $Petal.Width: num 0.2 0.2 0.2 0.2 0.2 0.4 0.3 0.2 0.2 0.1 ... $ Species: Factor w/ 3 levels "setosa","versicolor",..: 1 1 1 1 1 1 1 ...
Мы видим, что набор данных содержит 5 переменных и всего 150 наблюдений.
В этом примере мы построим модель линейного дискриминантного анализа, чтобы классифицировать, к какому виду принадлежит данный цветок.
В модели мы будем использовать следующие переменные-предикторы:
- Длина чашелистика
- Чашелистик.Ширина
- Лепесток.Длина
- Лепесток.Ширина
И мы будем использовать их для прогнозирования переменной ответа вида , которая поддерживает следующие три потенциальных класса:
- сетоза
- лишай
- Вирджиния
Шаг 3. Масштабируйте данные
Одним из ключевых предположений линейного дискриминантного анализа является то, что каждая из переменных-предикторов имеет одинаковую дисперсию. Простой способ обеспечить выполнение этого предположения — масштабировать каждую переменную так, чтобы ее среднее значение было равно 0, а стандартное отклонение — 1.
Мы можем сделать это быстро в R, используя функцию Scale() :
#scale each predictor variable (ie first 4 columns)
iris[1:4] <- scale(iris[1:4])
Мы можем использовать функцию apply() , чтобы убедиться, что каждая переменная-предиктор теперь имеет среднее значение 0 и стандартное отклонение 1:
#find mean of each predictor variable apply(iris[1:4], 2, mean) Sepal.Length Sepal.Width Petal.Length Petal.Width -4.484318e-16 2.034094e-16 -2.895326e-17 -3.663049e-17 #find standard deviation of each predictor variable apply(iris[1:4], 2, sd) Sepal.Length Sepal.Width Petal.Length Petal.Width 1 1 1 1
Шаг 4. Создайте образцы для обучения и тестирования.
Далее мы разделим набор данных на обучающий набор для обучения модели и тестовый набор для проверки модели:
#make this example reproducible set.seed(1) #Use 70% of dataset as training set and remaining 30% as testing set sample <- sample(c( TRUE , FALSE ), nrow (iris), replace = TRUE , prob =c(0.7,0.3)) train <- iris[sample, ] test <- iris[!sample, ]
Шаг 5. Настройте модель LDA
Далее мы воспользуемся функцией lda() из пакета MASS , чтобы адаптировать модель LDA к нашим данным:
#fit LDA model model <- lda(Species~., data=train) #view model output model Call: lda(Species ~ ., data = train) Prior probabilities of groups: setosa versicolor virginica 0.3207547 0.3207547 0.3584906 Group means: Sepal.Length Sepal.Width Petal.Length Petal.Width setosa -1.0397484 0.8131654 -1.2891006 -1.2570316 versicolor 0.1820921 -0.6038909 0.3403524 0.2208153 virginica 0.9582674 -0.1919146 1.0389776 1.1229172 Coefficients of linear discriminants: LD1 LD2 Sepal.Length 0.7922820 0.5294210 Sepal.Width 0.5710586 0.7130743 Petal.Length -4.0762061 -2.7305131 Petal.Width -2.0602181 2.6326229 Proportion of traces: LD1 LD2 0.9921 0.0079
Вот как интерпретировать результаты модели:
Групповые априорные вероятности: они представляют собой доли каждого вида в обучающем наборе. Например, 35,8% всех наблюдений в обучающей выборке относились к виду Virginica .
Средние группы: отображают средние значения каждой предикторной переменной для каждого вида.
Линейные дискриминантные коэффициенты: они отображают линейную комбинацию переменных-предикторов, используемых для обучения правилу принятия решения модели LDA. Например:
- LD1: 0,792 * длина чашелистика + 0,571 * ширина чашелистика – 4,076 * длина лепестка – 2,06 * ширина лепестка
- LD2: 0,529 * длина чашелистика + 0,713 * ширина чашелистика – 2,731 * длина лепестка + 2,63 * ширина лепестка
Пропорция трассировки: отображает процент разделения, достигнутый каждой линейной дискриминантной функцией.
Шаг 6. Используйте модель для прогнозирования
После того, как мы подогнали модель, используя наши обучающие данные, мы можем использовать ее для прогнозирования наших тестовых данных:
#use LDA model to make predictions on test data predicted <- predict (model, test) names(predicted) [1] "class" "posterior" "x"
Это возвращает список с тремя переменными:
- класс: предсказанный класс
- апостериорный: апостериорная вероятность того, что наблюдение принадлежит каждому классу.
- x: Линейные дискриминанты
Мы можем быстро визуализировать каждый из этих результатов для первых шести наблюдений в нашем наборе тестовых данных:
#view predicted class for first six observations in test set head(predicted$class) [1] setosa setosa setosa setosa setosa setosa Levels: setosa versicolor virginica #view posterior probabilities for first six observations in test set head(predicted$posterior) setosa versicolor virginica 4 1 2.425563e-17 1.341984e-35 6 1 1.400976e-21 4.482684e-40 7 1 3.345770e-19 1.511748e-37 15 1 6.389105e-31 7.361660e-53 17 1 1.193282e-25 2.238696e-45 18 1 6.445594e-22 4.894053e-41 #view linear discriminants for first six observations in test set head(predicted$x) LD1 LD2 4 7.150360 -0.7177382 6 7.961538 1.4839408 7 7.504033 0.2731178 15 10.170378 1.9859027 17 8.885168 2.1026494 18 8.113443 0.7563902
Мы можем использовать следующий код, чтобы увидеть, для какого процента наблюдений модель LDA правильно предсказала вид:
#find accuracy of model
mean(predicted$class==test$Species)
[1] 1
Оказывается, модель правильно предсказала вид для 100% наблюдений в нашем тестовом наборе данных.
В реальном мире модель LDA редко правильно предсказывает результаты каждого класса, но этот набор данных радужной оболочки просто построен таким образом, что алгоритмы машинного обучения имеют тенденцию работать очень хорошо.
Шаг 7: Визуализируйте результаты
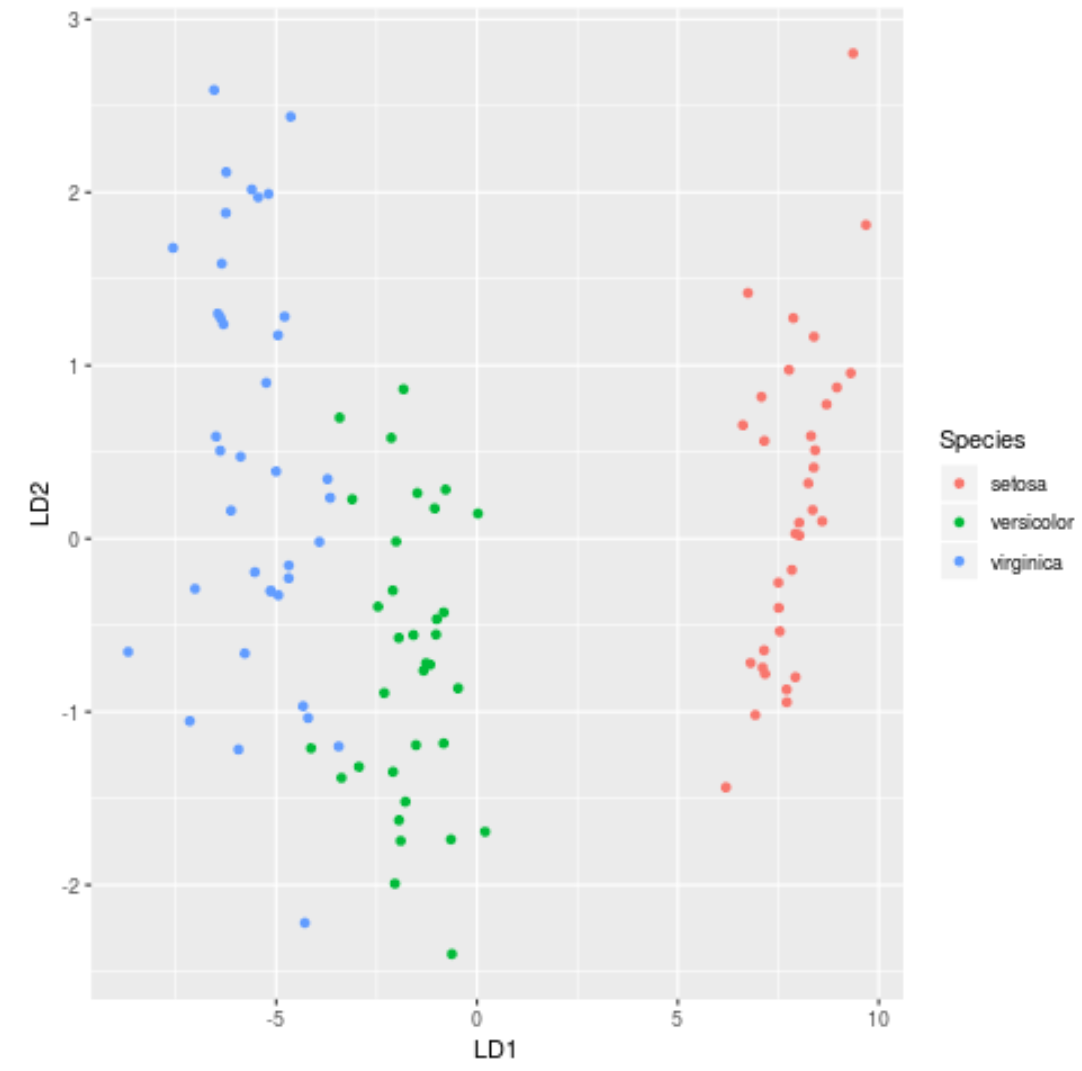
Наконец, мы можем создать график LDA, чтобы визуализировать линейные дискриминанты модели и понять, насколько хорошо она разделяет три разных вида в нашем наборе данных:
#define data to plot lda_plot <- cbind(train, predict(model)$x) #createplot ggplot(lda_plot, aes (LD1, LD2)) + geom_point( aes (color=Species))
Полный код R, используемый в этом уроке, можно найти здесь .