Как создать линию наилучшего соответствия в excel
В статистике линия наилучшего соответствия — это линия, которая лучше всего «соответствует» или описывает взаимосвязь между переменной-предиктором и переменной отклика .
В следующем пошаговом примере показано, как создать линию наилучшего соответствия в Excel.
Шаг 1: Введите данные
Сначала давайте введем следующий набор данных, который показывает количество часов, потраченных на тренировки, и общее количество очков, набранных восемью разными баскетболистами:
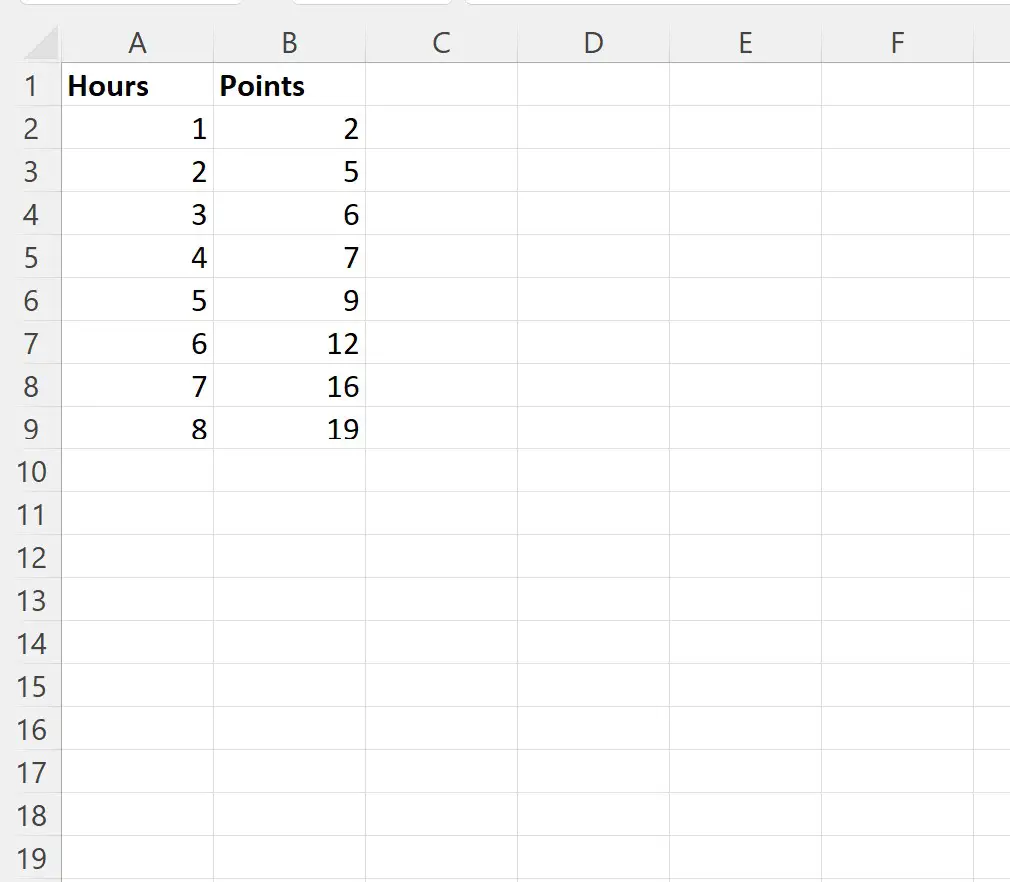
Шаг 2. Создайте диаграмму рассеяния
Далее давайте создадим диаграмму рассеяния, чтобы визуализировать связь между двумя переменными.
Для этого выделите ячейки в диапазоне A2:B9 , затем щелкните вкладку «Вставка» на верхней ленте, затем выберите параметр « Разброс» в группе «Диаграммы» :
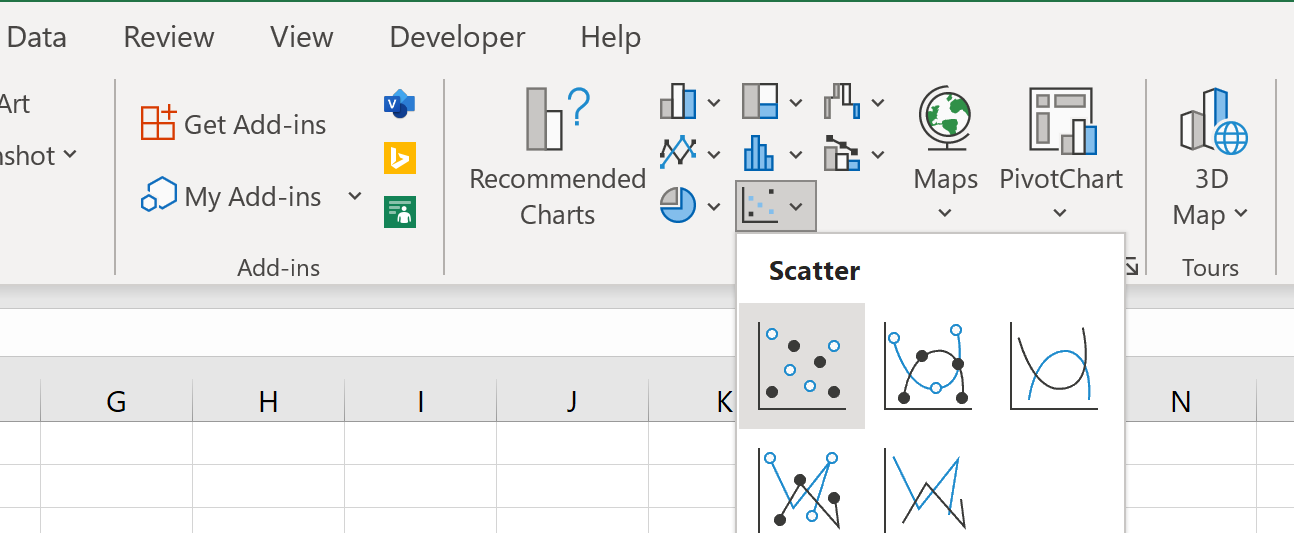
Следующее облако точек будет создано автоматически:
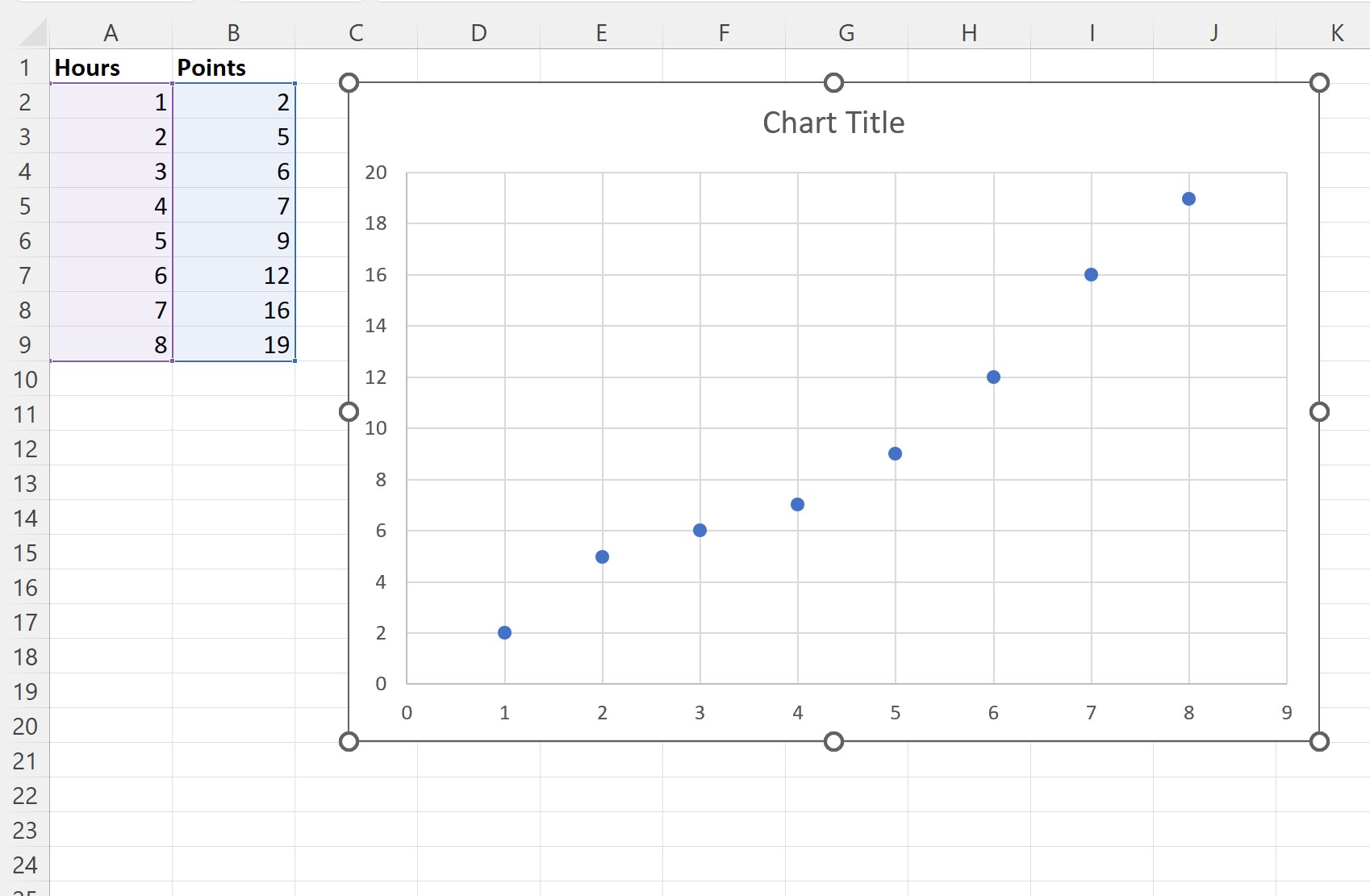
Шаг 3. Добавьте наиболее подходящую линию.
Чтобы добавить линию наилучшего соответствия на диаграмму рассеяния, щелкните в любом месте графика, затем щелкните зеленый знак плюса (+), который появляется в правом верхнем углу графика.
Затем щелкните стрелку рядом с надписью «Линия тренда» и выберите «Дополнительные параметры» :
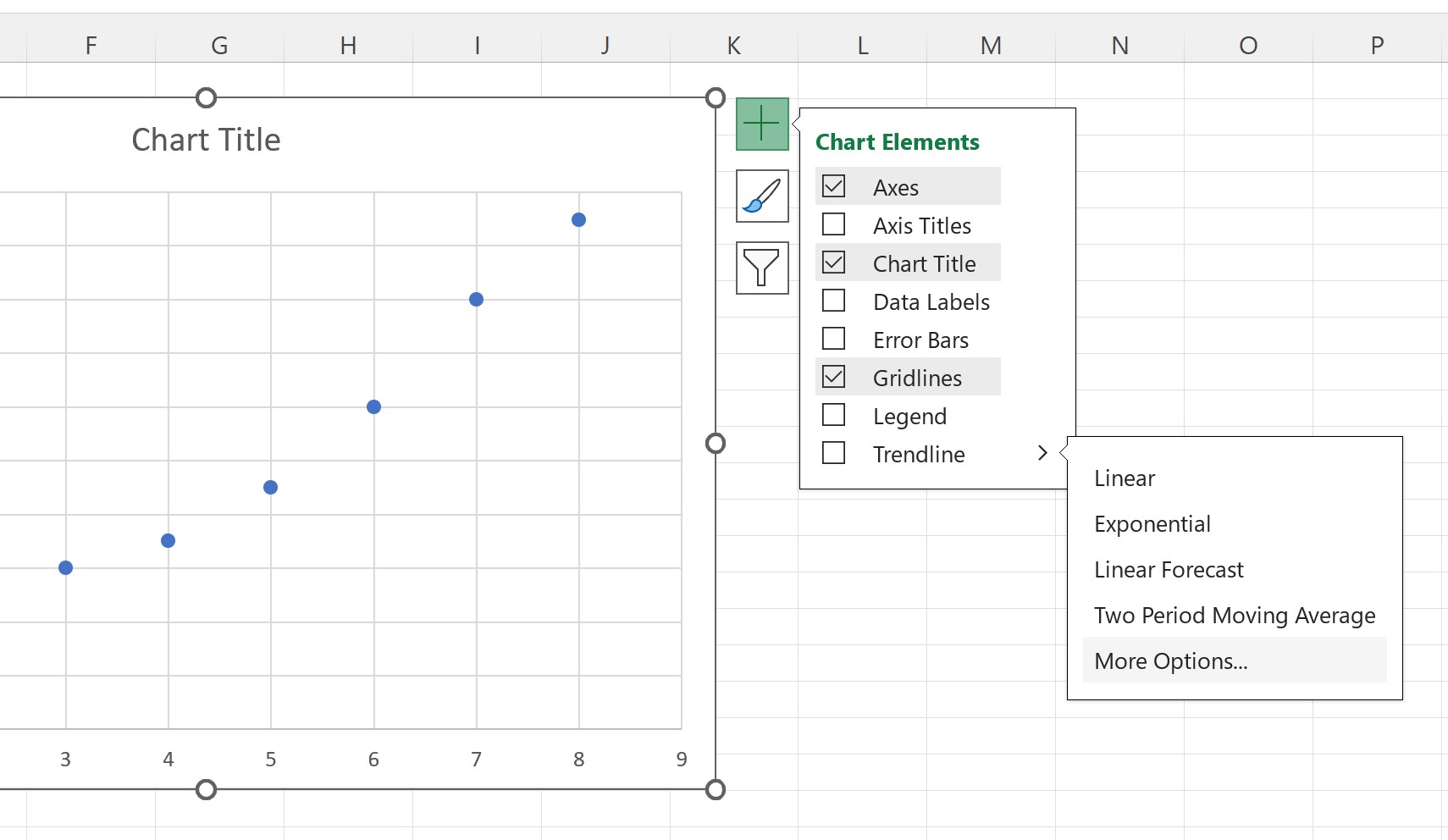
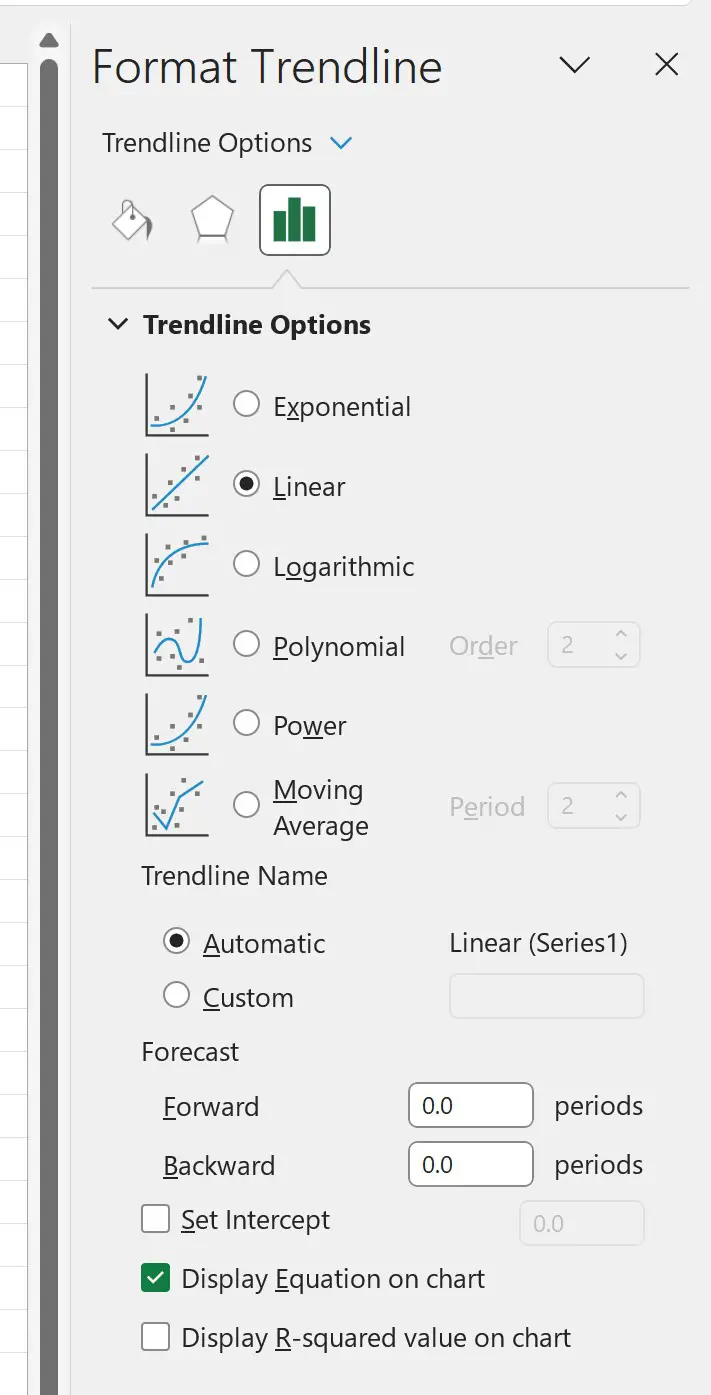
На появившейся панели «Формат линии тренда» нажмите кнопку рядом с параметром « Линейный как линия тренда», а затем установите флажок «Показать уравнение на диаграмме »:
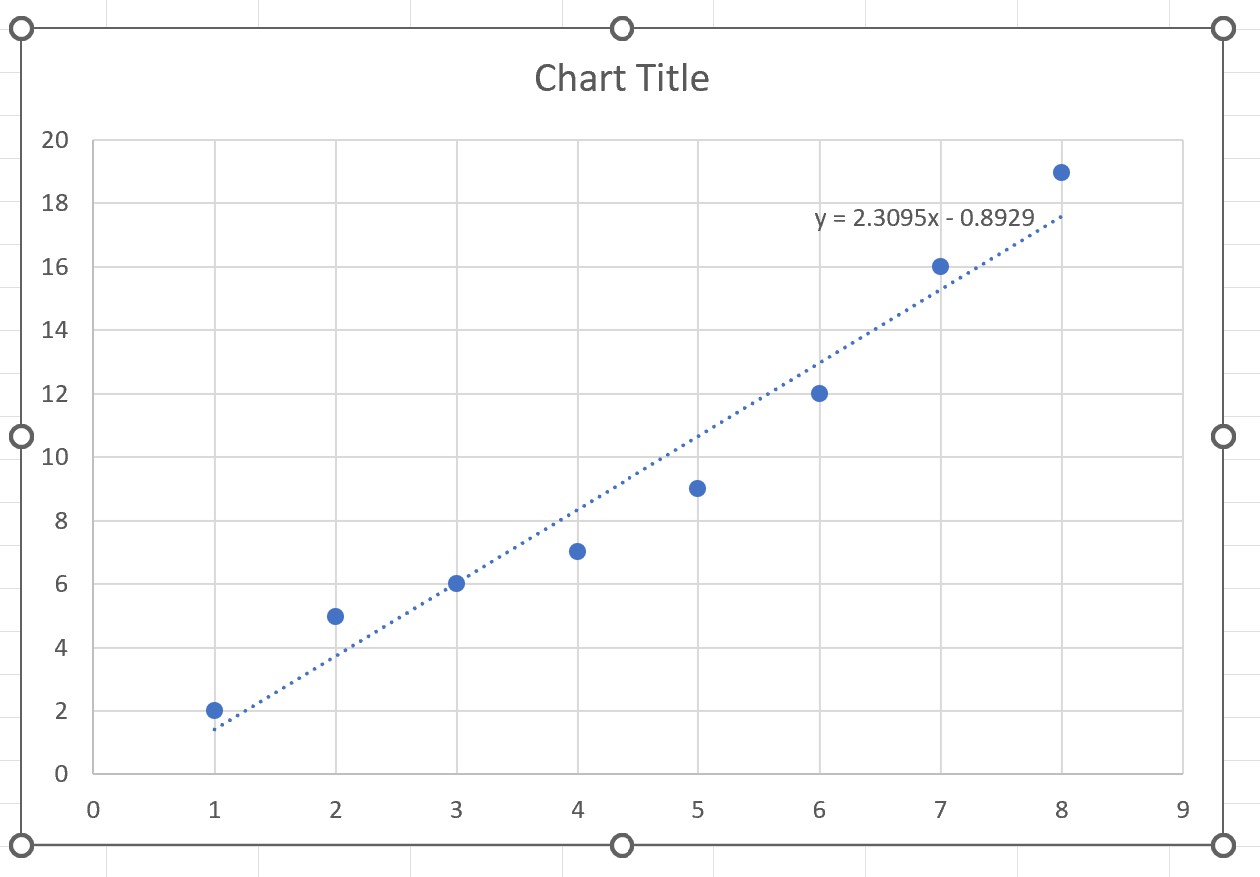
На графике появятся наиболее подходящая линия и ее уравнение:
Шаг 4: Интерпретируйте линию наилучшего соответствия
Из графика мы видим, что линия наилучшего соответствия имеет следующее уравнение:
у = 2,3095x – 0,8929
Вот как интерпретировать это уравнение:
- За каждый дополнительный час занятий среднее количество набранных баллов увеличивается на 2,3095 .
- Для игрока, который тренируется ноль часов, среднее количество набранных очков должно составлять -0,8929 .
Обратите внимание, что не всегда имеет смысл интерпретировать исходное значение в уравнении регрессии.
Например, игрок не может набрать отрицательные очки.
В этом конкретном примере нас в первую очередь интересует значение наклона линии регрессии, которое составляет 2,3095 .
Дополнительные ресурсы
В следующих руководствах объясняется, как выполнять другие распространенные задачи в Excel:
Как выполнить простую линейную регрессию в Excel
Как выполнить множественную линейную регрессию в Excel
Как посчитать R-квадрат в Excel