Полный код Python, используемый в этом уроке, можно найти здесь .
Как выполнить логистическую регрессию в python (шаг за шагом)
Логистическая регрессия — это метод, который мы можем использовать для подбора модели регрессии, когда переменная ответа является двоичной.
Логистическая регрессия использует метод, известный как оценка максимального правдоподобия , для нахождения уравнения следующей формы:
log[p(X) / ( 1 -p(X))] = β 0 + β 1 X 1 + β 2 X 2 + … + β p
Золото:
- X j : j- я прогнозируемая переменная
- β j : оценка коэффициента для j -й прогнозируемой переменной
Формула в правой части уравнения предсказывает логарифмическую вероятность того, что переменная ответа примет значение 1.
Итак, когда мы подгоняем модель логистической регрессии, мы можем использовать следующее уравнение для расчета вероятности того, что данное наблюдение примет значение 1:
p(X) = e β 0 + β 1 X 1 + β 2 X 2 + … + β p
Затем мы используем определенный порог вероятности, чтобы классифицировать наблюдение как 1 или 0.
Например, мы могли бы сказать, что наблюдения с вероятностью, большей или равной 0,5, будут классифицированы как «1», а все остальные наблюдения будут классифицированы как «0».
В этом руководстве представлен пошаговый пример выполнения логистической регрессии в R.
Шаг 1. Импортируйте необходимые пакеты.
Сначала мы импортируем необходимые пакеты для выполнения логистической регрессии в Python:
import pandas as pd import numpy as np from sklearn. model_selection import train_test_split from sklearn. linear_model import LogisticRegression from sklearn import metrics import matplotlib. pyplot as plt
Шаг 2. Загрузите данные
В этом примере мы будем использовать набор данных по умолчанию из книги «Введение в статистическое обучение» . Мы можем использовать следующий код для загрузки и отображения сводки набора данных:
#import dataset from CSV file on Github url = "https://raw.githubusercontent.com/Statorials/Python-Guides/main/default.csv" data = pd. read_csv (url) #view first six rows of dataset data[0:6] default student balance income 0 0 0 729.526495 44361.625074 1 0 1 817.180407 12106.134700 2 0 0 1073.549164 31767.138947 3 0 0 529.250605 35704.493935 4 0 0 785.655883 38463.495879 5 0 1 919.588530 7491.558572 #find total observations in dataset len( data.index ) 10000
Этот набор данных содержит следующую информацию о 10 000 человек:
- по умолчанию: указывает, совершил ли человек дефолт или нет.
- студент: указывает, является ли человек студентом или нет.
- баланс: средний баланс, который несет физическое лицо.
- доход: Доход физического лица.
Мы будем использовать статус студента, банковский баланс и доход, чтобы построить модель логистической регрессии, которая прогнозирует вероятность того, что данный человек объявит дефолт.
Шаг 3. Создайте образцы для обучения и тестирования.
Далее мы разделим набор данных на обучающий набор для обучения модели и тестовый набор для тестирования модели.
#define the predictor variables and the response variable X = data[[' student ',' balance ',' income ']] y = data[' default '] #split the dataset into training (70%) and testing (30%) sets X_train,X_test,y_train,y_test = train_test_split (X,y,test_size=0.3,random_state=0)
Шаг 4. Подберите модель логистической регрессии
Далее мы будем использовать функцию LogisticRegrade() , чтобы подогнать модель логистической регрессии к набору данных:
#instantiate the model log_regression = LogisticRegression() #fit the model using the training data log_regression. fit (X_train,y_train) #use model to make predictions on test data y_pred = log_regression. predict (X_test)
Шаг 5: Диагностика модели
После того, как мы подогнали модель регрессии, мы можем проанализировать эффективность нашей модели на тестовом наборе данных.
Сначала мы создадим матрицу путаницы для модели:
cnf_matrix = metrics. confusion_matrix (y_test, y_pred)
cnf_matrix
array([[2886, 1],
[113,0]])
Из матрицы путаницы мы видим, что:
- #Истинно положительные предсказания: 2886
- #Истинно отрицательные прогнозы: 0
- #Ложноположительные прогнозы: 113
- #Ложноотрицательные прогнозы: 1
Мы также можем получить модель точности, которая сообщает нам процент корректировок, сделанных моделью:
print(" Accuracy: ", metrics.accuracy_score (y_test, y_pred))l
Accuracy: 0.962
Это говорит нам о том, что модель сделала правильный прогноз о том, объявит ли человек дефолт в 96,2% случаев.
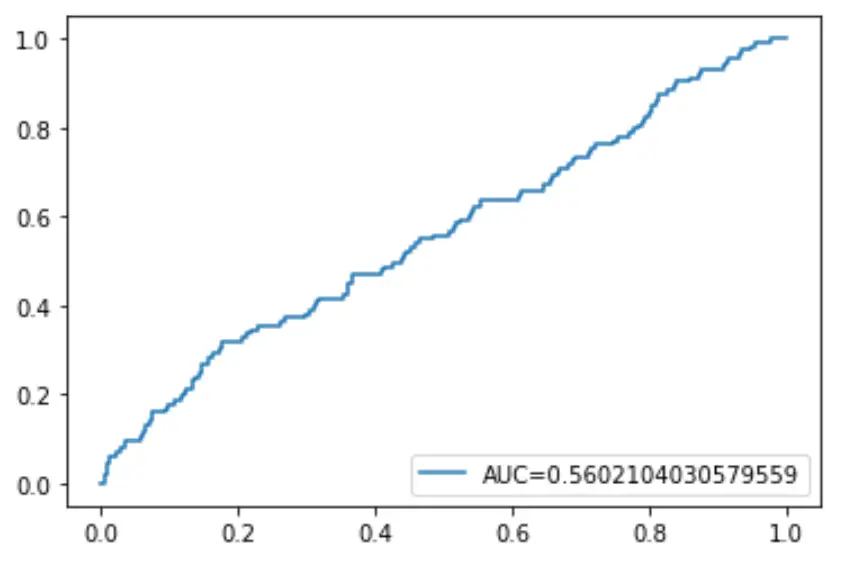
Наконец, мы можем построить кривую рабочих характеристик приемника (ROC), которая отображает процент истинных положительных результатов, предсказанных моделью, когда порог вероятности прогнозирования снижается с 1 до 0.
Чем выше AUC (площадь под кривой), тем точнее наша модель способна предсказать результаты:
#define metrics
y_pred_proba = log_regression. predict_proba (X_test)[::,1]
fpr, tpr, _ = metrics. roc_curve (y_test, y_pred_proba)
auc = metrics. roc_auc_score (y_test, y_pred_proba)
#create ROC curve
plt. plot (fpr,tpr,label=" AUC= "+str(auc))
plt. legend (loc=4)
plt. show ()