Как выполнить логистическую регрессию в spss
Логистическая регрессия — это метод, который мы используем для подбора модели регрессии , когда переменная ответа является двоичной.
В этом руководстве объясняется, как выполнить логистическую регрессию в SPSS.
Пример: логистическая регрессия в SPSS
Используйте следующие шаги, чтобы выполнить логистическую регрессию в SPSS для набора данных, показывающего, были ли баскетболисты колледжей призваны в НБА (драфт: 0 = нет, 1 = да) на основе их среднего балла. очков за игру и уровень их дивизиона.
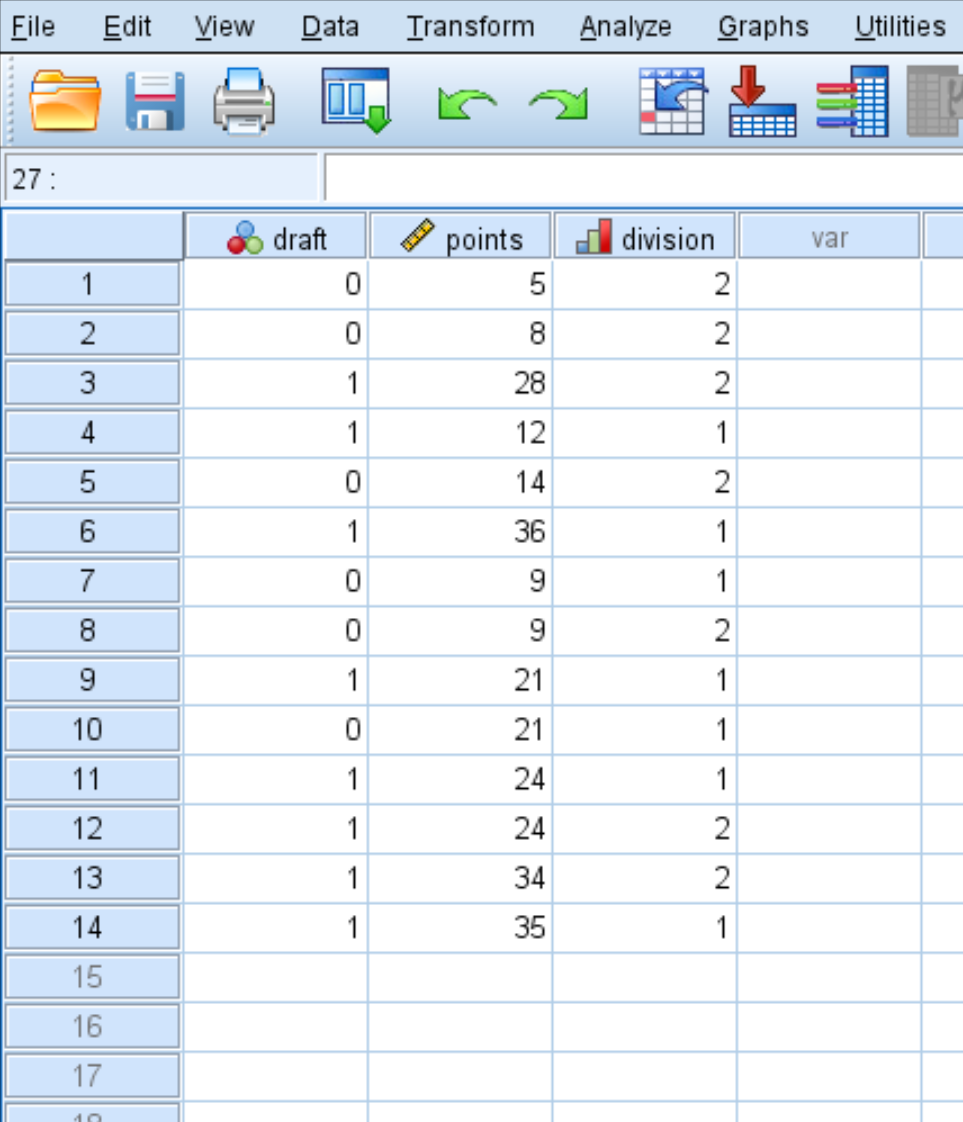
Шаг 1: Введите данные.
Сначала введите следующие данные:
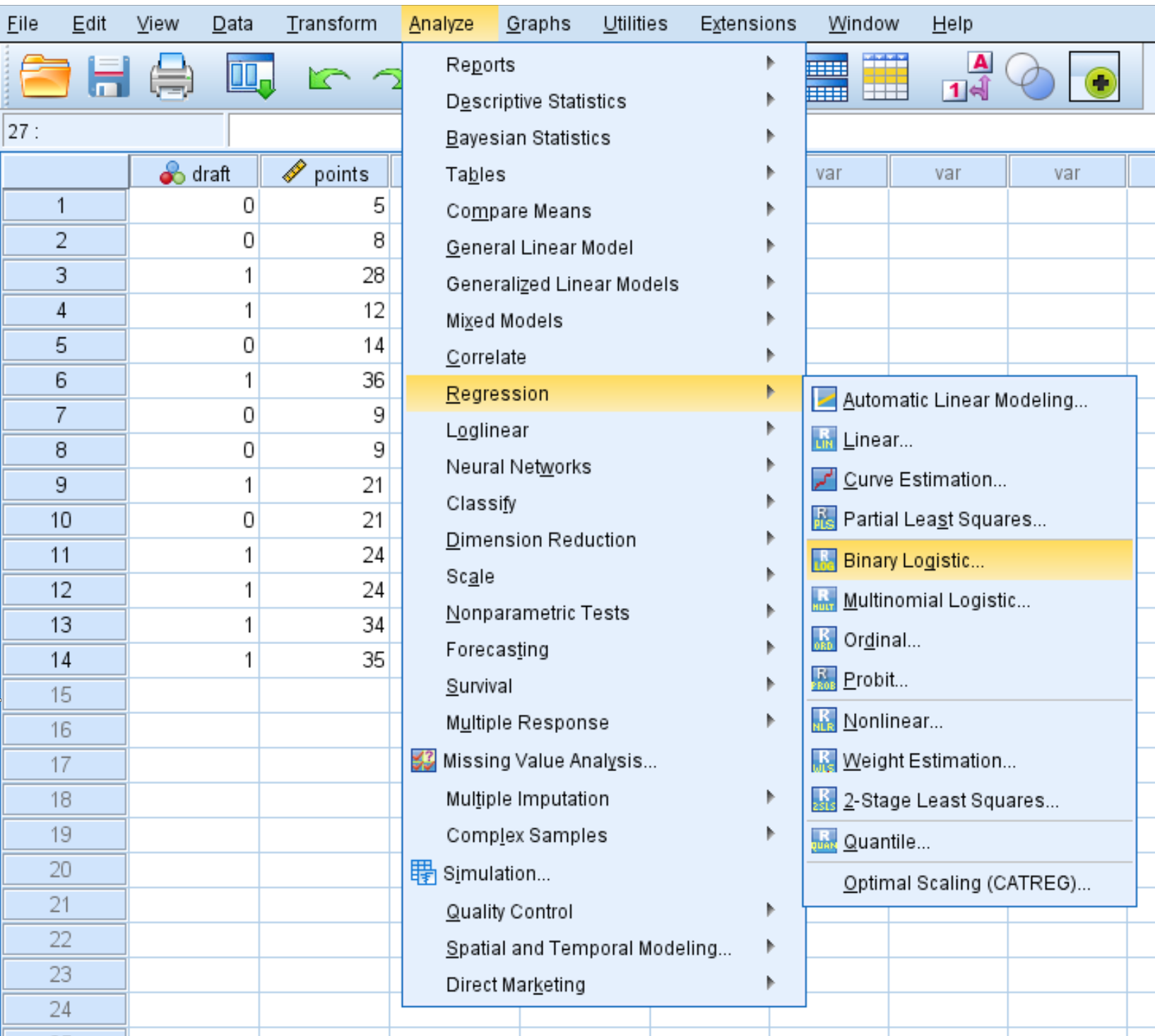
Шаг 2: Выполните логистическую регрессию.
Перейдите на вкладку «Анализ» , затем «Регрессия» , затем «Двоичная логистическая регрессия» :
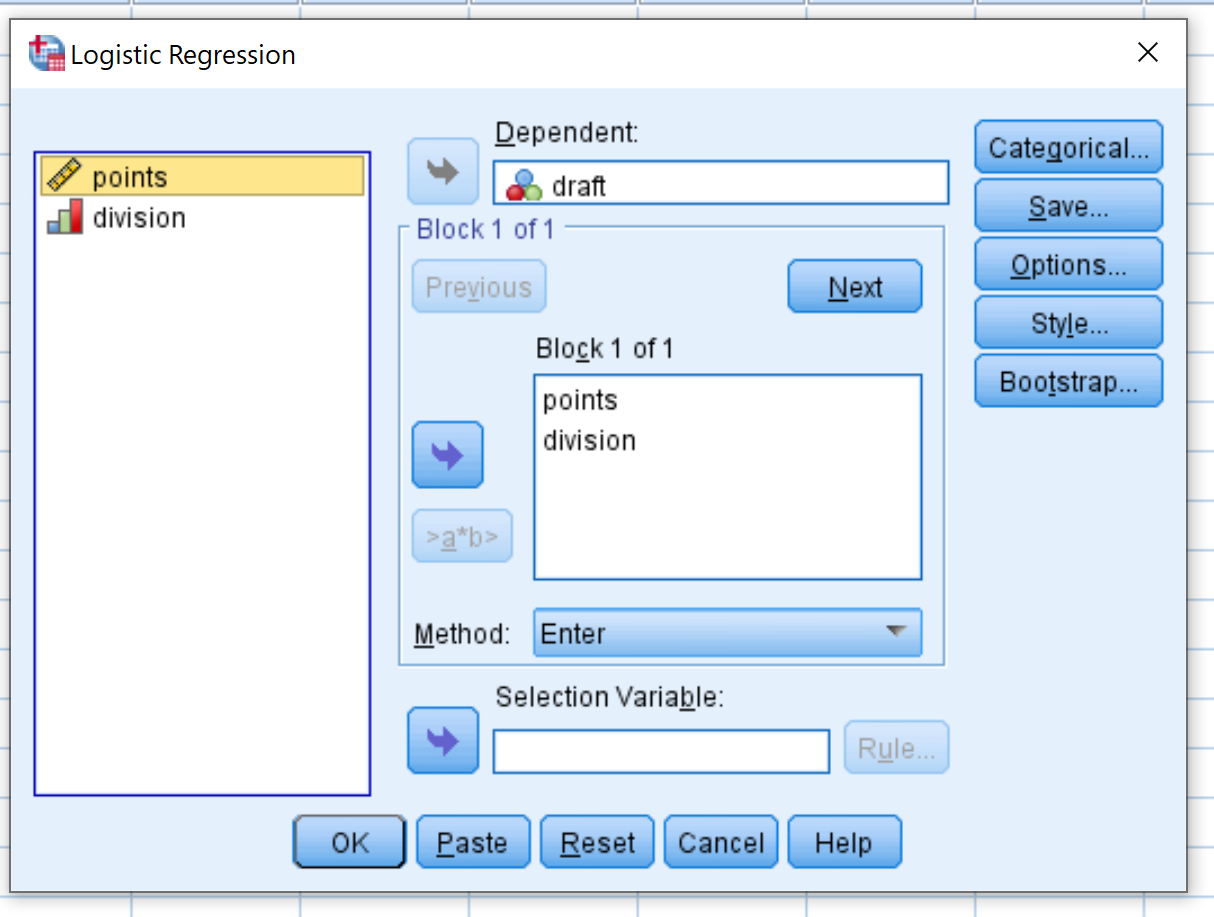
В появившемся новом окне перетащите проект переменной двоичного ответа в область с надписью Зависимая. Затем перетащите двоеточие и деление переменных-предикторов в поле с надписью «Блок 1 из 1». Оставьте для метода значение Enter. Затем нажмите ОК .
Шаг 3. Интерпретируйте результат.
Как только вы нажмете «ОК» , появится результат логистической регрессии:
Вот как интерпретировать результат:
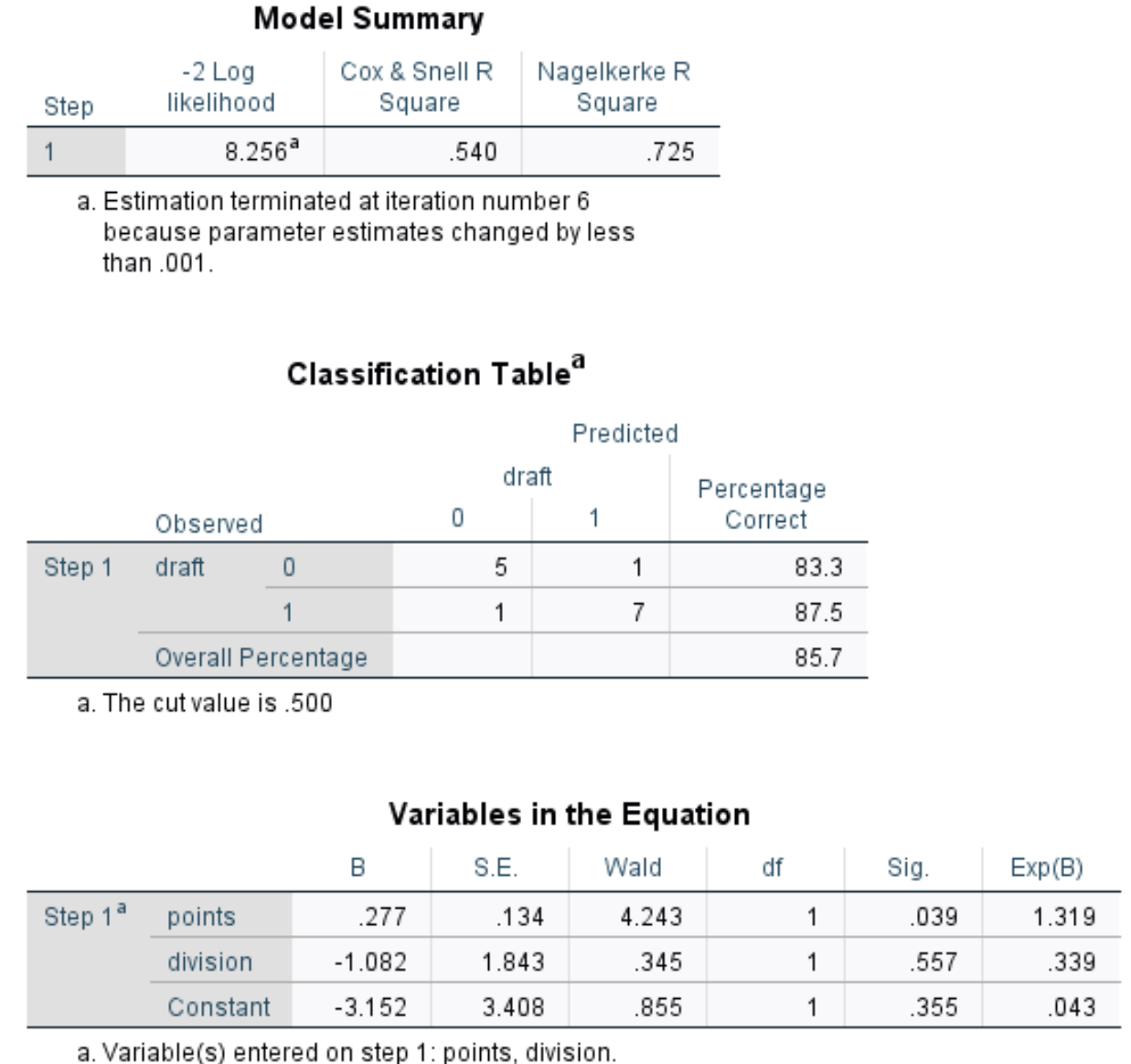
Краткое описание модели: Наиболее полезным показателем в этой таблице является R-квадрат Нагелькерке, который сообщает нам процент вариаций переменной отклика , который можно объяснить переменными-предикторами. В этом случае баллы и деление могут объяснить 72,5% изменчивости осадки.
Таблица классификации. Наиболее полезным показателем в этой таблице является общий процент, который сообщает нам процент наблюдений, которые модель смогла правильно классифицировать. В этом случае модель логистической регрессии смогла правильно предсказать исход драфта 85,7% игроков.
Переменные в уравнении. Последняя таблица дает нам несколько полезных измерений, в том числе:
- Уолд: статистика теста Уолда для каждой предикторной переменной, которая используется для определения того, является ли каждая предикторная переменная статистически значимой или нет.
- Sig: значение p, соответствующее статистике теста Вальда для каждой предикторной переменной. Мы видим, что значение p для точек составляет 0,039, а значение p для деления — 0,557.
- Exp(B): отношение шансов для каждой предикторной переменной. Это говорит нам об изменении шансов на выбор игрока, связанном с увеличением на одну единицу данной предикторной переменной. Например, шансы на то, что игрок Дивизиона 2 будет выбран на драфте, составляют всего 0,339 от шансов на то, что игрок Дивизиона 1 будет выбран. Аналогично, каждое дополнительное увеличение количества очков за игру связано с увеличением на 1319 шансов на то, что игрок будет выбран на драфте.
Затем мы можем использовать коэффициенты (значения в столбце с надписью B), чтобы предсказать вероятность того, что данный игрок будет выбран на драфте, используя следующую формулу:
Вероятность = e -3,152 + 0,277 (баллов) – 1,082 (деление) / (1+e -3,152 + 0,277 (баллов) – 1,082 (деление) )
Например, вероятность того, что игрок, набирающий в среднем 20 очков за игру и играющий в Дивизионе 1, будет выбран на драфте, можно рассчитать следующим образом:
Вероятность = e -3,152 + 0,277(20) – 1,082(1) / (1+e -3,152 + 0,277(20) – 1,082(1) ) = 0,787 .
Поскольку эта вероятность больше 0,5, мы прогнозируем, что этот игрок будет выбран на драфте.
Шаг 4. Сообщите о результатах.
Наконец, мы хотели бы сообщить о результатах нашей логистической регрессии. Вот пример того, как это сделать:
Была проведена логистическая регрессия, чтобы определить, как очки за игру и уровень дивизиона влияют на вероятность того, что баскетболист будет выбран на драфте. Всего в анализе было задействовано 14 игроков.
Модель объяснила 72,5% вариаций результатов проекта и правильно классифицировала 85,7% случаев.
Шансы на то, что игрок Дивизиона 2 будет выбран на драфте, составляли всего 0,339 от шансов на то, что игрок Дивизиона 1 будет выбран.
Каждая дополнительная единица увеличения количества очков за игру была связана с увеличением на 1319 шансов на то, что игрок будет выбран на драфте.