Как выполнить логистическую регрессию в sas

Логистическая регрессия — это метод, который мы можем использовать для подбора модели регрессии, когда переменная ответа является двоичной.

Логистическая регрессия использует метод, известный как оценка максимального правдоподобия , для нахождения уравнения следующей формы:

log[p(X)/(1 _— p(X))] = β ₀ + β ₁ X ₁ + β ₂ X ₂ + … + β _p

Золото:

• X _j : j- ^я прогнозируемая переменная
• β _j : оценка коэффициента для j ^-й прогнозируемой переменной

Формула в правой части уравнения предсказывает логарифмическую вероятность того, что переменная ответа примет значение 1.

В следующем пошаговом примере показано, как реализовать модель логистической регрессии в SAS.

Шаг 1. Создайте набор данных

Сначала мы создадим набор данных, содержащий информацию о следующих трех переменных для 18 студентов:

• Прием в определенный колледж (1 = да, 0 = нет)
• Средний балл (шкала от 1 до 4)
• Оценка ACT (шкала от 1 до 36)

 /*create dataset*/
data my_data;
    input acceptance gpa act;
    datalines ;
1 3 30
0 1 21
0 2 26
0 1 24
1 3 29
1 3 34
0 3 31
1 2 29
0 1 21
1 2 21
0 1 15
1 3 32
1 4 31
1 4 29
0 1 24
1 4 29
1 3 21
1 4 34
;
run ;

/*view dataset*/
proc print data =my_data;

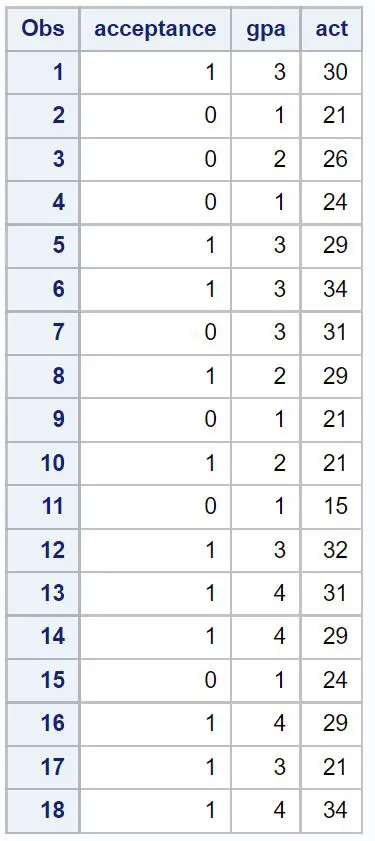
Шаг 2. Подберите модель логистической регрессии

Далее мы будем использовать логистику процессов , чтобы соответствовать модели логистической регрессии, используя «принятие» в качестве переменной ответа, а «gpa» и «действие» в качестве переменных-предсказателей.

Примечание . Чтобы SAS прогнозировал вероятность того, что переменная ответа примет значение 1, необходимо указать уменьшение . По умолчанию SAS прогнозирует вероятность того, что переменная ответа примет значение 0.

 /*fit logistic regression model*/
proc logistic data =my_data descending ;
  model acceptance = gpa act;
run ;

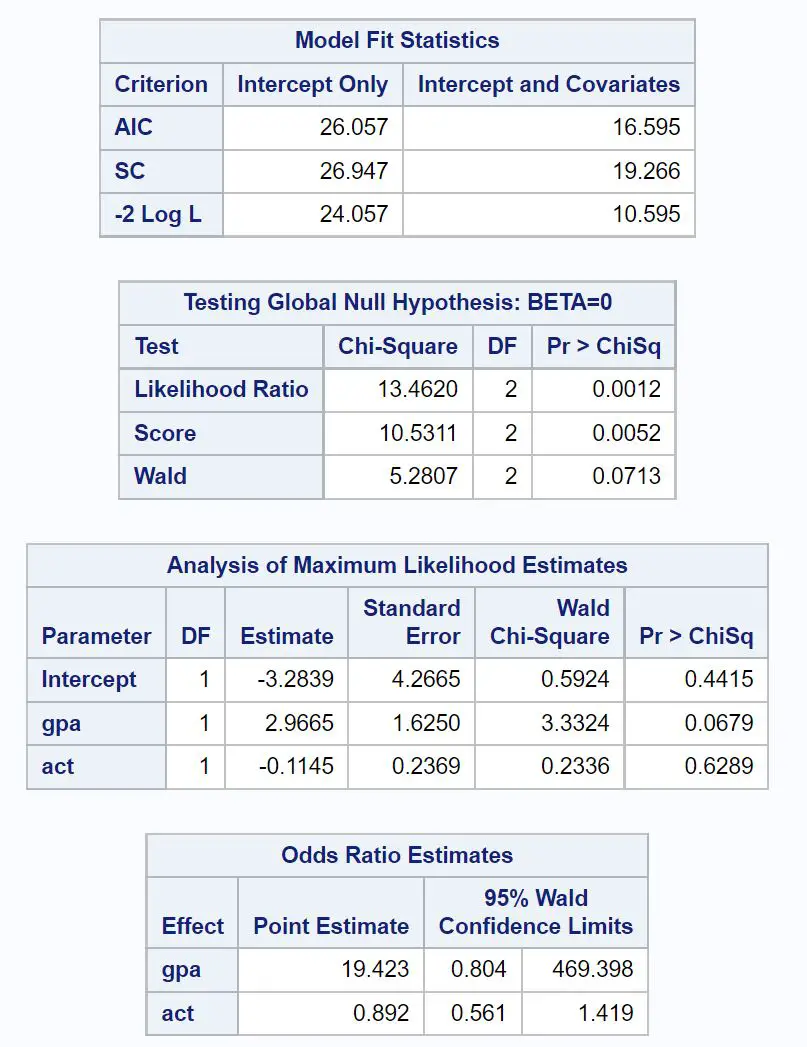
Первая интересующая таблица называется «Статистика соответствия модели» .

Из этой таблицы мы видим значение AIC модели, которое оказывается равным 16,595 . Чем ниже значение AIC, тем лучше модель соответствует данным.

Однако не существует порога того, что считается «хорошим» значением AIC . Скорее, мы используем AIC для сравнения соответствия нескольких моделей одному и тому же набору данных. Модель с наименьшим значением AIC обычно считается лучшей.

Следующая интересная таблица называется «Проверка глобальной нулевой гипотезы: BETA=0 ».

Из этой таблицы мы можем видеть значение хи-квадрат отношения правдоподобия 13,4620 с соответствующим значением p 0,0012 .

Поскольку это значение p меньше 0,05, это говорит нам о том, что модель логистической регрессии в целом статистически значима.

Далее мы можем проанализировать оценки коэффициентов в таблице под названием «Анализ оценок максимального правдоподобия» .

Из этой таблицы мы можем увидеть коэффициенты для среднего балла и действия, которые указывают среднее изменение логарифмических шансов быть принятым в колледж при увеличении на одну единицу каждой переменной.

Например:

• Увеличение среднего балла на одну единицу связано со средним увеличением на 2,9665 логарифмических шансов быть принятым в колледж.
• Увеличение балла ACT на одну единицу связано со средним снижением на 0,1145 логарифмических шансов быть принятым в колледж.

Соответствующие значения p в результате также дают нам представление о том, насколько эффективна каждая переменная-предиктор в прогнозировании вероятности ее принятия:

• GPA P-значение: 0,0679
• Значение ACT P: 0,6289

Это говорит нам о том, что средний балл является статистически значимым предиктором поступления в колледж, в то время как балл ACT не является статистически значимым.

Дополнительные ресурсы

В следующих руководствах объясняется, как адаптировать другие модели регрессии в SAS:

Как выполнить простую линейную регрессию в SAS
Как выполнить множественную линейную регрессию в SAS