U-тест манна-уитни
U-критерий Манна-Уитни (иногда называемый критерием суммы рангов Уилкоксона) используется для сравнения различий между двумя независимыми выборками, когда распределения выборок не имеют нормального распределения и размеры выборки малы (n < 30).
Он считается непараметрическим эквивалентом независимого двухвыборочного t-критерия .
Вот несколько примеров того, когда вы можете использовать U-тест Манна-Уитни:
- Вы хотите сравнить зарплаты пяти выпускников университета А с зарплатами пяти выпускников университета Б. Зарплаты обычно не распределяются.
- Вы хотите знать, различается ли потеря веса для двух групп: 12 человек, использующих диету А, и 10 человек, использующих диету Б. Потеря веса обычно не распределяется.
- Вы хотите знать, отличаются ли оценки 8 учеников класса А от оценок 7 учеников класса Б. Обычно баллы не распределяются.
В каждом примере вы хотите сравнить две группы, распределение выборки не является нормальным, а размеры выборки малы.
Таким образом, U-критерий Манна-Уитни подходит, если выполняются следующие предположения.
Допущения U-теста Манна-Уитни
Прежде чем выполнять U-тест Манна-Уитни, вы должны убедиться, что выполняются следующие четыре предположения:
- Обычный или непрерывный: переменная, которую вы анализируете, является порядковой или непрерывной. Примеры порядковых переменных включают пункты Лайкерта (например, 5-балльная шкала от «полностью не согласен» до «полностью согласен»). Примеры непрерывных переменных включают рост (измеряется в дюймах), вес (измеряется в фунтах) или результаты тестов (измеряются от 0 до 100).
- Независимость: Все наблюдения обеих групп независимы друг от друга.
- Форма: Формы распределений для двух групп примерно одинаковы.
Если эти предположения выполняются, вы можете выполнить U-тест Манна-Уитни.
Как выполнить U-тест Манна-Уитни
Чтобы выполнить U-тест Манна-Уитни, мы следуем стандартной пятиэтапной процедуре проверки гипотез :
1. Сформулируйте предположения.
В большинстве случаев U-критерий Манна-Уитни выполняется как двусторонний тест. Нулевая и альтернативная гипотезы записываются в виде:
H 0 : Обе популяции равны.
Ха : Эти две популяции не равны.
2. Определите уровень значимости гипотезы.
Определитесь с уровнем значимости. Обычно выбираются значения .01, .05 и .1.
3. Найдите статистику теста.
Статистика теста обозначается U и является меньшей из U 1 и U 2 , как определено ниже:
U 1 = n 1 n 2 + n 1 (n 1 +1)/2 – R 1
U 2 = n 1 n 2 + n 2 (n 2 +1)/2 – R 2
где n 1 и n 2 — размеры выборки для выборок 1 и 2 соответственно, а R 1 и R 2 — сумма рангов для выборок 1 и 2 соответственно.
В приведенных ниже примерах показано, как подробно найти эту статистику теста.
4. Отклонить или не отвергать нулевую гипотезу.
Используя статистику теста, определите, можете ли вы отвергнуть нулевую гипотезу на основе уровня значимости и критического значения, найденных в U-таблице Манна-Уитни.
5. Интерпретируйте результаты.
Интерпретируйте результаты теста в контексте заданного вопроса.
Примеры проведения U-теста Манна-Уитни
Следующие примеры показывают, как выполнить U-тест Манна-Уитни.
Пример 1
Мы хотим знать, эффективно ли новое лекарство для предотвращения приступов паники. Всего 12 пациентов случайным образом были разделены на две группы по 6 человек и назначены для приема нового препарата или плацебо. Затем пациенты записывают количество приступов паники, которые они испытали в течение месяца.
Результаты показаны ниже:
| НОВЫЙ ПРЕПАРАТ | ПЛАЦЕБО |
|---|---|
| 3 | 4 |
| 5 | 8 |
| 1 | 6 |
| 4 | 2 |
| 3 | 1 |
| 5 | 9 |
Проведите U-тест Манна-Уитни, чтобы увидеть, есть ли разница в количестве приступов паники среди пациентов в группе плацебо по сравнению с группой, принимавшей новый препарат. Используйте уровень значимости 0,05.
1. Сформулируйте предположения.
H 0 : Обе популяции равны.
Ха : Эти две популяции не равны.
2. Определите уровень значимости гипотезы.
Задача подсказывает нам, что нам следует использовать уровень значимости 0,05.
3. Найдите статистику теста.
Напомним, что тестовая статистика обозначается U и является меньшей из U 1 и U 2 , как определено ниже:
U 1 = n 1 n 2 + n 1 (n 1 +1)/2 – R 1
U 2 = n 1 n 2 + n 2 (n 2 +1)/2 – R 2
где n 1 и n 2 — размеры выборки для выборок 1 и 2 соответственно, а R 1 и R 2 — сумма рангов для выборок 1 и 2 соответственно.
Чтобы найти R 1 и R 2 , нам нужно объединить наблюдения обеих групп и упорядочить их от меньшего к большему:
| НОВЫЙ ПРЕПАРАТ | ПЛАЦЕБО |
|---|---|
| 3 | 4 |
| 5 | 8 |
| 1 | 6 |
| 4 | 2 |
| 3 | 1 |
| 5 | 9 |
Всего выборка: 1 , 1 , 2 , 3 , 3 , 4 , 4 , 5 , 5 , 6 , 8 , 9
Ранги: 1.5 , 1.5 , 3 , 4.5 , 4.5 , 6.5 , 6.5 , 8.5 , 8.5 , 10 , 11 , 12.
R 1 = сумма рангов выборки 1 = 1,5+4,5+4,5+6,5+8,5+8,5 = 34
R 2 = сумма рангов выборки 2 = 1,5+3+6,5+10+11+12 = 44
Далее мы используем размеры выборки n 1 и n 2 , а также нашу сумму рангов R 1 и R 2 , чтобы найти U 1 и U 2 .
U1 = 6(6) + 6(6+1)/2 – 34 = 23
U2 = 6(6) + 6(6+1)/2 – 44 = 13
Наша тестовая статистика — это меньшая из U1 и U2 , которая равна U=13.
Примечание. Мы также могли бы использовать калькулятор U-критерия Манна-Уитни , чтобы определить, что U = 13.
4. Отклонить или не отвергать нулевую гипотезу.
Используя n 1 = 6 и n 2 = 6 с уровнем значимости 0,05, U-таблица Манна-Уитни сообщает нам, что критическое значение равно 5:
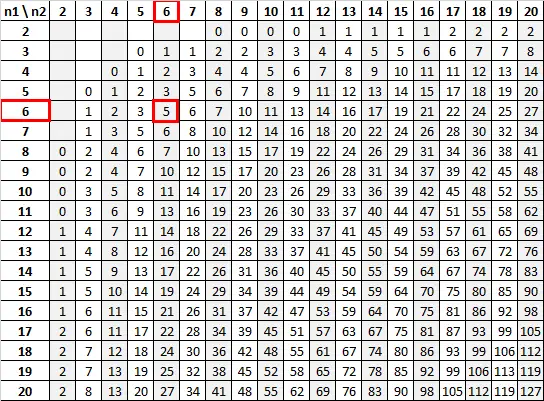
Поскольку наша тестовая статистика (13) больше нашего критического значения (5), мы не можем отвергнуть нулевую гипотезу.
5. Интерпретируйте результаты.
Поскольку нам не удалось отвергнуть нулевую гипотезу, у нас нет достаточных доказательств, чтобы сказать, что количество приступов паники, которые испытывают пациенты в группе плацебо, отличается от такового в группе нового препарата.
Пример 2
Мы хотим знать, помогает ли изучение 30 минут в день в течение недели учащимся лучше на экзамене. Всего 15 пациентов случайным образом распределяются в группу исследования или в группу без исследования. Через неделю все ученики сдают один и тот же тест.
Результаты испытаний для обеих групп показаны ниже:
| ИЗУЧАТЬ | НЕТ ИССЛЕДОВАНИЯ |
|---|---|
| 89 | 88 |
| 92 | 93 |
| 94 | 95 |
| 96 | 75 |
| 91 | 72 |
| 99 | 80 |
| 84 | 81 |
| 90 |
Выполните U-тест Манна-Уитни, чтобы увидеть, есть ли разница в результатах тестов для исследуемой группы по сравнению с группой, не участвовавшей в исследовании. Используйте уровень значимости 0,01.
1. Сформулируйте предположения.
H 0 : Обе популяции равны.
Ха : Эти две популяции не равны.
2. Определите уровень значимости гипотезы.
Задача подсказывает нам, что нам следует использовать уровень значимости 0,01.
3. Найдите статистику теста.
Напомним, что тестовая статистика обозначается U и является меньшей из U 1 и U 2 , как определено ниже:
U 1 = n 1 n 2 + n 1 (n 1 +1)/2 – R 1
U 2 = n 1 n 2 + n 2 (n 2 +1)/2 – R 2
где n 1 и n 2 — размеры выборки для выборок 1 и 2 соответственно, а R 1 и R 2 — сумма рангов для выборок 1 и 2 соответственно.
Чтобы найти R 1 и R 2 , нам нужно объединить наблюдения обеих групп и упорядочить их от меньшего к большему:
| ИЗУЧАТЬ | НЕТ ИССЛЕДОВАНИЯ |
|---|---|
| 89 | 88 |
| 92 | 93 |
| 94 | 95 |
| 96 | 75 |
| 91 | 72 |
| 99 | 80 |
| 84 | 81 |
| 90 |
Всего выборка: 72 , 75 , 80 , 81, 84, 88 , 89 , 90 , 91 , 92 , 93 , 94 , 95 , 96 , 99.
Ряды: 1 , 2 , 3 , 4 , 5 , 6 , 7 , 8 , 9 , 10 , 11 , 12 , 13 , 14 , 15.
R 1 = сумма рангов выборки 1 = 5+7+8+9+10+12+14+15 = 80
R 2 = сумма рангов выборки 2 = 1+2+3+4+6+11+13 = 40
Далее мы используем размеры выборки n 1 и n 2 , а также нашу сумму рангов R 1 и R 2 , чтобы найти U 1 и U 2 .
U1 = 8(7) + 8(8+1)/2 – 80 = 12
U2 = 8(7) + 7(7+1)/2 – 40 = 44
Наша тестовая статистика — это меньшая из U1 и U2 , которая равна U=12.
Примечание. Мы также могли бы использовать калькулятор U-критерия Манна-Уитни , чтобы определить, что U = 12.
4. Отклонить или не отвергать нулевую гипотезу.
Используя n 1 = 8 и n 2 = 7 с уровнем значимости 0,01, U-таблица Манна-Уитни сообщает нам, что критическое значение равно 6:
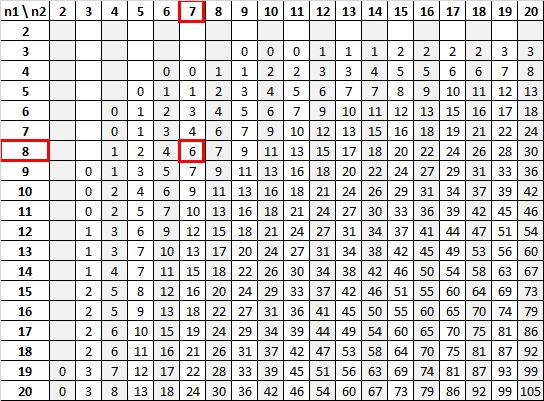
Поскольку наша тестовая статистика (12) больше нашего критического значения (6), мы не можем отвергнуть нулевую гипотезу.
5. Интерпретируйте результаты.
Поскольку нам не удалось отвергнуть нулевую гипотезу, у нас нет достаточных доказательств, чтобы сказать, что результаты тестов студентов, которые учились, отличаются от результатов тестов студентов, которые не учились.
Дополнительные ресурсы
Калькулятор U-теста Манна-Уитни
U-стол Манна-Уитни
Как выполнить U-тест Манна-Уитни в Excel
Как выполнить U-тест Манна-Уитни в R
Как выполнить U-тест Манна-Уитни на Python
Как выполнить U-тест Манна-Уитни в SPSS
Как выполнить U-тест Манна-Уитни в Stata
Об авторе
бенджамин андерсон
Здравствуйте, я Бенджамин, профессор статистики на пенсии, ставший преданным преподавателем Statorials. Имея обширный опыт и знания в области статистики, я хочу поделиться своими знаниями, чтобы расширить возможности студентов с помощью Statorials. Узнать больше