Полное руководство: как проверить предположения manova

MANOVA (многомерный дисперсионный анализ) используется для анализа того, как одна или несколько факторных переменных влияют на несколько переменных ответа.

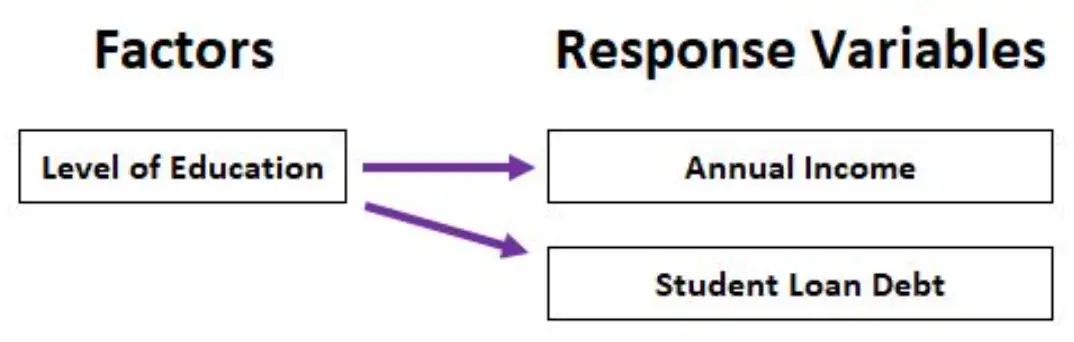
Например, мы могли бы использовать MANOVA для анализа того, как уровень образования (диплом средней школы, степень младшего специалиста, степень бакалавра, степень магистра) влияет как на годовой доход, так и на общую задолженность по студенческим кредитам.

Связанный: различия между ANOVA, ANCOVA, MANOVA и MANCOVA

Каждый раз, когда мы выполняем MANOVA, мы должны убедиться, что выполняются следующие предположения:

1. Многомерная нормальность . Переменные отклика имеют многомерное нормальное распределение внутри каждой группы факторных переменных.

2. Независимость . Каждое наблюдение случайным образом и независимо отбирается из генеральной совокупности.

3. Равная дисперсия . Ковариационные матрицы совокупности каждой группы равны.

4. Отсутствие многомерных выбросов . Экстремальных многомерных выбросов нет.

В этой статье мы даем объяснение каждому предположению, а также то, как определить, выполняется ли это предположение.

Предположение 1: Многомерная нормальность

MANOVA предполагает, что переменные отклика являются многомерными, нормально распределенными внутри каждой группы факторной переменной.

Если для каждой комбинации фактор * ответная переменная имеется не менее 20 наблюдений, то можно предположить, что предположение о многомерной нормальности выполнено.

Если для каждой комбинации фактор*ответная переменная имеется менее 20 наблюдений, мы можем создать матрицу диаграммы рассеяния для визуализации остатков и визуально проверить, выполняется ли это предположение.

К счастью, хорошо известно, что MANOVA устойчива к отклонениям от многомерной нормальности, поэтому отклонения от небольших до умеренных обычно не являются проблемой.

Гипотеза 2: Независимость

MANOVA предполагает, что каждое наблюдение случайным образом и независимо отбирается из генеральной совокупности.

Поскольку для сбора данных используется метод вероятностной выборки (каждый член совокупности имеет равную вероятность попасть в выборку), мы можем предположить, что каждое наблюдение было выбрано случайным и независимым образом.

Примеры методов вероятностной выборки включают в себя:

• Простая случайная выборка
• Стратифицированная случайная выборка
• Случайная кластерная выборка
• Систематическая случайная выборка

Предположение 3: равная дисперсия

MANOVA предполагает, что ковариационные матрицы совокупности каждой группы равны.

Самый распространенный способ проверить эту гипотезу — использовать М-критерий Бокса. Известно, что этот тест довольно строгий, поэтому мы обычно используем уровень значимости 0,001, чтобы определить, равны или нет ковариационные матрицы генеральной совокупности.

Если p-значение М-теста Бокса больше 0,001, мы можем предположить, что это предположение выполнено.

К счастью, даже если значение p теста меньше 0,001, MANOVA имеет тенденцию быть устойчивой к отклонениям от этой гипотезы.

Чтобы неравные ковариационные матрицы были проблемой, различия между ковариационными матрицами должны быть весьма значительными.

Гипотеза 4: отсутствие многомерных выбросов

MANOVA предполагает, что в данных нет экстремальных многомерных выбросов, которые могли бы существенно повлиять на результаты.

Самый распространенный способ проверить это предположение — вычислить расстояние Махаланобиса для каждого наблюдения, которое представляет собой расстояние между двумя точками в многомерном пространстве.

Если соответствующее значение p для расстояния Махаланобиса для наблюдения меньше 0,001, мы обычно объявляем это наблюдение крайним выбросом.

Обратитесь к следующим руководствам, чтобы узнать, как рассчитать расстояние Махаланобиса в различных статистических программах:

• Как рассчитать расстояние Махаланобиса в R
• Как рассчитать расстояние Махаланобиса в SPSS
• Как рассчитать расстояние Махаланобиса в Python

Дополнительные ресурсы

В следующих руководствах объясняется, как выполнить MANOVA в различных статистических программах:

Как выполнить MANOVA в R
Как выполнить MANOVA в SPSS
Как выполнить MANOVA в Stata