Как создать матрицу диаграммы рассеяния в r (2 примера)

Матрица диаграммы рассеяния — это матрица диаграммы рассеяния, которая позволяет понять попарные отношения между различными переменными в наборе данных.

Существует два распространенных способа создания матрицы диаграммы рассеяния в R:

Метод 1: используйте базу R

 #create scatterplot matrix (pch=20 means to use a solid circle for points)
plot(df, pch= 20 )

Способ 2: используйте пакеты ggplot2 и GGally.

 library (ggplot2)
library (GGally)

#create scatterplot matrix
ggpairs(df)

В следующих примерах показано, как использовать каждый метод на практике со следующим фреймом данных в R:

 #create data frame
df <- data. frame (points=c(99, 90, 86, 88, 95, 99, 101, 104),
                 assists=c(33, 28, 31, 39, 40, 40, 35, 47),
                 rebounds=c(30, 28, 24, 24, 20, 20, 15, 12))

#view first few rows of data frame
head(df)

  points assists rebounds
1 99 33 30
2 90 28 28
3 86 31 24
4 88 39 24
5 95 40 20
6 99 40 20

Пример 1. Создайте матрицу диаграммы рассеяния с использованием базы R

Мы можем использовать базовую функцию Rplot() для создания матрицы диаграммы рассеяния для каждой переменной в нашем фрейме данных:

 #create scatterplot matrix
plot(df, pch= 20 , cex= 1.5 , col=' steelblue ')

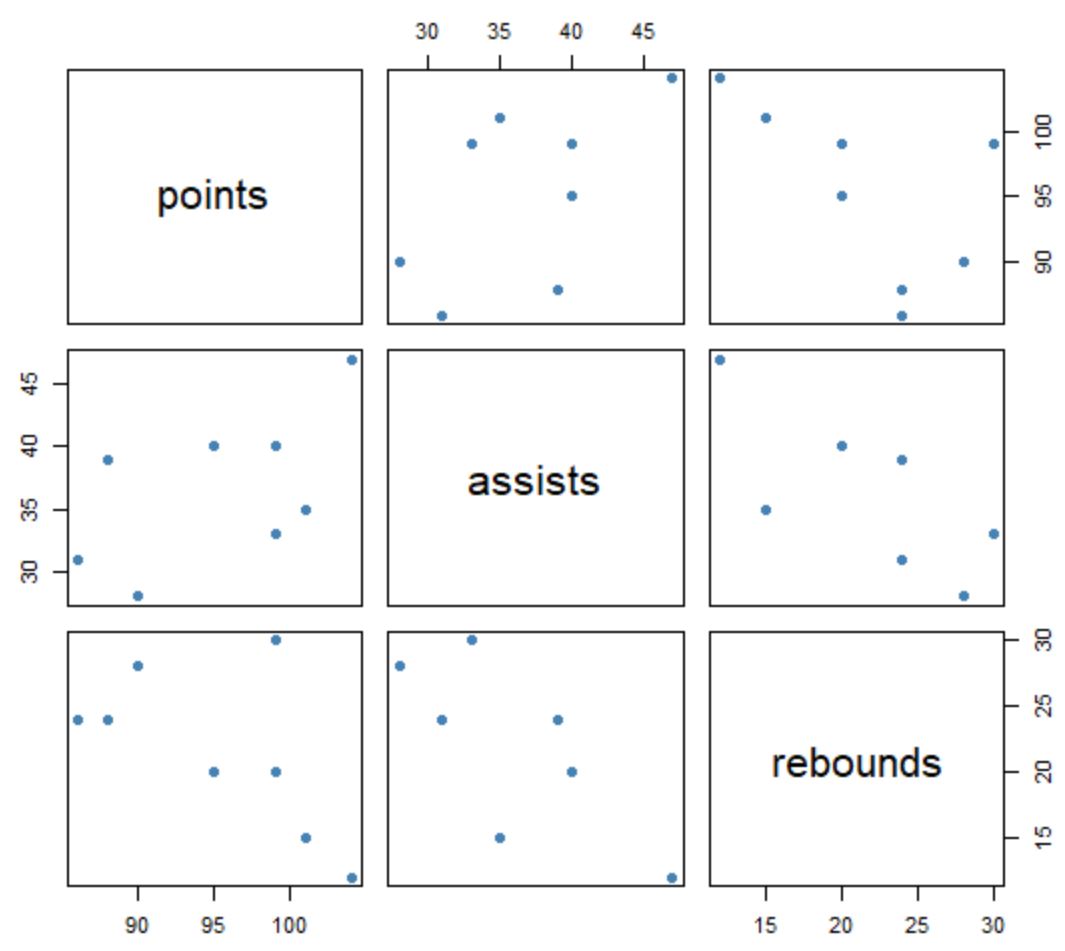
Способ интерпретации матрицы следующий:

• Имена переменных отображаются вдоль диагональных прямоугольников.
• Во всех остальных полях отображается диаграмма рассеяния взаимосвязей между каждой парной комбинацией переменных. Например, в поле в правом верхнем углу матрицы отображается диаграмма рассеяния значений очков и подборов . В средней левой области показана диаграмма рассеяния значений очков , передач и т. д.

Обратите внимание, что cex управляет размером точек пути, а col — цветом точек.

Пример 2. Создайте матрицу диаграммы рассеяния с помощью ggplot2 и GGally

Мы также можем использовать функцию ggpairs() из пакетов ggplot2 и GGally в R, чтобы создать матрицу диаграммы рассеяния для каждой переменной в нашем фрейме данных:

 library (ggplot2)
library (GGally)

#create scatterplot matrix
ggpairs(df) 

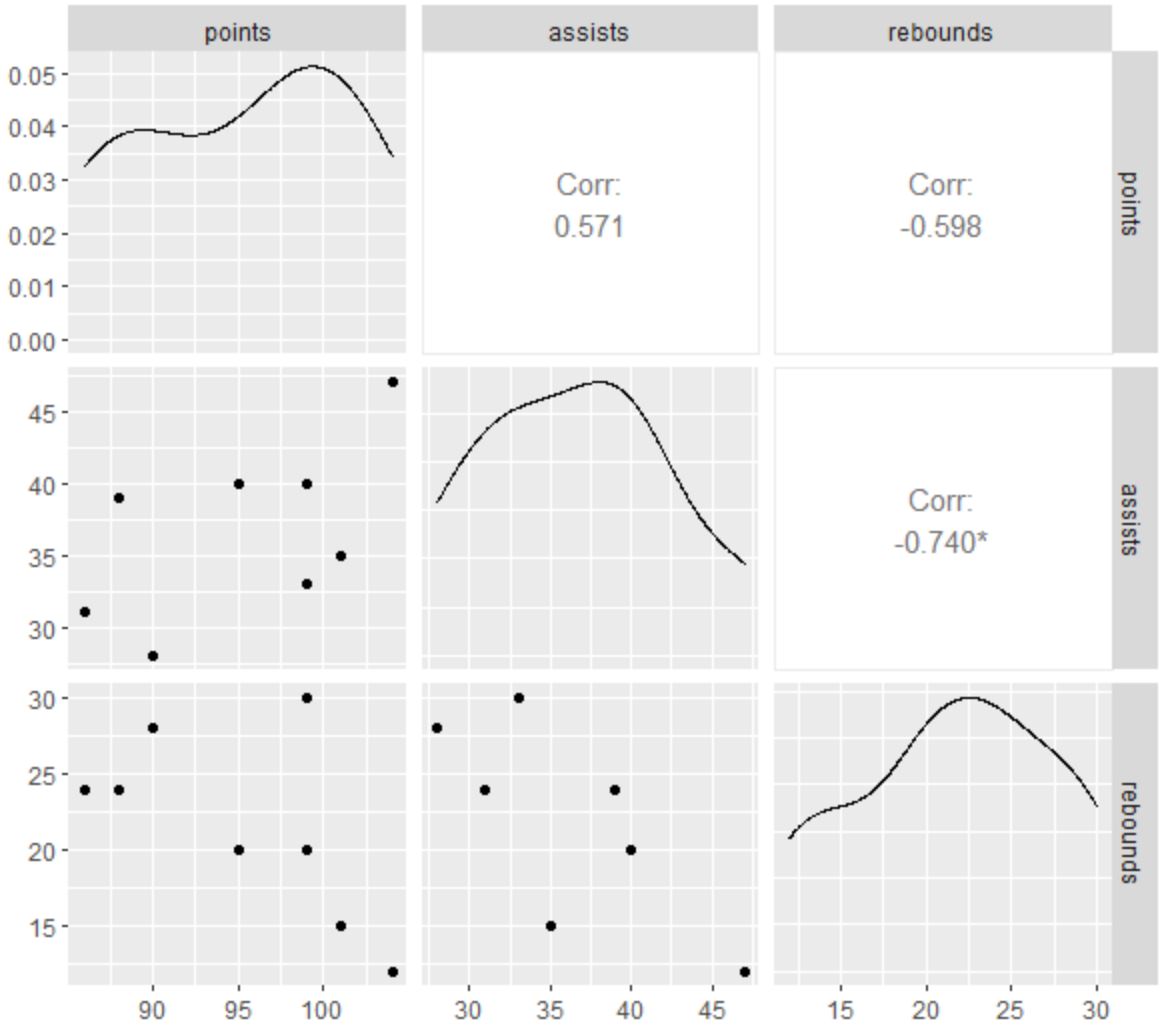
Эта матрица диаграммы рассеяния содержит те же диаграммы рассеяния, что и функция R baseplot() , но, кроме того, мы также можем видеть коэффициент корреляции между каждой парной комбинацией переменных, а также график плотности для каждой отдельной переменной.

Например, мы можем увидеть:

• Коэффициент корреляции между результативными передачами и очками составляет 0,571 .
• Коэффициент корреляции между подборами и очками составляет -0,598 .
• Коэффициент корреляции между подборами и передачами составляет -0,740 .

Маленькая звездочка ( * ) рядом с -0,740 также указывает на то, что корреляция между подборами и передачами статистически значима.

Дополнительные ресурсы

В следующих руководствах объясняется, как выполнять другие распространенные задачи в R:

Как создать корреляционную матрицу в R
Как создать облака точек по группам в R