Как найти медиану сгруппированных данных: с примерами

Мы часто хотим вычислить медиану данных, сгруппированных каким-либо образом.

Напомним, чтомедиана представляет собой значение, лежащее непосредственно в середине набора данных, когда все значения упорядочены от наименьшего к наибольшему.

Например, предположим, что у нас есть следующие сгруппированные данные:

Хотя вычислить точную медиану невозможно, поскольку мы не знаем значений необработанных данных , медиану можно оценить, используя следующую формулу:

Медиана сгруппированных данных = L + W[(N/2 – C) / F]

Золото:

• L : Нижний предел медианного класса.
• W : Средняя ширина класса
• N : Общая частота
• C : Совокупная частота до медианного класса.
• F : Медианная частота классов

Примечание . Средний класс — это класс, который содержит значение, расположенное по адресу N/2. В приведенном выше примере всего N = 23 значения. Таким образом, медианное значение равно значению в позиции 23/2 = 11,5, что соответствует классу 21-30.

В следующих примерах показано, как вычислить медиану сгруппированных данных в различных сценариях.

Пример 1. Вычисление медианы сгруппированных данных

Предположим, у нас есть следующее распределение частот, показывающее, что экзамен оценили 40 учеников определенного класса:

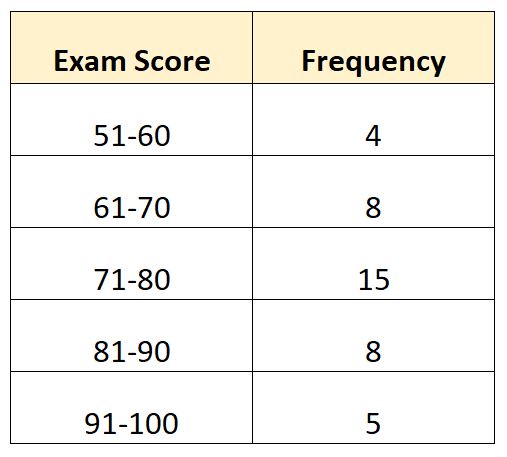
В этом примере всего N = 40 значений. Таким образом, медианное значение находится в классе, где находится 40/2 = 20. 20-е по величине значение будет находиться в классе 71–80 .

Зная это, мы можем рассчитать следующие значения:

• L : Предел нижнего среднего класса: 71.
• W : Средняя ширина класса: 9
• N : Общая частота: 40
• C : Совокупная частота до медианного класса: 12.
• F : Средняя частота классов: 15

Мы можем подставить эти значения в формулу для расчета медианы распределения:

• Медиана = L + W[(N/2 – C) / F]
• Медиана = 71 + 9[(40/2 – 12)/15]
• Медиана = 75,8

По нашим оценкам, средний балл на экзамене составляет 75,8 .

Пример 2. Вычисление медианы сгруппированных данных

Предположим, у нас есть следующее частотное распределение, показывающее количество очков, набранных за игру 60 баскетболистами:

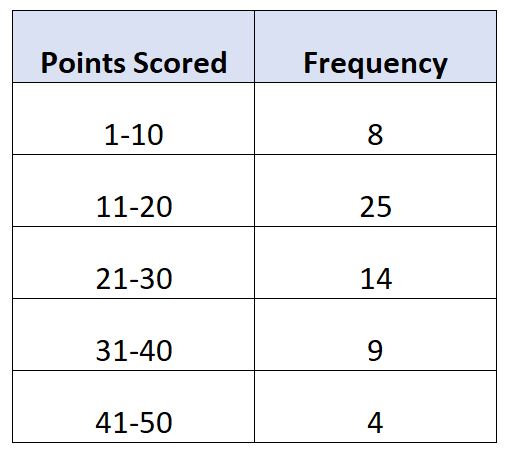
В этом примере всего N = 60 значений. Таким образом, медианное значение находится в классе, где находится 60/2 = 30. 30-е по величине значение будет в классе 11–20 .

Зная это, мы можем рассчитать следующие значения:

• L : Предел нижнего среднего класса: 11.
• W : Средняя ширина класса: 9
• N : Общая частота: 60
• C : Совокупная частота до медианного класса: 8.
• F : Средняя частота классов: 25

Мы можем подставить эти значения в формулу для расчета медианы распределения:

• Медиана = L + W[(N/2 – C) / F]
• Медиана = 11 + 9[(60/2 – 8)/25]
• Медиана = 18,92

По нашим оценкам, средний балл на экзамене составляет 18,92 .

Дополнительные ресурсы

В следующих руководствах объясняется, как выполнять другие распространенные операции с сгруппированными данными:

Как найти среднее и стандартное отклонение сгруппированных данных
Как найти режим сгруппированных данных
Как рассчитать процентильный рейтинг для сгруппированных данных