Влияют ли выбросы на межквартильный размах (iqr)?

В статистике мы часто хотим знать, насколько широко значения «разбросаны» в распределении.

Популярным способом измерения разброса является межквартильный размах , который рассчитывается как разница между первым и третьим квартилем набора данных. Квартили — это просто значения, которые делят набор данных на четыре равные части.

Пример: Расчет межквартильного размаха

В следующем примере показано, как рассчитать межквартильный размах для данного набора данных:

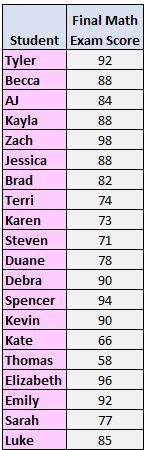
Шаг 1: Расположите значения от меньшего к большему.

58, 66, 71, 73, 74, 77, 78, 82, 84, 85, 88, 88, 88, 90, 90, 92, 92, 94, 96, 98.

2. Найдите медиану.

58, 66, 71, 73, 74, 77 , 78, 82, 84, 85, 88, 88, 88, 90, 90, 92, 92, 94, 96, 98.

В этом случае медиана находится между 85 и 88.

3. Медиана делит набор данных на две половины. Медиана нижней половины — это нижний квартиль, а медиана верхней половины — это верхний квартиль:

58, 66, 71, 73, 74 , 77, 78, 82, 84, 85, 88, 88, 88, 90, 90, 92, 92, 94, 96, 98 .

4. Рассчитайте межквартильный размах.

В этом случае первый квартиль — это среднее значение двух средних значений в нижней половине набора данных (75,5), а третий квартиль — среднее значение двух средних значений в верхней половине набора данных. (91).

Таким образом, межквартильный размах равен 91 – 75,5 = 15,5.

Межквартильный размах не зависит от выбросов

Одна из причин, по которой люди предпочитают использовать межквартильный диапазон (IQR) при расчете «разброса» набора данных, заключается в том, что он устойчив к выбросам. Поскольку IQR представляет собой средний диапазон 50% значений данных, на него не влияют экстремальные выбросы .

Чтобы продемонстрировать это, рассмотрим следующий набор данных:

[1, 4, 8, 11, 13, 17, 17, 20]

Вот различные метрики распространения для этого набора данных:

• Межквартильный размах: 11
• Диапазон: 19
• Стандартное отклонение: 6,26
• Разница: 39,23

Теперь рассмотрим тот же набор данных, но с добавлением экстремального выброса:

[1, 4, 8, 11, 13, 17, 17, 20, 150 ]

Вот различные метрики распространения для этого набора данных:

• Межквартильный размах: 12,5
• Диапазон: 149
• Стандартное отклонение: 43,96
• Спред: 1 932,84

Обратите внимание, что межквартильный размах меняется незначительно — от 11 до 12,5. Однако все остальные меры дисперсии резко изменяются.

Это демонстрирует, что выбросы не влияют на межквартильный размах, как на другие меры дисперсии. По этой причине это надежный способ измерить распределение средних 50% значений в любом распределении.

Дальнейшее чтение:

Измерения дисперсии
Калькулятор межквартильного диапазона